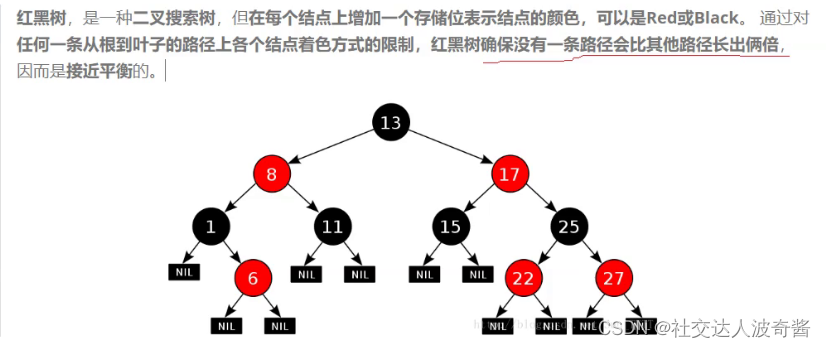
红黑树性质:
1.每个结点不是红色就是黑色。
2.根节点是黑色
3.如果一个节点是红色,它的两个孩子必须是黑色
4.对于每个节点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点
5.每个叶结点都是黑色的(此处的叶子结点指的是空结点)
6.红黑路径的计算从根结点到NIL结点(红黑树特殊的黑色结点)
7.红黑树路径节点个数计算,不包括叶节点
8.最长路径的节点个数不会超过最短路径节点个数的两倍
证明满足上述条件,最长路径的节点个数不会超过最短路径节点个数的两倍。
最长路径*1/2<=黑节点个数,最短路径的黑结点个数=最长路径黑结点个数,
最小路径>=黑节点个数>=最长路径*1/2。
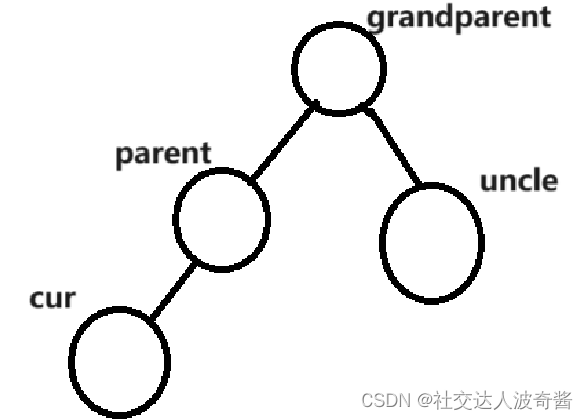
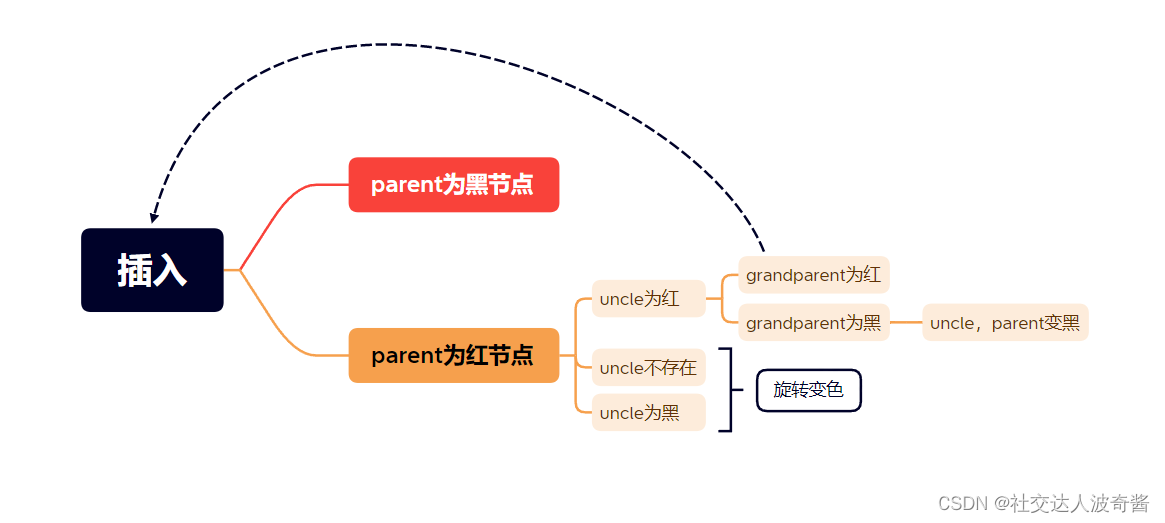
cur,parent,uncle为红,
grandparent再进行判断

cur,parent为红,uncle为黑或者uncle不存在
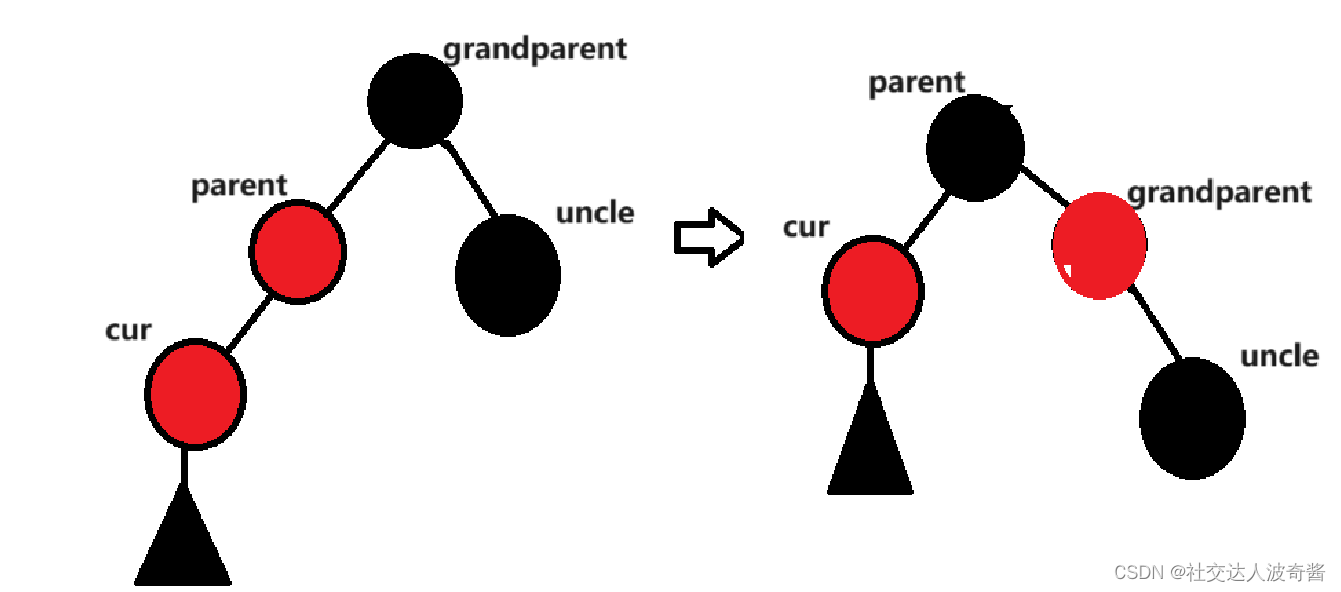

parent为黑,grandparent为红,三角型表示存在至少一个黑色节点来维持左右黑色节点数目平衡。
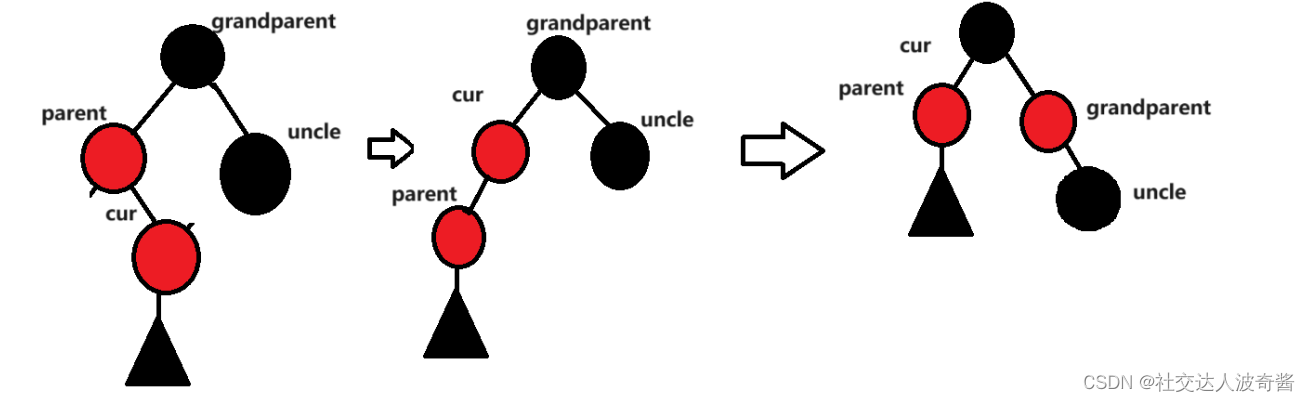
双旋,parent先左旋转,cur再右旋。
uncle不存在时同理
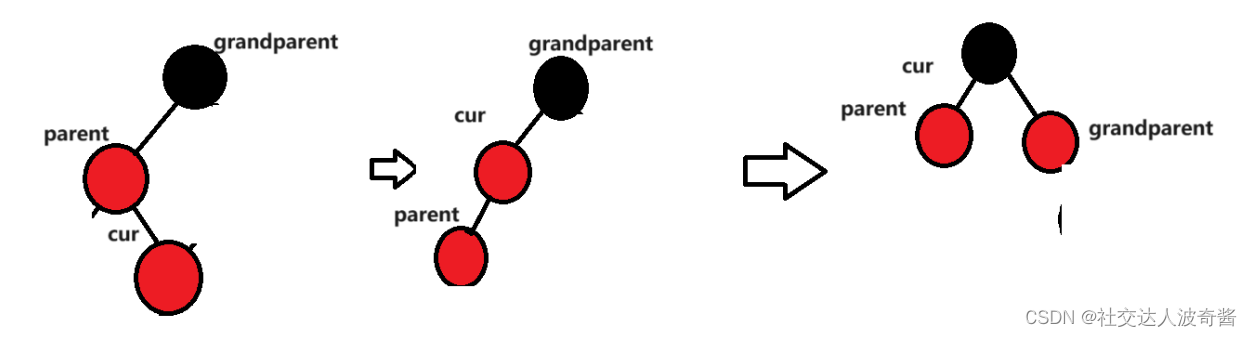
总结:同理左右单旋取决于cur在parent的哪一边 ,unle颜色决定是否旋转。
补充:uncle为黑时,cur必然不是新插入节点,原因为了维持左右黑节点数目平衡,cur下面必然还有其他节点。
分析:红黑树最重要的两个性质,红红不能相连,左右黑数目相同。当红红相连时,必然有其一变变黑,新增的黑色节点只能在根或者子树的根处来保持平衡,旋转的目的就是如此平衡左右黑节点。
代码如下:
enum Colour
{
RED,
BLACK
};
template<class K,class V>
struct RBTreeNode
{
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
pair<K, V> _kv;
Colour _col;
RBTreeNode(const pair<K,V>& kv)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
,_col(BLACK)
{}
};
template<class K,class V>
struct RBTree
{
typedef RBTreeNode<K, V> Node;
public:
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = BLACK;
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
cur->_col = RED;
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
if (parent==grandfather->_left)
{
Node* uncle = grandfather->_right;
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
}
else //u不存在或者存在且为黑
{
if (cur==parent->_left)
{
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
else
{
Node* uncle = grandfather->_right;
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
}
else //u不存在或者存在且为黑
{
if (cur == parent->_right)
{
RotateL(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
}
_root->_col = BLACK;
return true;
}void RotateL(Node* parent)
{
Node* cur = parent->_right;
Node* curleft = parent->_left;
parent->_left = curleft;
if (curleft)
{
curleft->_parent = parent;
}
cur->_left = parent;
Node* ppnode = parent->_parent;
parent->_parent = cur;
if (parent == _root)
{
_root = cur;
cur->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = cur;
}
else
{
ppnode->_right = cur;
}
cur->_parent = ppnode;
}
} void RotateR(Node* parent)
{
Node* cur = parent->_left;
Node* curright = cur->_right;
parent->_left = curright;
cur->_right = parent;
Node* ppnode = parent->_parent;
if (curright)
{
curright->_parent = parent;
}
parent->_parent = cur;
if (ppnode == _root)
{
_root = cur;
cur->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = cur;
}
else
{
ppnode->_right = cur;
}
}
}
bool CheckColour(Node* root,int blacknum,int benchmark)
{
if (root == nullptr)
{
if (blacknum > 2 * benchmark)
{
return false;
}
return true;
}
if (root->_col == BLACK)
{
++blacknum;
}
if (root->_col == RED && root->_parent && root->_parent->_col == RED)
{
cout << root->_kv.first << "出现连续红色节点" << endl;
return false;
}
return CheckColour(root->_left,blacknum,benchmark)
&& CheckColour(root->_right,blacknum,benchmark);
}
bool IaBalance()
{
IsBalance(_root);
}
bool IsBalance(Node* root)
{
if (root == nullptr)
return true;
if (root->_col != BLACK)
{
return false;
}
//基准值
int benchmark = 0;
Node* cur = _root;
while (cur)
{
if (cur->_col == BLACK)
{
++benchmark;
}
cur = cur->_left;
}
return CheckColour(root,0,benchmark);
}