【LeetCode力扣】LCR170 使用归并排序的思想解决逆序对问题（详细图解）

news2024/11/17 17:50:07

1、题目介绍

2、解题思路

2.1、暴力破解法

2.2、归并排序思想

2.2.1、画图详细讲解

2.2.2、归并排序解决逆序对的代码实现

1、题目介绍

首先阅读题目可以得出要点，即当前数大于后数时则当作一个【逆序对】，而题目是要求在一个数组中计算一共存在多少个这样的逆序对并输出结果。

原题链接：LCR 170. 交易逆序对的总数 - 力扣（LeetCode）

2、解题思路

2.1、暴力破解法

看到这里的第一反应就是这不是很简单吗？心想着这困难题也不过如此吧（笑）。

就是直接使用暴力破解法，只需要两个for循环嵌套，一个record[ i ]在原地，另一个record[ j ]将后面所有遍历一遍，只要比record[ i ]的小就将计算器count加1，然后i++再从头遍历，知道找完所有，最后返回计数器count即可，于是便奋笔疾书写了起来。

int reversePairs(int* record, int recordSize) {
	if (recordSize == 0)
	{
		return 0;
	}
	int count = 0;
	int i = 0, j = 0;
	for (i = 0; i < recordSize - 1; i++)
	{
		for (j = i + 1; j < recordSize; j++)
		{
			if (record[i] > record[j])
			{
				count++;
			}
		}
	}
	return count;
}

当写完然后测试了简答数据无误，然后自信满满地点击提交，结果却直接被打脸。

看了报错结果才恍然大悟，看题目时漏看了数组长度。

题目设置的数组长度最长可达 50000，因此使用暴力破解法虽然非常简单，但是时间复杂度也非常大为O(n^2)，这肯定会超出时间限制的。因此需要使用一种时间复杂度较小的遍历。到了这里才终于理解了这道题为什么是困难题！！！

2.2、归并排序思想

这里思考了一下，只要能找到一种时间复杂度低，并且通过比较排序的算法，在比较排序的过程中顺便进行记录，这样的化就能够解决这个问题了。

于是归并排序便浮现在眼前，归并排序的时间复杂度很低只有O(nlogn)，并且也是通过比较的方式进行排序，那么只需要在传统的归并排序算法中添加一些用于记录前者大于后者计算器即可。

简单回顾一下归并排序的知识：

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用递归或者说是分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序，它包含这样三个步骤：

分解：把长度为n的待排序序列分成两个长度为n/2的子序列。例如L代表头部，M代表中点，R代表尾部，将[ L，R ]分成[ L，M ]和[ M+1，R ]。
解决：使用归并排序递归地排序两个子序列。
合并：将两个排序好的子序列[ L，M ]和[ M+1，R ]合并成一个最终的排序序列。

在待排序序列长度为 1 的时候，递归开始「回升」，因为我们默认长度为 1 的序列是排好序的。简单来说就是：当分到单个子序列只剩下一个数字时，一个数字就是天然了有序，即此时左侧和右侧都排好序了，然后递归进行回升操作。

由于篇幅原因，如果想要更加详细地了解有关归并排序的知识，可以前往往期博客中阅读：

【算法与数据结构】归并排序的代码实现（详细图解）以及master公式的讲解_Hacynn的博客-CSDN博客https://blog.csdn.net/zzzzzhxxx/article/details/133516177?spm=1001.2014.3001.5501

2.2.1、画图详细讲解

假设我们通过归并排序的「回升」操作已经得到了两个已排序的子序列并等待合并，这两个子序列假设为：左子序列[ 8,15,17,22,35 ]和右子序列[ 9,12,15,30,38 ]。然后用malloc开辟辅助数组help，并定义一个变量sum用于记录当前逆序对的个数。

一开始我们先用p1指向左子序列的头部，p2指向右子序列的头部，i指向help数组的头部。

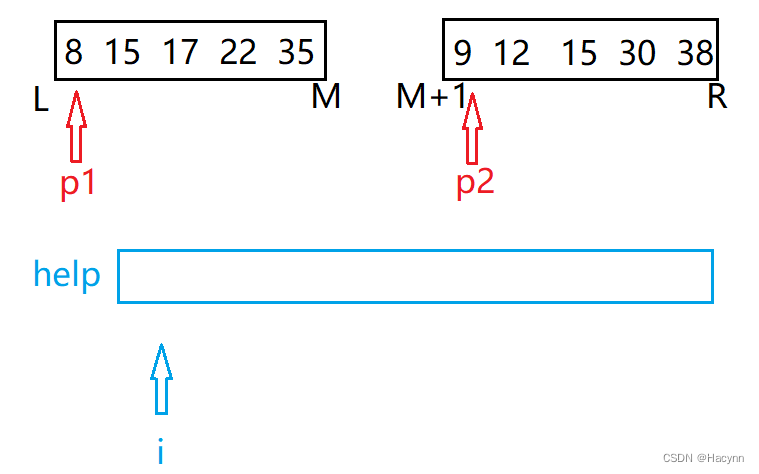
此时开始比较p1和p2指向的值，我们发现p1小于p2，不符合逆序对的前者大于后者，因此不做其他操作，直接将值放入help数组 i 位置中，并且分别进行p1++和i++，使指向下一个元素。

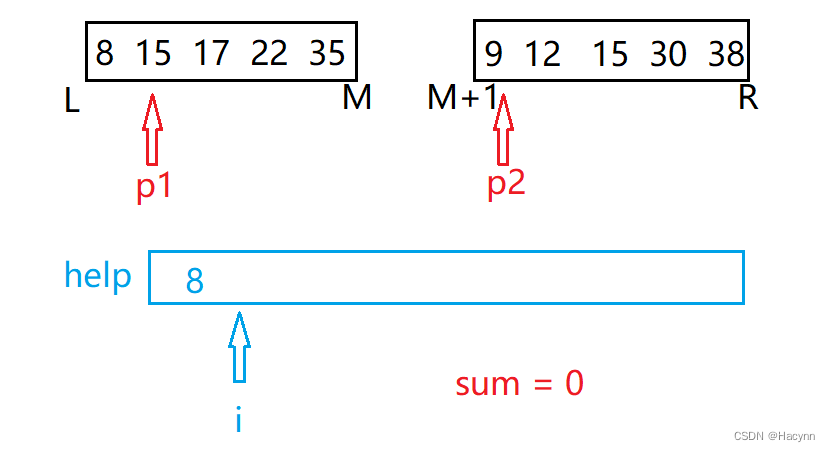
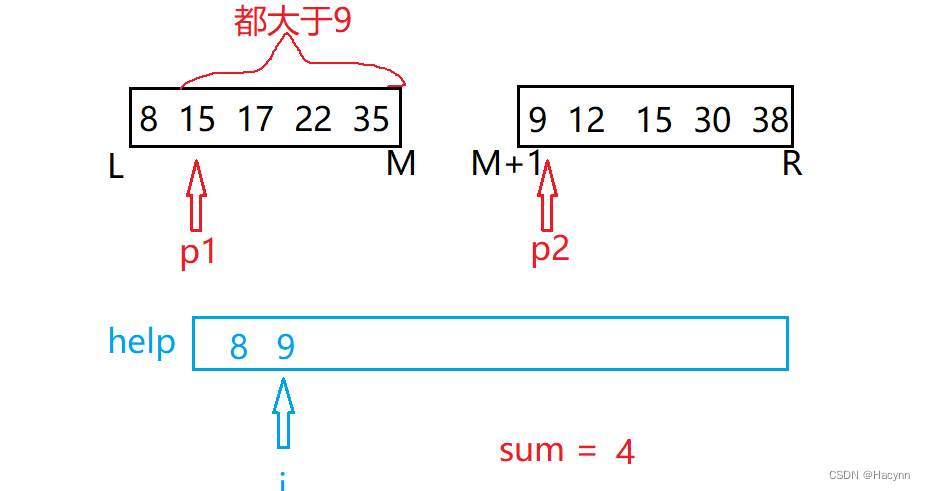
重复p1和p2的比较操作，发现此时p1大于p2，此时记录逆序对的sum本应该自增1。

但是这里我们可以发现一个规律：因为左子序列是有序的，如果p1此时的数比p2大，那就证明p1后面的数字也依然比p2大，因此逆序对应该有M-p1+1即4个，分别是：(15，9)、(17，9)、(22，9)、(35，9)。

所以此时sum应该+4，并将p2所指的较小值存入help中。

i++、p2++；

此时p1仍然大于p2，再次使用M-p1+1计算出逆序对为4个，分别是(15,12)、(17,12)、(22,12)、(35,12)。

此时 sum = sum+4，并将12存入help中。

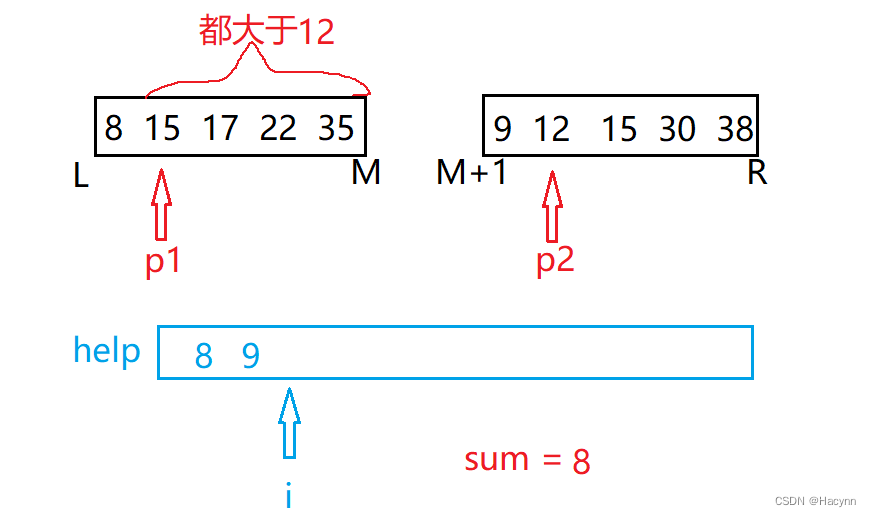
i++，p2++；

注意特殊：此时p1 == p2，该算法在等于时尤为关键，当相等时应该将左侧p1的15放入help中并p1++，如果放的是右侧p2的15存入，就会丢失一部分逆序对，这个原理读者可以自己画图理解。

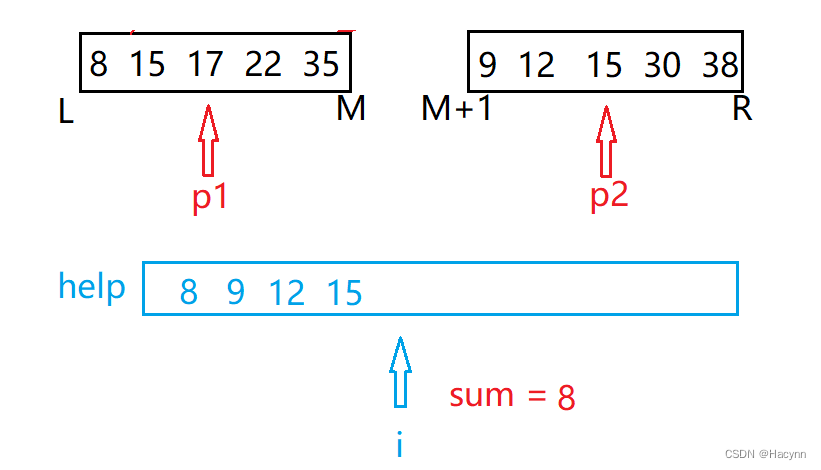
剩下的部分依然按照此规律进行操作，最终算出该轮遍历的逆序对数sum。

2.2.2、归并排序解决逆序对的代码实现

int ExternalSort(int* arr, int L, int M, int R)
{
	int* help = (int*)malloc(sizeof(int) * (R - L + 1));
	int p1 = L;
	int p2 = M + 1;
	int sum = 0;
	int i = 0;
	while ((p1 <= M) && (p2 <= R))
	{
        //p1 大于 p2 则计算出逆袭对个数并加入sum中，p1小于p2时则给0（即不操作）
		sum += arr[p1] > arr[p2] ? (M - p1 + 1) : 0;
        //较小的数拷贝进help数组，相等时拷贝p1指针的数
		help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
	}
    //当有一个子序列遍历完了，则将另外一个子序列中剩余的数据全部放入help数组中
	while (p1 <= M) { help[i++] = arr[p1++]; }
	while (p2 <= R) { help[i++] = arr[p2++]; }
    //将辅助数组help中已经合并完成的数据传回给原数组arr的相应位置
	for (i = 0; i < (R - L + 1); i++)
	{
		arr[L + i] = help[i];
	}
	free(help);
	help = NULL;
	return sum;  //返回本轮操作的sum值

}

int MergeSort(int* arr, int L, int R)
{
	if (L == R)
	{
		return 0;
	}
	int mid = L + (R - L) / 2;
	return MergeSort(arr, L, mid) +   //对拆分的左子序列进行递归操作
		MergeSort(arr, mid + 1, R) +  //对拆分的右子序列进行递归操作
		ExternalSort(arr, L, mid, R);  //外部排序并计算出逆序对sum
}

int reversePairs(int* record, int recordSize) {
	int ret = 0;
	if (recordSize == 0)    //对空数组进行判断
	{
		return 0;
	}
	ret = MergeSort(record, 0, recordSize - 1);
	return ret;
}