一、雷达测距原理

1.1 基本原理

我们知道，电磁波的传播速度为光速 $c$，若雷达与目标之间的距离为 $R$，则雷达发出的电磁波到达目标，再经过目标反射后被雷达接收到，所用的时间 $\tau$ 为：
$$\tau =\frac{2R}{c}$$
时间 $\tau$ 称为发射信号与回波信号的时延，对于LFMCW雷达，在一个调制周期内，发射信号与接收信号的差频 $f_b$ 为：
$$f_b=\mu \tau$$
进而可以得到：$f_b=\mu \frac{2R}{c}$，说明目标与雷达之间的相对距离 $R$ 跟信号混频后的差频 $f_b$ 成正比。
一般情况下，雷达的调频斜率 $\mu$ 是固定的，电磁波在空气中的传播速度 $c$ 约为$3\times 10^8$，所以要测量目标的距离 $R$，只需要计算差频 $f_b$ 即可。

1.2 实现方法

发射信号与接收信号经过混频、低通滤波等处理后，得到中频信号(IF)，此时的中频信号为模拟信号，需要用ADC将模拟信号转换为数字信号，才可以进行后续处理。ADC采样后的信号为离散点，借助离散傅里叶变换(DFT)，将中频信号从时域变换到频域，从而计算出信号的频率。

在实际工程应用中，为了计算的实时性，通常采用离散傅里叶变换的快速算法——快速傅里叶变换(FFT)来实现信号的时频转换。

1.3 与距离有关的概念

（1）最大测量距离
设中频信号的频率为 $f_{IF}$，$f_{IF}=f_b=\mu \frac{2R}{c}$，所以目标的最大可测量距离为：
$$R_{max}=\frac{f_{I{F}_{max}}c}{2\mu }$$
而信号经过ADC采样后，可测量的信号最大频率受限于采样率 $F_s$，即 $F_s>=f_{I{F}_{max}}=\mu \frac{2R_{max}}{c}$，从而得到：
$$R_{max}=\frac{F_{s}c}{2\mu }$$
实际上，无论是奈奎斯特采样还是带通采样，采样后可测量到有效的信号最大频率小于等于$F_s/2$。

（2）距离点精度
距离点精度表示在频域上，一个频率点(频率分辨率)对应的目标距离，设中频信号的采样点为 $N$，进行 $FFT$ 的点数为 $N_{fft}$，此时的频率分辨率为 $△f=\frac{F_s}{N_{fft}}$，从而得到距离点精度为：
$$R_{point}=\frac{c}{2\mu }\frac{F_s}{N_{fft}}$$
（3）距离分辨力
距离分辨率是指雷达对距离相近的两个目标的分辨能力。设两个目标与雷达之间的距离差为 $△R$，则在频域上其频率相差为 $△f=\frac{△R\cdot 2\mu }{c}$。
$$△f＞\frac{1}{T}=>\frac{△R\cdot 2\mu }{c}＞\frac{1}{T}=>△R>\frac{c}{2\mu \cdot T}$$
又因为带宽 $B=\mu \cdot T$，所以 $△R＞\frac{c}{2B}$，因此，距离分辨率的计算公式为：
$$R_{point}=\frac{c}{2B}$$
由距离点精度的计算公式易知，若信号进行 $FFT$ 的点数 $N_{fft}=N=F_s\cdot T$，则有 $△R=\frac{c}{2B}$

（4）距离测量精度
距离测量精度是指雷达对目标的距离测量值与目标到雷达的真实距离之间的误差。噪声是影响雷达测量的最主要因素，通常采用测量值与真实值之差的均方根值来度量雷达的测距误差，即测距精度。
计算公式为：
$${\sigma }_R=\frac{c}{2B\cdot sqrt(2SNR)}$$

二、MATLAB仿真实验

2.1 应用案例

（1）对固定目标的测量
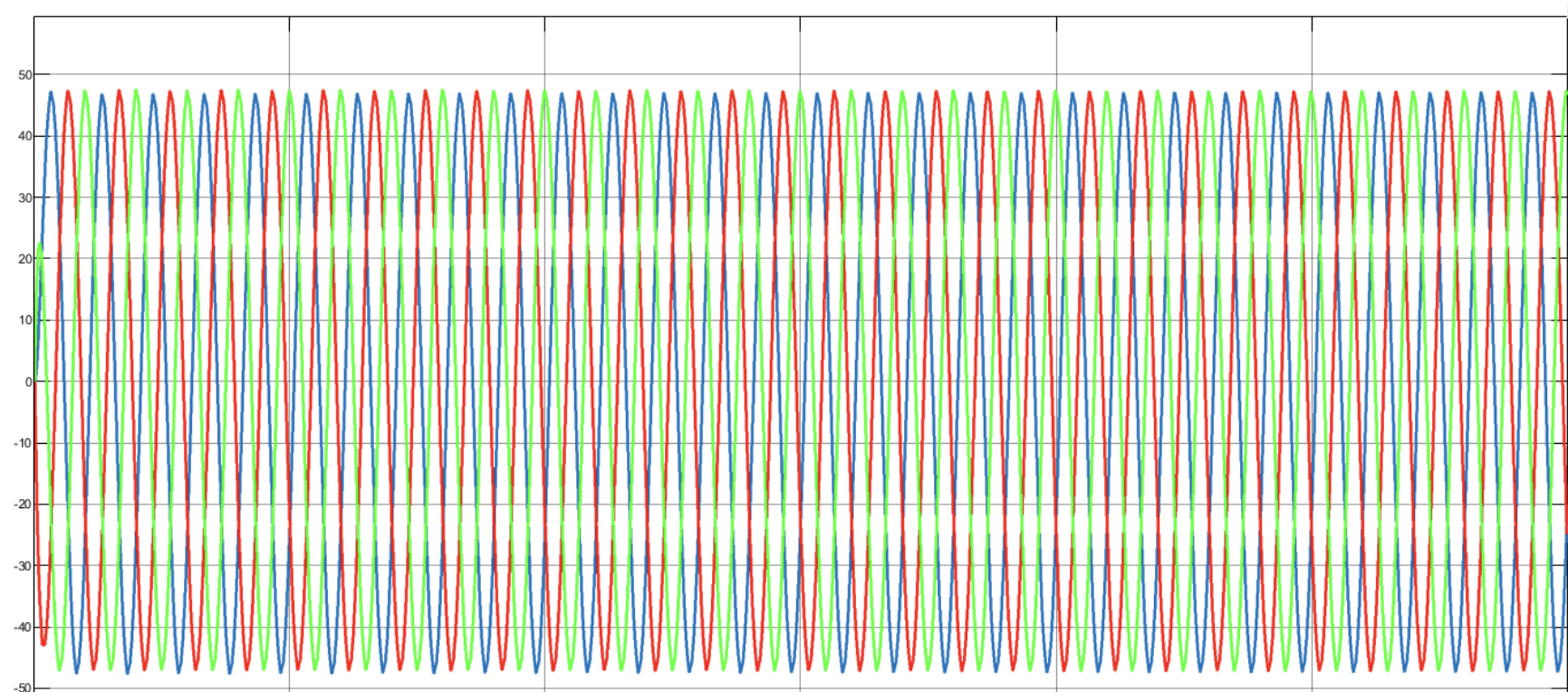
设定一个距离为R1=1000m的目标，利用雷达测距方法在MATLAB上进行仿真验证，对混频后的信号加汉明窗，进行4096点FFT，得到其频谱图如下：

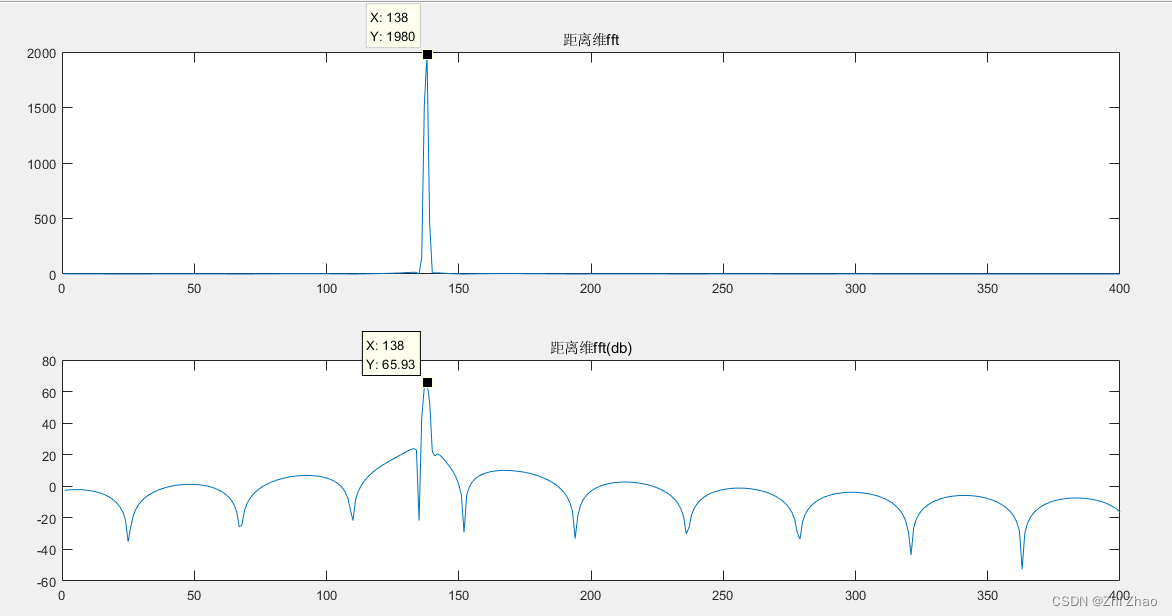
由图可知，目标峰值点出现在x=138的位置，根据距离点精度的计算公式 $R_{point}=\frac{c}{2\mu }\frac{F_s}{N_{fft}}$，得到 $R_{point}=7.3192$，所以目标距离测量结果为：
$$R_{me}=R_{point}\ast (138-1)=1002.7m$$
与目标实际位置1000m，存在2.7m的测距误差。

（2）不同带宽下的距离分辨率

2.2 MATLAB代码

（1）对固定目标的测量

clc;
clear;
close all;

%% LFM信号参数
B = 20e6;       % 带宽
T = 100e-6;      % 脉冲宽度
u = B/T;        % 调频斜率
fs = 2*B;       % 采样率
N = T*fs;       % 采样点数

c = physconst('LightSpeed');        % 光速
f0 = 77e9;                          % 载频
Lambda = c/f0;                      % 波长

R_max = fs*c/(2*u);     % 最大测量距离
%% 模拟信号
t = linspace(0,T,N);
Phase_t = @(f0,u,t) 2*pi*(f0*t+1/2*u*t.^2);        % LFM信号的相位表达式

Signal_Tx = rectpuls(t-T/2,T).*exp(1j*Phase_t(f0,u,t));        % 发射信号

R0 = 1000;           % 静止目标
tao = 2*R0/c;       % 目标回波的时延
Signal_Rx = rectpuls(t-T/2,T).*exp(-1j*Phase_t(f0,u,(t-tao)));        % 接收信号

% 混频
Signal_Mix = Signal_Tx.*Signal_Rx;

% 测距
win = hamming(N);       % 加窗
Nfft = 4096;            % FFT点数
R_point = (fs/Nfft)*c/(2*u);    % 距离点精度
delta_R = c/(2*B);              % 距离分辨率
fft_Data = fft(Signal_Mix.*win',Nfft);
figure;
subplot(2,1,1);plot(abs(fft_Data));title('距离维fft');xlim([0 400]);
subplot(2,1,2);plot(mag2db(abs(fft_Data)));title('距离维fft(db)');xlim([0 400]);

（2）不同带宽下的距离分辨率