T1：跳石板
 

[小易来到了一条石板路前，每块石板上从1挨着编号为：1、2、3.......
这条石板路要根据特殊的规则才能前进：对于小易当前所在的编号为K的 石板，小易单次只能往前跳K的一个约数(不含1和K)步，即跳到K+X(X为K的一个非1和本身的约数)的位置。 小易当前处在编号为N的石板，他想跳到编号恰好为M的石板去，小易想知道最少需要跳跃几次可以到达。
例如：
N = 4，M = 24：
4->6->8->12->18->24
于是小易最少需要跳跃5次，就可以从4号石板跳到24号石板

 

从n开始，求出n的所有约数xi(根号n的复杂度)，对于n能跳到n+xi，对该状态转移，方程是：

f[n+xi]=min(f[n+xi],f[n]+1) 然后对于n+1到m重复此算法。

时间复杂度：O（n*sqrt(n))

#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
const int N=1e5+10,INF=0x3f3f3f3f;
int f[N];
int n,m;
vector<int> fun(int x)
{
	vector<int>ans;
	for(int i=2;i*i<=x;i++){
		if(x%i==0){
			ans.push_back(i);
			if(i!=x/i){
				ans.push_back(x/i);
			}
		}
	}
	
	return ans;
}
int main()
{
	cin>>n>>m;
	memset(f,0x3f,sizeof(f));//初始化 0x3f3f3f3f是正无穷
	f[n]=0;
	for(int i=n;i<=m;i++){
		if(f[i]!=INF){
			vector<int>ans=fun(i);//求约数
			for(int x:ans){
				if(i+x<=m){
					f[i+x]=min(f[i+x],f[i]+1);
				}
			}
		}
	}
	if(f[m]==INF)cout<<-1<<endl;
	else cout<<f[m]<<endl;
	return 0;
}

T2：参数解析

链接：参数解析__牛客网

题目描述：

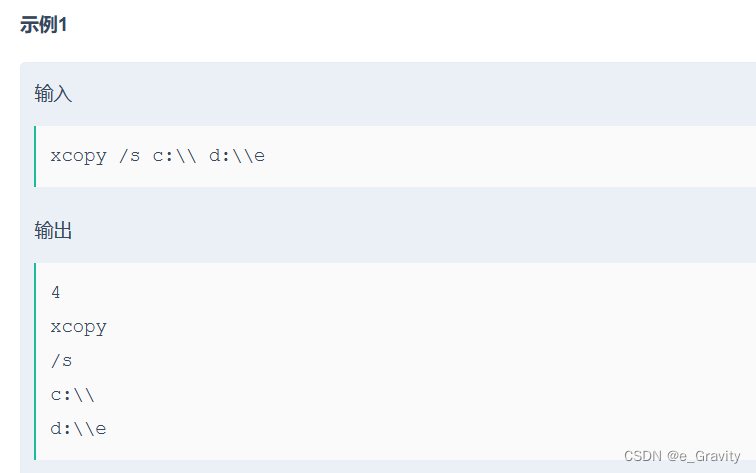
在命令行输入如下命令：

xcopy /s c:\\ d:\\e，

各个参数如下：

参数1：命令字xcopy

参数2：字符串/s

参数3：字符串c:\\

参数4: 字符串d:\\e

请编写一个参数解析程序，实现将命令行各个参数解析出来。

解析规则：

1.参数分隔符为空格
2.对于用""包含起来的参数，如果中间有空格，不能解析为多个参数。比如在命令行输入xcopy /s "C:\\program files" "d:\"时，参数仍然是4个，第3个参数应该是字符串C:\\program files，而不是C:\\program，注意输出参数时，需要将""去掉，引号不存在嵌套情况。
3.参数不定长

4.输入由用例保证，不会出现不符合要求的输入

数据范围：字符串长度：1≤s≤1000 

进阶：时间复杂度：O(n) ，空间复杂度：O(n) 

模拟题，注意读入用getline

#include<iostream>
#include<vector>
#include<string>
using namespace std;
vector<string>ans;
string s;
int main()
{
    getline(cin,s);
    s+=" ";
	bool flag=0;
	string temp;
	for(int i=0;i<s.size();i++){
		if(s[i]==' '&&!flag){
			ans.push_back(temp);
			temp="";
		}
		else if(s[i]=='"'){
            if(!flag) flag=1;
			else flag=0;
		}
		else temp+=s[i];
	}
	cout<<ans.size()<<endl;
	for(auto x:ans){
		cout<<x<<endl;
	}
    return 0;
}