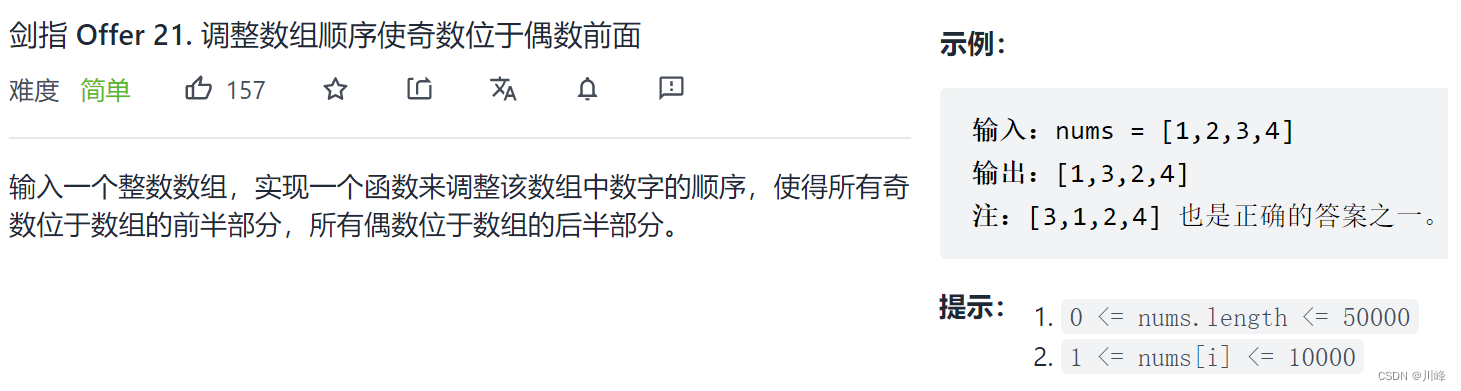
剑指 Offer 21.调整数组顺序使奇数位于偶数前面

• 对撞指针 ， 从左边不停的找第一个偶数，从右边不停的找第一个奇数 ，找到后 交换 两者位置

本题与【905. 按奇偶排序数组】几乎雷同。

剑指 Offer 57.和为s的两个数字

本题与【167. 两数之和 II - 输入有序数组】相同

• 1） 对撞指针 ，计算  sum(L + R)  的和，判断与  target  的关系，来决定移动左指针还是右指针
• 2） 二分查找 ，先固定一个  nums[i] ，然后到剩余数组 [ i+1...end ] 中二分查找  target = s - nums[i]  的值
• 注意：题目数组是 递增排序 好的，所以才能用上面两种方法，并且只要找到一个解即可返回。

 

26.删除有序数组中的重复项

• 1) 快慢指针 ， slow 指向 已处理区域 的 最后一个位置 ， fast 指向 未处理区域 的 第一个位置 ，初始 slow = 0, fast = 1，不断向后移动 fast
• 若 fast 的值跟 slow 的值 不等 ，就让 slow++ ，把 fast 处的值放到 slow 位置，最后返回 slow + 1  作为 数组长度 。 
• 注意：本题能这样做的原因是因为题目的数组是 升序排列 的。

 

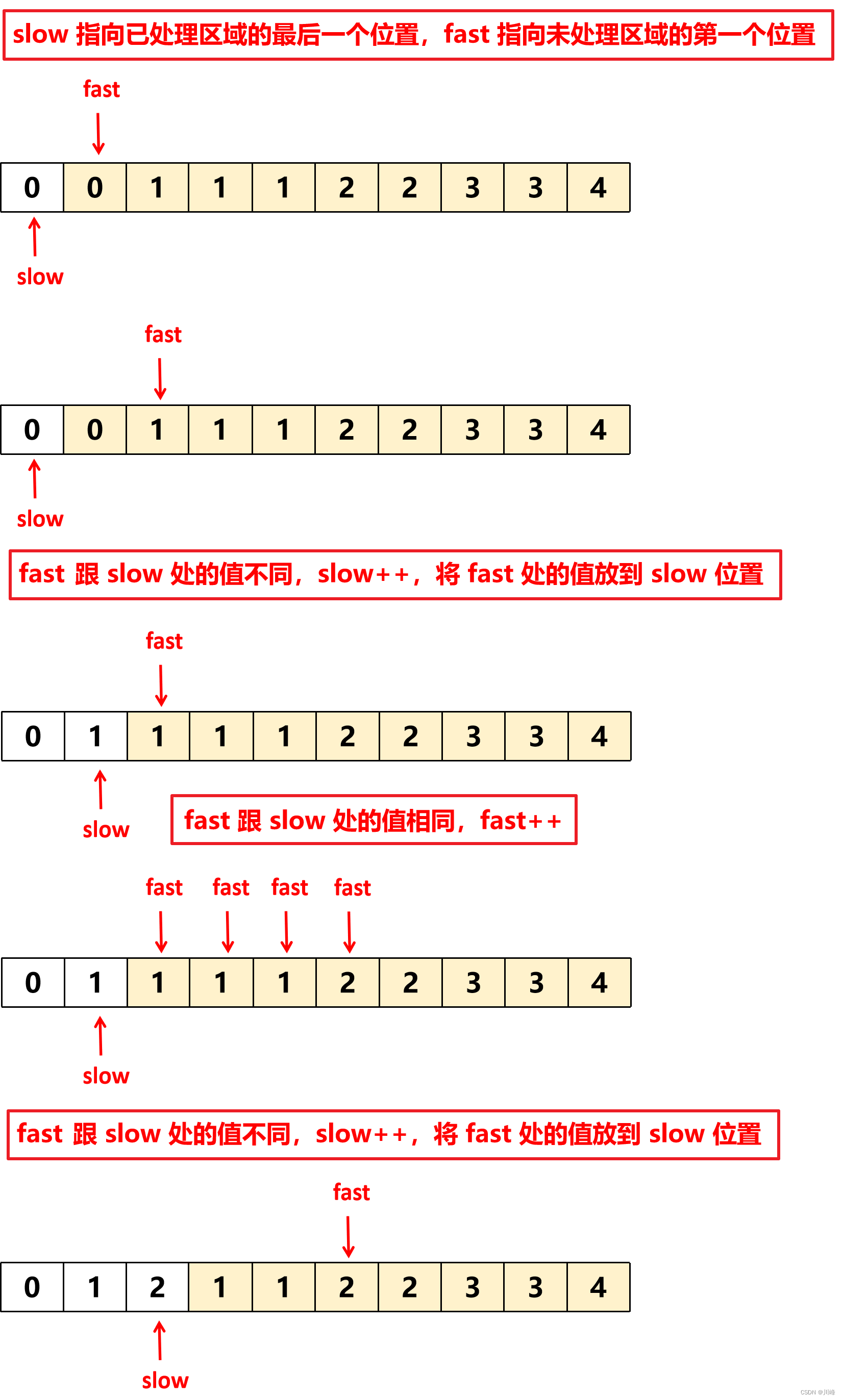
这种算法是不断比较未处理区域的值和已处理区域的最后一个值，由于数组是升序排列的，所以只需要跳过那些与已处理区域最后一个相同的值即可。然后只将不同的值往前面放。 

 

• 2) 快慢指针 ， slow 指向 已处理区域 的 下一个位置 ， fast 指向 未处理区域 的 第一个位置 ， 初始 slow = 1, fast = 1 ，不断向后移动 fast
• 若 fast 的值跟 fast-1 不同时，就把 fast 处的值放到 slow 位置，然后 slow++ ， 最后返回 slow 作为 数组长度 。 
• 注意：本题能这样做的原因是因为题目的数组是 升序排列 的。

 

这种算法是不断比较未处理区域的当前值和上一个值，由于数组是升序排列的，所以只需要跳过那些与上一个相同的值即可。然后只将不同的值往前面放。 

问题：为什么 slow 和 fast 要从 1 位置开始呢？

这是因为 slow 的含义是已处理区域的下一个位置，初始时，前面预留的 0 位置表示该位置默认是已经被处理的区域，即 1 个数字本身是不重复的，所以 slow 从 0 位置的下一个位置开始。而 1 位置表示未处理的第一个位置，所以 fast 从 1 位置开始。在方法 1 中 slow 从 0 开始的含义也是一样的，表示此时 0 位置是已处理的最后一个位置（同时也是已处理的第一个位置）。

 

• 类似26， slow 指向 已处理区间 的 下一个位置,   slow 前面 预留两个空位 ,  slow、fast 从第 3 个元素开始，即初始 slow = 2, fast = 2 ,   不断向后移动 fast
• 若 fast 跟 slow - 2 位置的元素不同，就把 fast 处的值放到 slow 的位置，然后 slow++ ， 最后返回 slow 作为数组长度。
• 注意：本题能这样做的原因是因为题目的数组是 有序排列 的。

 

 

这里之所以前面预留2个空位，是因为题目要求重复元素只出现2次，因此如果前两个元素重复也没有关系，如果前两个元素不同，更没有问题。

还有一个问题是为什么跟 fast 比较的是 slow - 2 位置的数呢？

如果 fast 跟 slow - 2 相同，而 slow - 2 又可能与 slow - 1 相同，那么就有可能出现三个相同的数： nums[fast] == nums[slow - 2] == nums[slow - 1]，此时重复元素出现次数 > 2 了，因此 fast 必须跟 slow - 2 保持不同，这样重复元素最多出现 2 次。

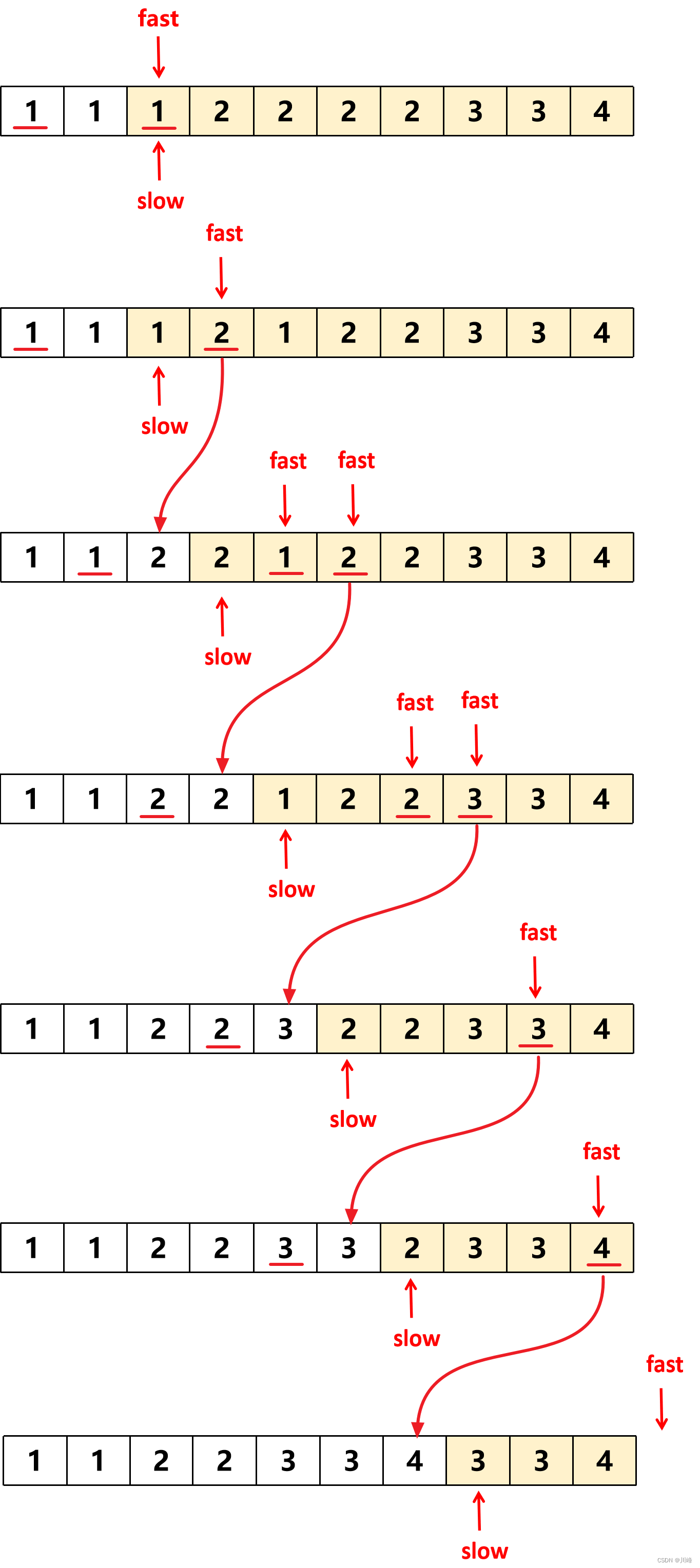
那如果 fast 跟 slow - 1 比较不同时就赋值，这样行不行呢？如下图所示，这样会完美的错过后面所有重复数字的答案（重复的2和3只保留了一个）

 

287. 寻找重复数

• 1）快慢指针，存在重复数字的数组会形成环，类似141环形链表， 环的入口处即重复元素 ，
• 将题目给的数组当作 一个数组形式的链表 来看待，数组的下标就是指向元素的指针，把数组的元素也看作指针。
• 例如 0 是指针，指向 nums[0] ，而 nums[0] 也是指针，指向 nums[nums[0]] 。
• slow 和 fast 初始为 0 ，然后 slow 走一步， fast 走两步，如果 slow 追上 fast 就退出循环， 此时让 slow = 0 回到开头，然后 slow 和 fast 同步走，如果 slow 追上 fast , 则相遇点就是重复数字。 

看一下为什么题目给定的存在重复数字的数组会形成环： 

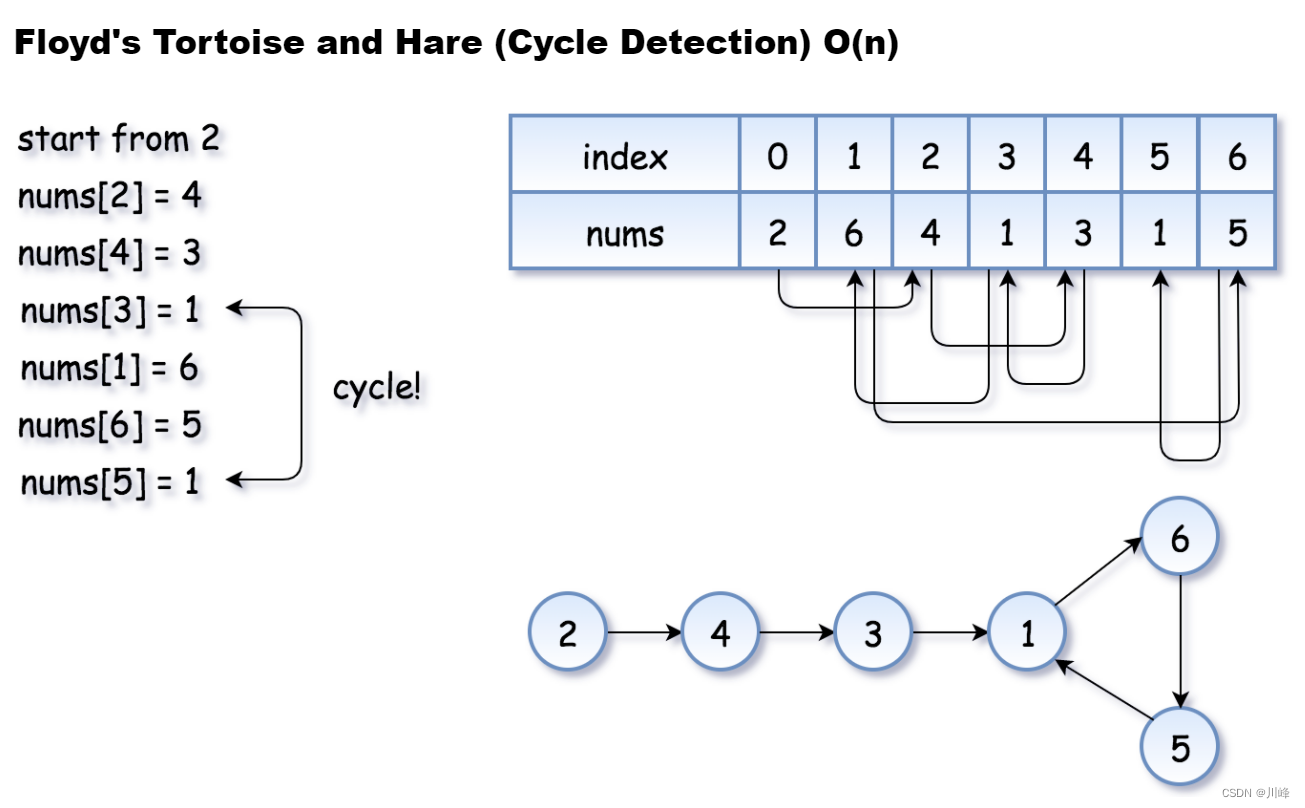
如上图所示：我们使用函数 f(x) = nums[x] 来建立一个数列：x，nums[x]，nums[nums[x]]， nums[nums[nums[x]]]...... 即每一个数的位置是前一个数的值，如果我们从 x＝nums[0] 开始，又因为 nums 里有一个重复的数字，这必将形成一个带有循环的数列。

更复杂的例子／更大的圈：

我们不难看出，进入循环的点就是我们要找的重复的数字（即上面两个例子里的 1 和 9），问题是如何找到它？答案就是使用快慢指针。

• 2） 二分查找 ， 在  [1, n] 数字区间上二分， 对于 mid = (L + R) / 2 ，重复的数要么落在 [L, mid]  要么落在 [mid + 1, R] ，
• 每次二分后统计数组中 ≤ mid  的元素的个数 count ，然后根据 count 和  mid  的大小关系来决定接下来到哪边去二分：
• ① 如果 count ≤ mid ，说明左边没有重复，收缩左边界 L = mid + 1 ，到右半边区间 [mid + 1, R] 查找；
• ② 如果 count  >  mid ，说明 [L, mid] 内出现了重复元素， 收缩 R 到 mid - 1 ，到左半边区间 [L, mid - 1] 继续查找，但是此时需要用变量 res 记录一下移出的 mid 值，因为它可能是潜在的重复元素。最后返回 res 即可。

为什么二分时要统计 ≤ mid 的元素个数呢？

简单的来说就是一个萝卜一个坑，mid 及左侧最多有 mid 个坑（如果包含1~n连续不重复的话），如果出现了重复元素，就可能超过 mid 个坑。 

我们考虑一个 cnt 数组，cnt[i] 表示 nums 中小于等于 i 的元素个数，如下图：

假设nums数组无重复的情况下，显然 cnt[i] ≤ nums[i]，也就是说 ≤ mid 的数量不会超过mid，例如上图中 ≤ 3 的数量最多就是 3 个，但是如果数组中有 1 个重复元素的情况下，就不一定能满足这个条件了：

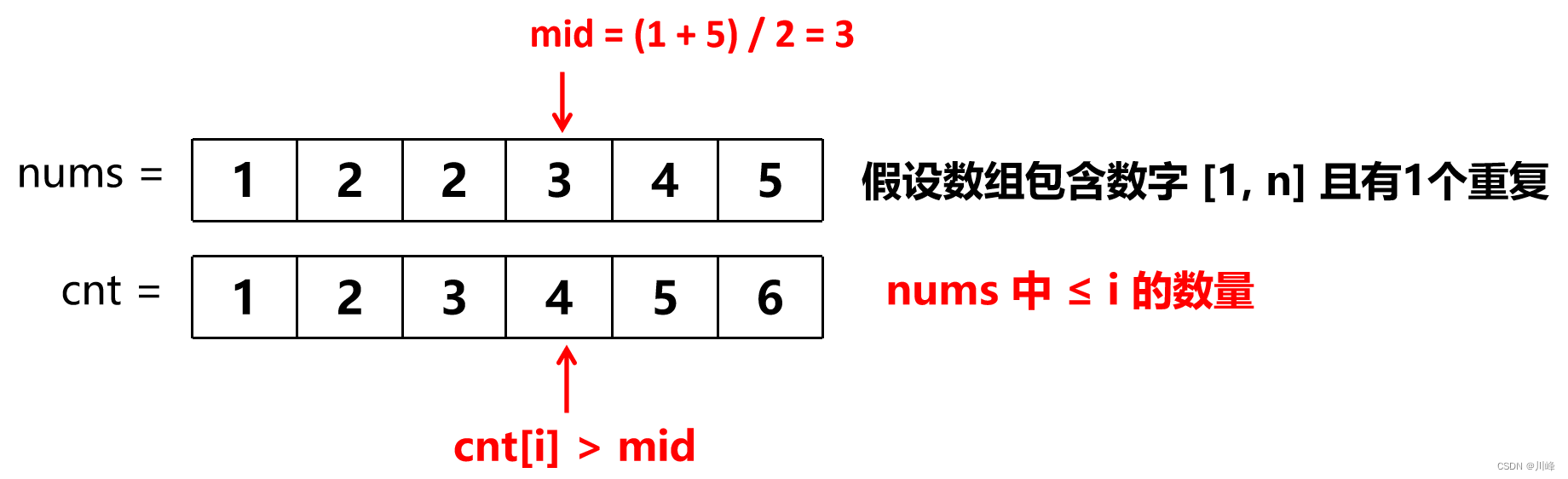
显然这是因为出现了重复数字导致的。 

虽然题目数组是无序的，但是cnt数组是逐步增大且具有单调性的，此题的二分思想就是利用cnt数组的特性来判断区间划分的。

• 3） 位运算 ， 统计 nums 中所有人的二进制在第 i 位上 1 的个数和记为 x ， 统计 [1-n] 中所有人的二进制在 第 i 位上 1 的 个数和记为  y ，如果 x > y , 则说明重复的数在第 i 位上二进制是 1 ，因此才会多出来  1  个数。我们只需将 32 位二进制位中 1 的个数多出的那一位的答案二进制位设置为  1  即可。

 

这个代码如果想更极致一点，可以先找出最大数 n 中最高位的 1 的位置，循环只需要处理到这一位即可，因为再高的就全是 0 了。参考代码：

27. 移除元素

 

• 1） 快慢指针 ，快慢指针从 0 开始，不断移动 快指针 ，把 快指针 遇到的 不等于 val 的值移动到 慢指针 的位置。

这个做法可以看到是利用原始数组本身来作为结果数组接收答案。 

解题思路： 

• 2） 对撞指针 ，当  L 指针 遇到要删除的元素  val  时，使用数组最后一个元素来覆盖这个元素，并且让 R-- 。
• 覆盖后的  L  处新数字有可能仍是要删除的元素，没有关系，在下一次 while 循环会接着判断处理，但是至少，我们从数组的最后删除了一个元素。
• 当  L 指针 遇到的元素不是  val  时，让 L++ 。
• while  循环条件是 L<=R ，因为每个数都要处理，最后返回 L  作为数组长度。

283. 移动零

• 1） 快慢指针 ，快慢指针从 0 开始，不断移动快指针，当 快指针 遇到的 非 0 数字 时， 就 交换快慢指针的元素值即可。
• 2)   快慢指针 ，快慢指针从 0 开始，不断移动快指针， 当 快指针 遇到的 非 0 数字 时， 直接覆盖到前面 slow 位置，然后 slow++ 。全部结束后，再把 slow 之后的位置都置为  0 。
• 3） 快慢指针 ，针对方法 2）优化： fast 遇到 非0 值覆盖到 slow 后，如果 fast 不等于 slow ， 就将 fast 直接原地置 0 ，然后再 slow++ 。

 

 

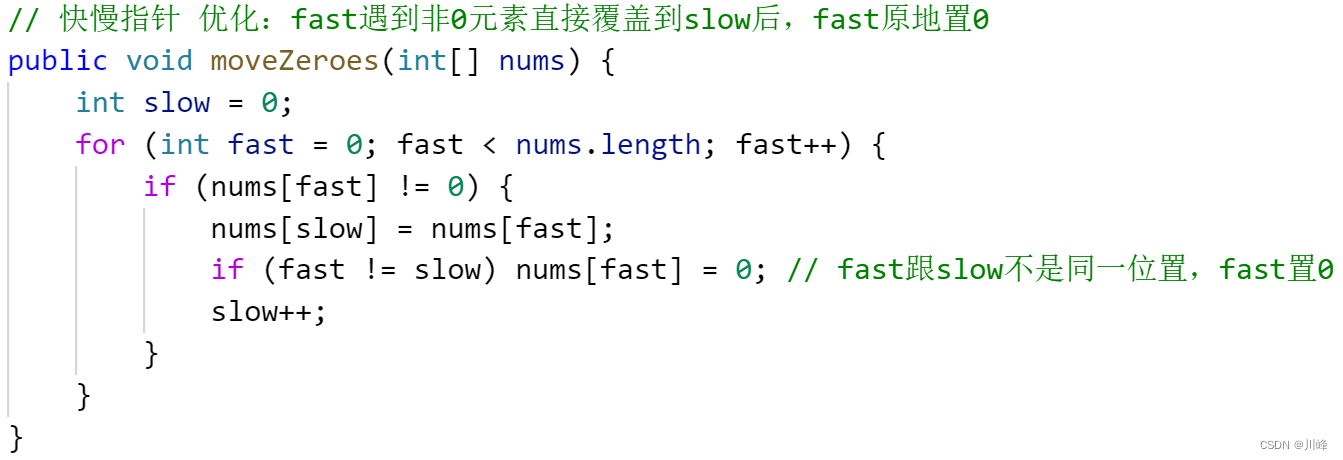
202. 快乐数

• 1） 哈希检测环 ，使用 HashSet 来判断重复，每次 while 循环判断只要  n != 1  并且也没包含在 set 中，就将  n  并加入 set 集合中，然后将 n 更新为 n 的各位数的平方和。
• 结束循环后返回 n 是否等于 1 即可（跳出循环只有两种情况要么 n 变成 1 要么 set 集合中出现了重复即有环）。
• 求  num  各位的平方和的技巧：每次  num % 10  取出个位数，然后计算平方累加到结果中， num / 10  去掉个位数，直到  num  变成  0  停止。 

虽然这道题在 LeetCode 上标记为 [简单] 难度，但是我觉得有一种情况是比较难观察出来的，那就是题目中说的除了最终得到 1 以外，最终也可以变成无限循环，这里的无限循环有可能是最终又遇到了重复的数字，也有可能是变得越来越大直到无穷大一直进行下去。也就是说可能会有两种情况，而在很多网课中讲解的这里仅仅只是默认按照重复数字套哈希表的解法。

下面看一下力扣官方的解释：

我们可以先举几个例子。我们从7开始。则下一个数字是49（因为72＝49），然后下一个数字是97（因为42＋92＝97）。我们可以不断重复该的过程，直到我们得到1。因为我们得到了1，我们知道7是一个快乐数，函数应该返回 true。

 

再举一个例子，让我们从 116  开始。通过反复通过平方和计算下一个数字，我们最终得到 58 ，再继续计算之后，我们又回到 58。由于我们回到了一个已经计算过的数字，可以知道有一个循环，因此不可能达到 1。所以对于 116，函数应该返回 false。 

 

根据我们的探索，我们猜测会有以下三种可能：

    1.最终会得到 1。

    2.最终会进入循环。

    3.值会越来越大，最后接近无穷大。

第三个情况比较难以检测和处理。我们怎么知道它会继续变大，而不是最终得到 1 呢？我们可以仔细想一想，每一位数的最大数字的下一位数是多少。

 

对于 3 位数的数字，它不可能大于 243。这意味着它要么被困在 243 以下的循环内，要么跌到 1。4 位或 4 位以上的数字在每一步都会丢失一位，直到降到 3 位为止。所以我们知道，最坏的情况下，算法可能会在 243 以下的所有数字上循环，然后回到它已经到过的一个循环或者回到 1。但它不会无限期地进行下去，所以我们排除第三种选择。

即使在代码中你不需要处理第三种情况，你仍然需要理解为什么它永远不会发生，这样你就可以证明为什么你不需要处理它。

• 2） 快慢指针检测环 ，慢指针和快指针初始值从 n 开始，在每次循环中，慢指针计算更新 1 次（ slow 更新为其各位平方和），而快指针计算更新 2 次 （ fast 更新为其各位平方和） ，直到出现 快指针 变为 1 ，或者 快指针 和 慢指针 相遇，就退出循环。
• 最后返回 快指针是否等于1 即可（如果是因为快慢指针相等退出循环的，说明存在环）。
• 注意： 快指针 会先遇到 1 。

注意上面代码中，最好使用 do-while 循环，不然可能上来就退出循环了，因为 slow 和 fast 都初始化为 n  ，当然由于前面已经分析了要么最终会变成1，要么会出现环（重复），所以你也可以直接写一个 while(true) 死循环来检测，在循环体里面写判断退出的条件。

快慢指针是用来检测有环问题的经典做法。

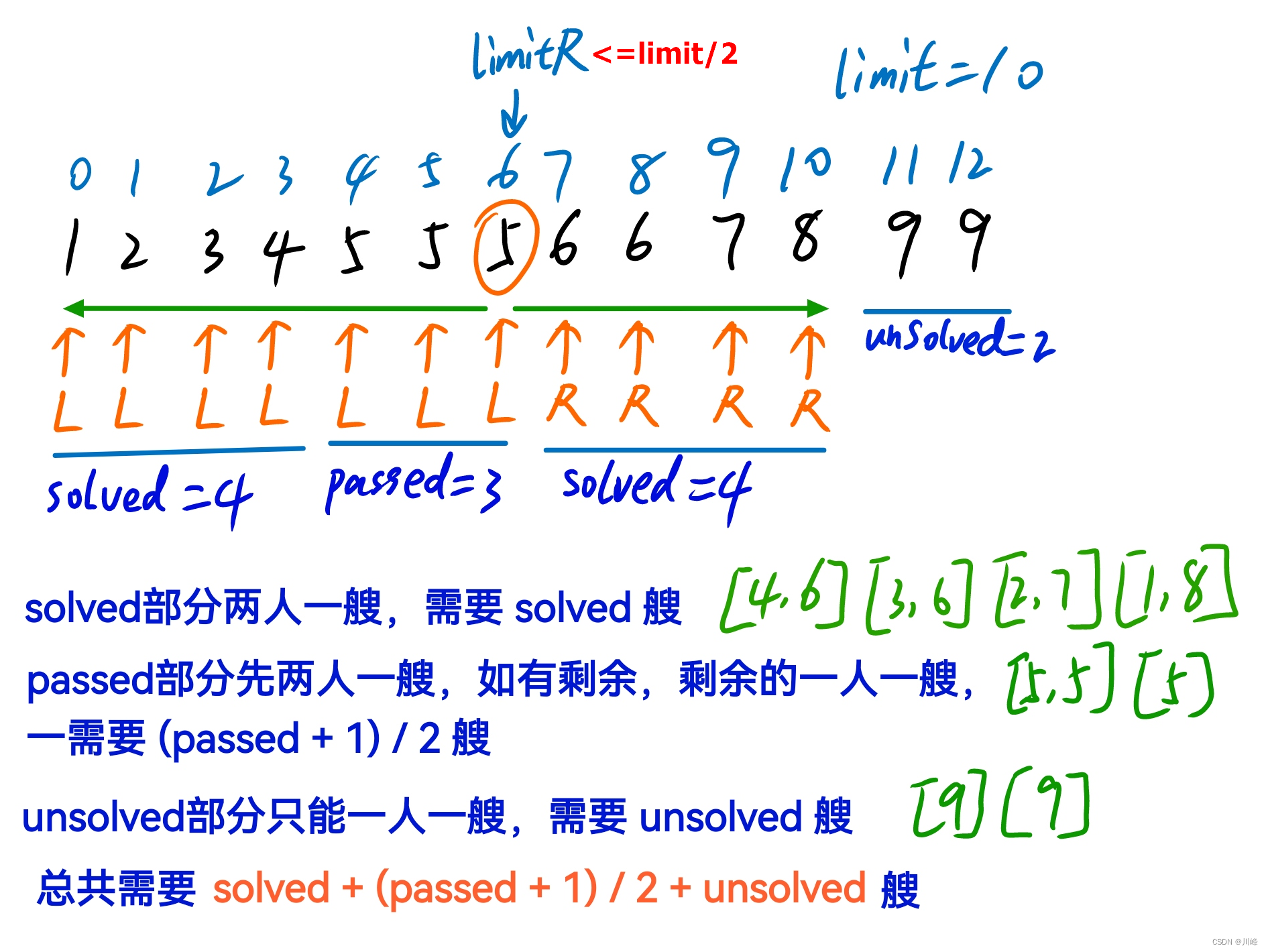
881. 救生艇

• 1） 排序 + 对撞指针 ，要求船数最少，那就应该尽可能多的坐满  2  人一船，剩下的人一人坐一船，因此 先排序 ，然后对撞指针从两头往中间挑选两个人的体重之和 <=limit 的坐一船，如果两个人的体重超过 limit ，只能较重的那个人自己坐一船。
• 循环结束时，如果  L == R ，则剩余的 1 人自己坐一船。 （注意退出循环也有可能是因为 L > R，所以最后返回时需要判断一下）

• 2） 排序 + 中心扩展， 也是需要 先排序 ，然后从 右往左 找到第一个 <= limit / 2 的位置，然后从该位置开始设双指针往 左右 同时 扩展 ， 寻找能够两个人坐一船的，剩下落单的人只能一人一船。
• 特判1：如果每一个人的体重都超过了限重的一半（ > limit / 2 ），那么只能一人坐一船，直接返回 people.length ，不用再继续了。因为此时任意两人体重之和都会超过 limit 。
• 特判2：如果最重的人体重 <= limit / 2 ，则此时任意两人组合体重和都不会超过 limit ，所以此时可直接安排 2 人坐一船，直接返回 (people.length + 1) / 2 。