来聊一聊独热码检测

国庆假期不小心扭伤了脚踝，在家没事看到一篇文章挺有意思，于是写出来分享给大家。

这是一道数字电路面试题，也是很多面试官很喜欢考察面试者的一道题目，题干很简单：给定一个4bit的信号A，设计逻辑来判断A是不是独热码，设输出为Y，如果A是独热码，则输出1，如果不是，则输出0；

首先我们来看什么是独热码（one-hot），独热码是一种二进制编码方式，它的特点是，用来编码的这个数的N位bit中，有且只有一位是1，其余位全部都是0，因为只有1位是1，所以叫做one-hot（对应的，还有一种编码方式是只有1位是0，其余位都是1，叫做one-cold）

下面的表格是独热码来表示0-7这8个数。

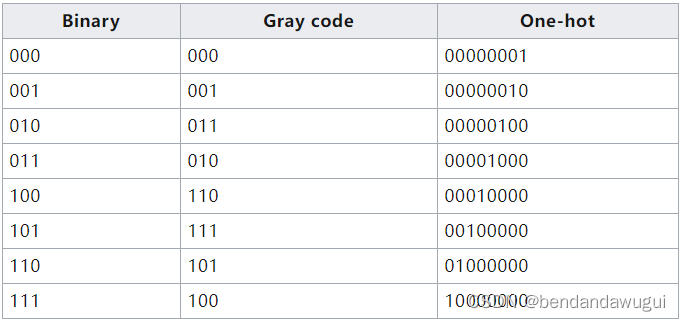
其实one-hot编码在电路设计中非常常见，举个简单的例子，给定一个SRAM的地址，要读出SRAM中的一行，SRAM内部就是利用address的某几位来转换为one-hot的select从而选中对应的word line和bit line，还有一些场合，利用one-hot来编码状态机，好处就是一个flop就表示一个状态，用来判断状态机在哪一个状态的时候就只需要看第几个flop为1即可，而不需要像binary编码那样是所有flop在一起参与比较，这样可以省下来一点点逻辑比较电路的延时，代价显而易见，用one-hot编码状态机需要的寄存器比binary编码要多，这就是一个典型的利用面积换性能的trade off；

回到这个问题本身，其实直接回答上面这个问题难度不大，相信所有学过数字逻辑的同学都能都立刻想到解决办法--利用真值表和卡诺图，这也是面试官要考察你的第一层，对于学校的课程基础支持掌握的是不是扎实。

真值表略过，直接上卡诺图：

很明显，在这个例子中，卡诺图并不能帮我们简化逻辑（为什么？）最后的表达式其实都可以直接想到。

Y = (A[0] & (!A[1]) & (!A[2]) & (!A[3])) 
   |((!A[0]) & A[1] & (!A[2]) & (!A[3]))
   |((!A[0]) & (!A[1]) & A[2] & (!A[3]))
   |((!A[0]) & (!A[1]) & (!A[2]) & A[3]);

【卡诺图中的1/0是怎么来的？其实是根据真值表来的，为1的项表示真值表可能存在的值，以1000为例，这一项就是这个one-hot可能存在的一个值，因此在卡诺图中该项为1】

这个时候面试官可能会问你，需要多少个逻辑门，关于上面的表达式，假设我们有四输入的与门和四输入的或门，而且假设输入可以取反，那么我们就需要4个与门，1个或门，如下图所示：

回答到这里，面试官可以认为你在数字电路的课没有完全睡觉，至少最基本的只是你是掌握的，能够回答出这个答案不一定会给你offer，但是回答不出来那肯定是对不起谢谢了。

那么接下来面试官会进一步问，如果输入变成了16bit，甚至32bit或者更多呢，你要怎么设计电路？如果用verilog来表示你的电路呢？

当然你可以继续使用卡诺图和真值表，直接写表达式，16个最小项，再把他们或起来，可是你知道这不是面试官想要的答案，因为面试官想要你设计的，是一个参数化的表达，参数化的设计是数字逻辑设计中很重要的一个点，它体现了你的设计是不是可以复用，而且能够匹配各种应用需求，以这个为例，面试官想要你设计的其实是下面这个function。

parameter WIDTH = 16;
function is_one_hot（input[WIDTH-1:0] signal）
// code your rtl
endfunction

那么让我们想一想该如何解决这个问题，其实有个很简单的思路，就是从独热码的定义出发：只有一位是1，其余位都是0，那么不管我们输入信号有多少位，有一个性质是不变的--把这些位加起来，最后的结果肯定是1，那么我们就可以利用一个for循环，把每一位相加，最后把最终的和1比较一下，如果是1，那就是独热码，如果不是1，那就是其他的数，非常的直观。

当然，如果你告诉面试官这个思路，面试官会很乐于让你写以下RTL code，code不长，只要你能写出来，没有语法错误，那你在面试官心里又加了一分，下面是一个上述思路的RTL参考code。

function automatic logic is_one_hot(input [WIDTH-1:0] signal)
parameter SUM_WIDTH = $clog2(WIDTH)+1;
logic [SUM_WIDTH-1:0] sum;
sum = 'd0;
for (int i =0; i< WIDTH; i++)
  sum = sum + sig[i];
  is_one_hot = (sum ==1);
endfunction

如果你能写出上面的代码，特别是能注意到automatic $clog2等，说明你对systemverilog掌握的不错，是写过几行代码的人，如果你是一个应届生，能够写出这样的code，并且能够回答出面试官针对这几行code的问题，面试官已经对你很感兴趣了，这里面有几个小点需要大家注意，SUM_WIDTH要用$clog2之后再加1，为什么要这样大家自己思考一下。

那么面试官下来就会问你，这段code综合出来的电路是什么样子的呢？这里面试官想考察你对for loop在RTL中实际理解，对于许多RTL的初学者，通常搞不清楚for loop的作用，错误的把程序设计中的for循环的想法滥用在RTL设计中，这里我们一直在强调，RTL的每一行代码都是在面熟电路，大家一定要做到心中有电路，手下才有code。

上面的电路以WIDTH=4为例，综合处的电路（优化前）其实是：

很明显，这样的电路可以达到设计的目的，但是并不是最优的，大家可以计算以下每个2bit full adder需要多少门，comarator需要多少门，再和之前利用卡诺图方法得出的最简电路比较一下。

那么有什么办法可以优化呢？当然如果你继续对上面的思路进行优化，比如第一级，第二级其实不需要一个2bit的adder，而是可以将a[0]，a[1]，送到一个half adder里面，这样就可以替换掉前面两个2bit adder，还有half adder本质其实就是一个XOR gate等等，这些都是面试官很乐意和你探讨的，你探讨的越细，在面试官心里的加分就越多，其实在面试过程中你是不是给出最优解并不关键，重要的是给面试官展现出来你的思考过程，展现出你利用现在有的只是去一点点解决未知问题的能力，一般来说，如果这道题目你经过这么一个思考过程，包括写代码画电路和面试官讨论，你在这个问题上的表现已经在面试官心里有谱了。

那么这个问题再上一个层次要怎么回答呢？其实思路来自一个稍微冷门但其实又非常常用的知识点：对一个binary number进行奇偶校验。

举例来说，对于一个4位的二进制数，我们对这4位奇偶校验，利用XOR门依次进行每一位运算，最后的结果，如果4位binary有奇数个1，那么4位XOR之后的结果就是1，如果有偶数个1那么结果就是0，看到了吗，我们要找的独热码其实就是奇数个1的特殊情况，即只有一位是1，所以更加巧妙的方法就是来自于这个按位XOR。

我们再来看几个例子，看能不能找出独热码按位XOR的特点，还是以4位为例，我们定义如下运算，把A相应按位XOR的结果记为P，其中P[0] = A[0] ，P[i] = A[i] ^ P[i-1] 。

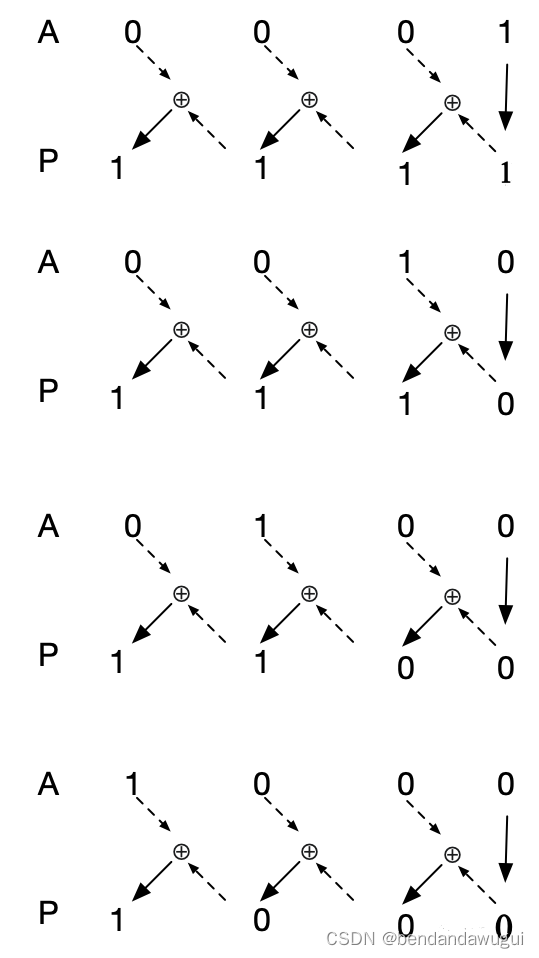
我们可以看到一个规律，即对于独热码，我们得到的P会是这样一个数：如果独热码A的第i位为1，那么P的第i-1到第0位都是0，而第i位和更高位都是1，注意这个规律只对独热码适用，大家可以试验以下其他任何数，只要多于1位是1，那么就不会出现高位连续的都是1，高位必然会出现0；

那么我们就可以继续观察，如果我们将A按位取反，然后再和P按位OR起来会得到什么？A既然是独热码，那么除了为1的那一位（假设是第i位），取反之后都会变成1，只有第i位会是0，而P的第i位是1，那么最后按位OR的结果是什么？——全部每一位都是1。

那么如果A不是独热码，而是有两个1或者更多1，假设第i位和第k位是1（k是i之后第一个1），我们进行上面的操作会得到什么？P[k]会得到0，A反和P按位OR之后第k位也是0。

至此，我们距离最终答案只有一步之遥，A反和P按位OR之后的结果我们再对每一位进行按位AND，得到的结果如果是0，那么一定不是独热码。

为什么是一步之遥呢？我们这里漏掉了一个特殊情况，即A为全0，当A为全0的时候，P也是全0，但是A取反之后是全1，所以A反和P按位OR之后也会得到全1，幸好，特殊情况就只有一种，我们只需要对A进行一下全0的判断就可以了。

function automatic logic is_one_hot(input [WIDTH-1:0] signal)
  logic [WIDTH-1:0] parity;
  parity[0] = signal[0];
  for (int i=1; i< WIDTH ; i++)
     parity[i] = signal[i] ^ parity[i-1];
  is_one_hot = parity[i-1] & (&(parity | ~sig));
endfunction

至此，这个问题就讲的差不多了，说实话能够回答出最后一种解法的人寥寥无几，作为一道面试题，这道题的区分度其实并不怎么样，面试官更看重面试者是否能够顺利的利用前面基本思路来给出一个可以work的解法。

转载：面试题分析--独热码检测