角谱计算时的fftshift及其原理

news2024/10/7 14:24:58

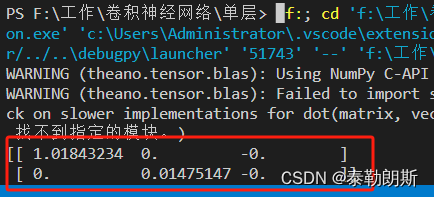
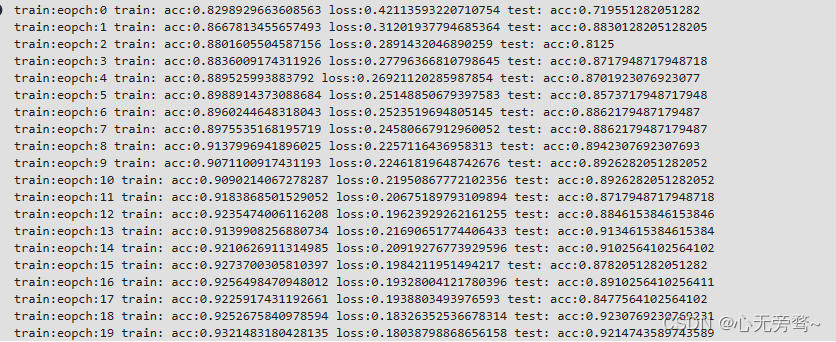
做一个fft运算，第一个事先用fftshift对待变换的E0进行操作，第二个没有用fftshift，第三个没有用fftshift但是进行了相位手动修正：

%%用fft进行角谱传输计算
%对比fft运算与傅里叶变换（黎曼和）的区别以及修正
clear
clc
close all

scale = 1.5e-4;
N = 50;
d0 = 20e-6;%sampling interval
wave_len=632.8e-9;%wavelength in nm 
k0=2*pi/wave_len;% vacuum wave number
fs=1/d0;%sample frequency
z=k0*scale^2;

x=d0*(-0.5*N:1:0.5*N-1); 
E0=abs(x)<scale;
I0=abs(E0).^2;

%初始面光强
figure(1)
plot(x,I0);
drawnow

%初始面相位
figure(2)
plot( x,mod(angle(E0),2*pi));
 
%傅里叶变化
figure(3)
ufft10=fftshift(fft(fftshift(E0)));%fftshift就是把频率平移，自己查资料，百度也行。如果不平移，那得知道每个地方对应的真实频率。
ufft10=ufft10';

subplot(1,3,1)
plot(mod(angle(ufft10),2*pi));

p=0:N-1;
ufft11=fftshift(fft(E0));%fftshift就是把频率平移，自己查资料，百度也行。如果不平移，那得知道每个地方对应的真实频率。
ufft11=ufft11';
subplot(1,3,2)
plot( mod(angle(ufft11),2*pi));

ufft12=fftshift(exp(1i*pi*p).*fft(E0));
ufft12=ufft12';
subplot(1,3,3)
plot( mod(angle(ufft12),2*pi));
%由于计算误差，可能会出现0和2pi的区别，画图可能会看起来相位不一样，所以可以直接看数据。