A*算法和Dijkstra

news2025/2/1 9:49:45

A*算法

个人理解F=G+H，F是总距离，G是已经走过的距离，F是暂未走过的距离，通过不断探索领进路径直至所有路径都到达终点，然后反向去确定最短路！
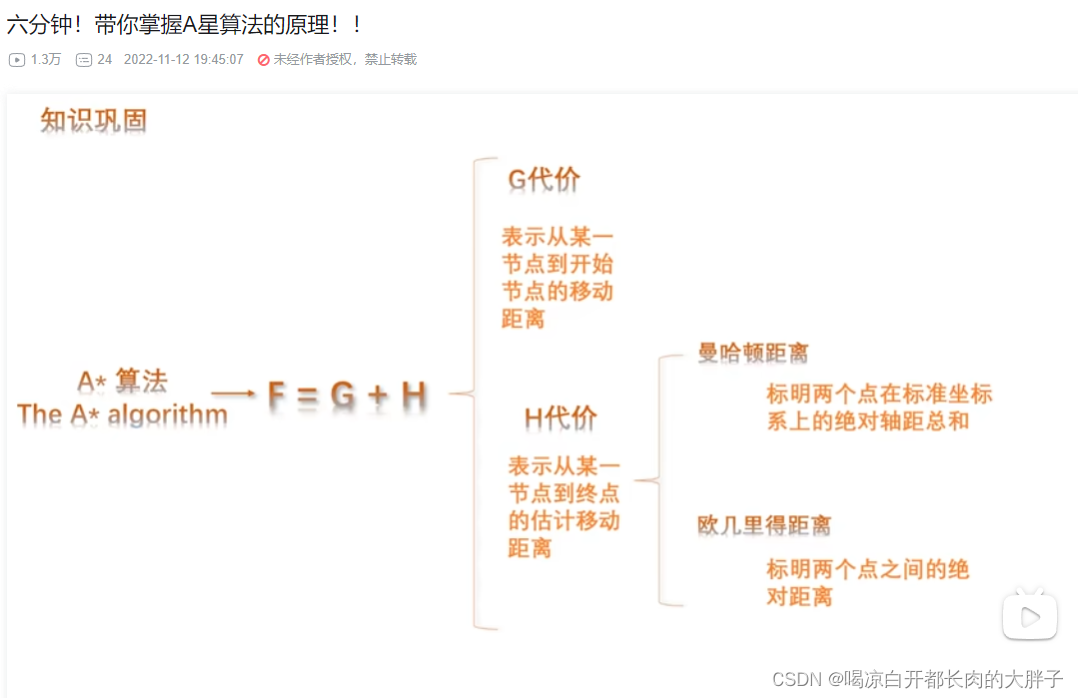
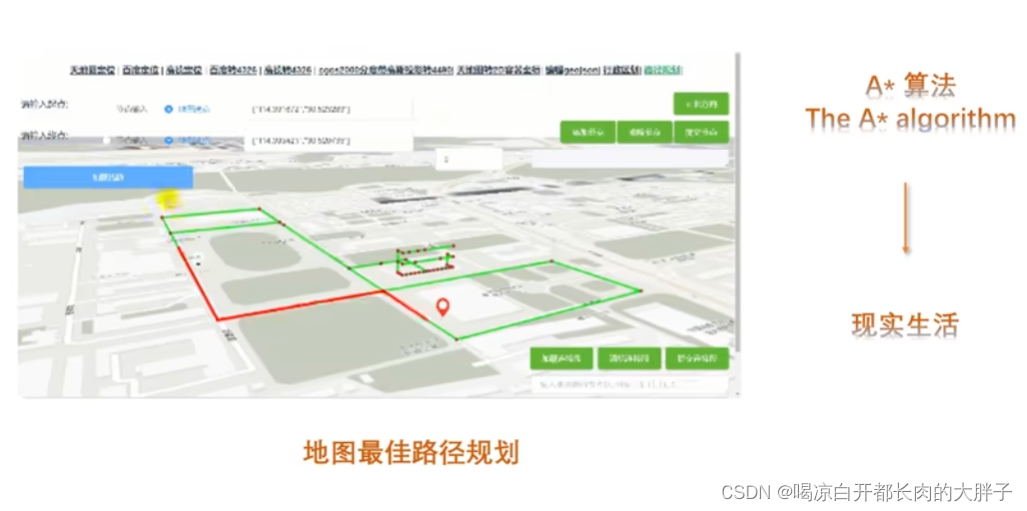
在这里插入图片描述

A*算法是静态路网中寻找最短路的最有效算法！

在这里插入图片描述

G是确定的，H是不确定的

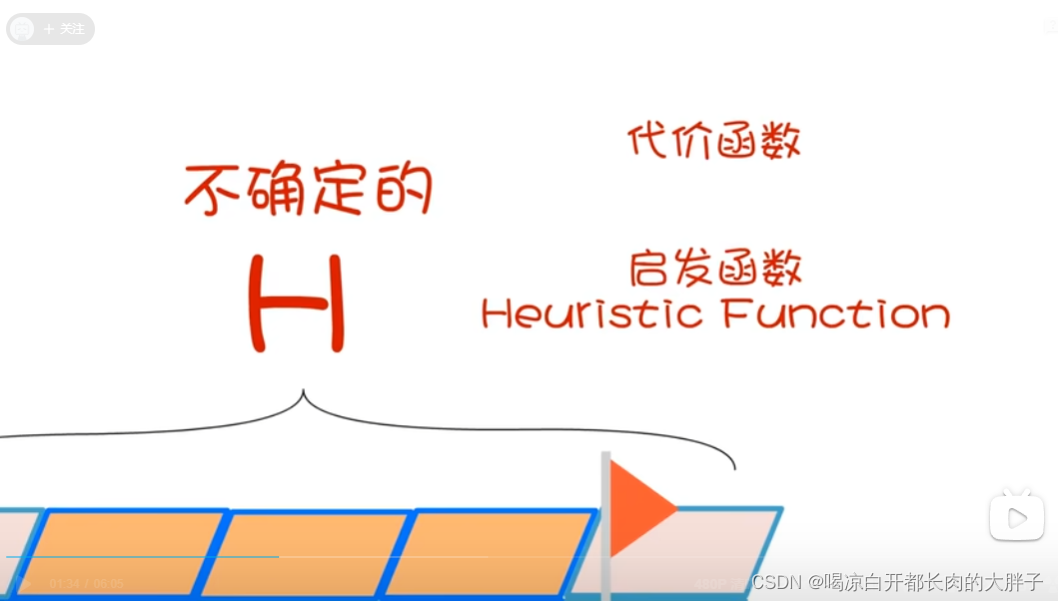
在这里插入图片描述

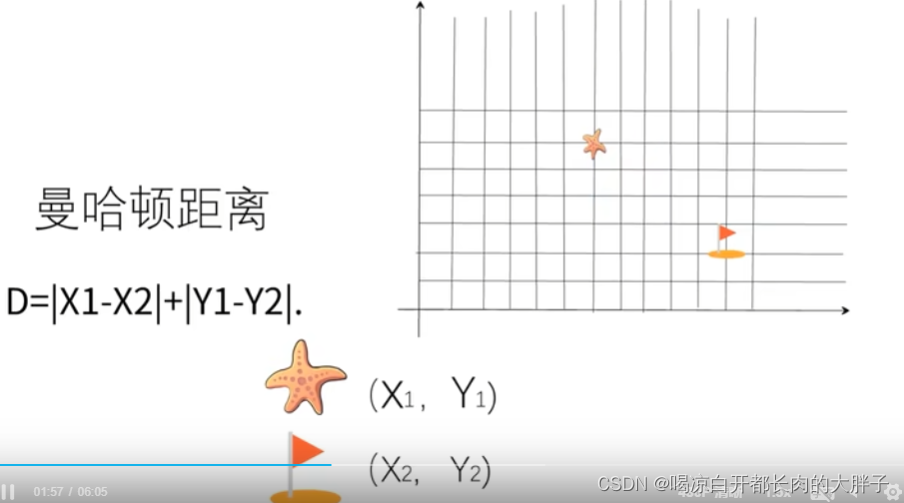
H取决去启发式函数，常用的启发式函数有欧几里得距离函数和曼哈顿距离函数

**在这里插入图片描述
**

Dijkstra算法

Dijkstra
Dijkstra,个人理解相当于在一个已知权边图的问题中，添加一个列表记录路径和总行驶距离，在距离中每次都按照最小的进行选择，结合图中距离选择下一个节点，进行记录，直至所有节点都选择完成，从而实现最短路的选择。
Dijkstra算法讲解视频

比较

Dijkstra算法和A算法都是最短路径问题的常用算法，下面就对这两种算法的特点进行一下比较：
Dijkstra算法计算源点到其他所有点的最短路径长度，A关注点到点的最短路径(包括具体路径)。
Dijkstra算法建立在较为抽象的图论层面，A算法可以更轻松地用在诸如游戏地图寻路中。
Dijkstra算法的实质是广度优先搜索，是一种发散式的搜索，所以空间复杂度和时间复杂度都比较高。对路径上的当前点，A算法不但记录其到源点的代价，还计算当前点到目标点的期望代价，是一种启发式算法，也可以认为是一种深度优先的算法。
由第一点，当目标点很多时，A*算法会带入大量重复数据和复杂的估价函数，所以如果不要求获得具体路径而只比较路径长度时，Dijkstra算法会成为更好的选择。
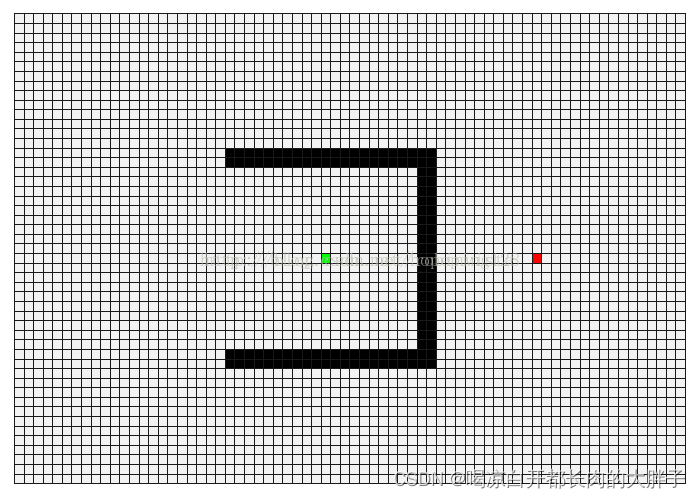
在这里插入图片描述
动图查看原文
原文链接：https://blog.csdn.net/hopeping128/article/details/78960326