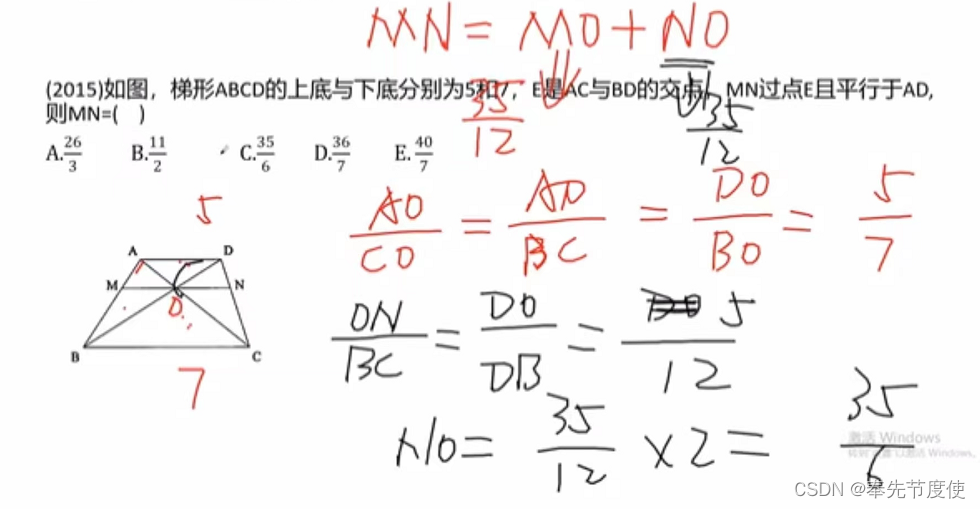2024级199管理类联考之数学基础(下篇)
平面几何(平均2题)
三角形(性质、特殊三角形、全等与相似)
- 性质
- 由不在同一直线的三条线段首尾依次连接所组成的图形
- 三条边、三个内角、三个定点
- 三角形内角和为180度,外角和为360度,多边形的外角和为360度,n多边形的内角和为(n-2)*180度
- 一个外角等于不相邻的两个内角之和
- 任意两边之和大于第三边,任意两边之差小于第三边,即大角对大边,等角对等边
- 三角形的两边中点的连线平行于第三边,且等于第三边边长的一半
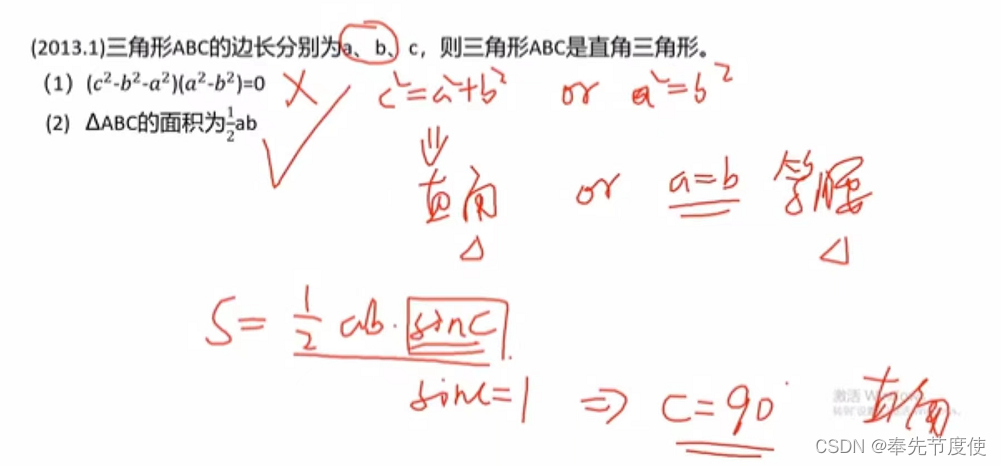
- 三角形面积S=1/2ah=1/2absinC
- 当已知条件仅说明三条边的长度,那就需要使用海伦公式S=根号下p(p-a)(p-b)(p-c),其中p=1/2(a+b+c)
- 三角形四心
- 内心:三角形内角平分线的交点(即三角形内切圆的圆心,到三角形三边的距离相等)
- 外心:三条边的垂直平分线的交点(三角形外接圆的圆心,到三个顶点距离相等)
- 重心:三条中线的交点
- 垂心:三条高线的交点
- 等边三角形四心合一,等腰三角形底边四线合一
- 三角形面积考点
- 两个三角形
- 同底等高,则面积相等
- 同底不等高,面积比等于高之比
- 等高不同底,面积比等于底之比
- 蝶形定理(针对梯形)
- 梯形ABCD中,下底与上底之比为k,即CD:AB=k:1
- 若蝴蝶头部Sabe=S,则蝴蝶腰部Sade=Sbec=kS,蝴蝶尾部Sdec=K^2S
- 即蝴蝶腰部*蝴蝶腰部=蝴蝶头部*蝴蝶尾部(即三部分面积成等比数列)
- 三角形分类
- 直角三角形
- 勾股定理(等价于外国称为毕达哥拉斯):a^2+b^2=c^2(a^2+b^2>c^2表示锐角三角形,反之为钝角三角形)
- 射影定理
- 斜边上的高是两直角边在斜边上射影的比例中项,即高^2=射影1*射影2
- 每一条直角边是这条直角边在斜边上的射影和斜边的比例中项(直角边^2=斜边*射影)
- 等腰直角三角形
- 边长关系比为1:1:根号下2
- 面积公式S=1/2a^2=1/4c^2,a为直角边,c为斜边
- 锐角为30度的直角三角形30度对边的边长为斜边一半,三边关系为1:根号下3:2
- 等腰三角形
- 四线合一: 底边高、中线、垂直平分线、顶角角平分线
- 120度的等腰三角形,三边比例为1:1:根号下3,如果腰长为a,则面积S=根号下3/4 *a^2
- 等边三角形
- 三角形全等、相似
- 全等:两个全等三角形的对应边相等、对应角相等
- 判定全等的充分条件
- 两个三角形有两条边及其夹角对应相等(SAS)
- 两个三角形有2个角及其夹边对应相等(ASA)
- 两个三角形3条边对应相等(SSS)
- 相似
- 性质:两个相似三角形面积比=相似比平方
- 判定充分条件
- 两个三角形有一个内角对应相等,其两条夹边对应成比例
- 两个三角形有2个内角对应相等
- 两个三角形的3条边对应成比例

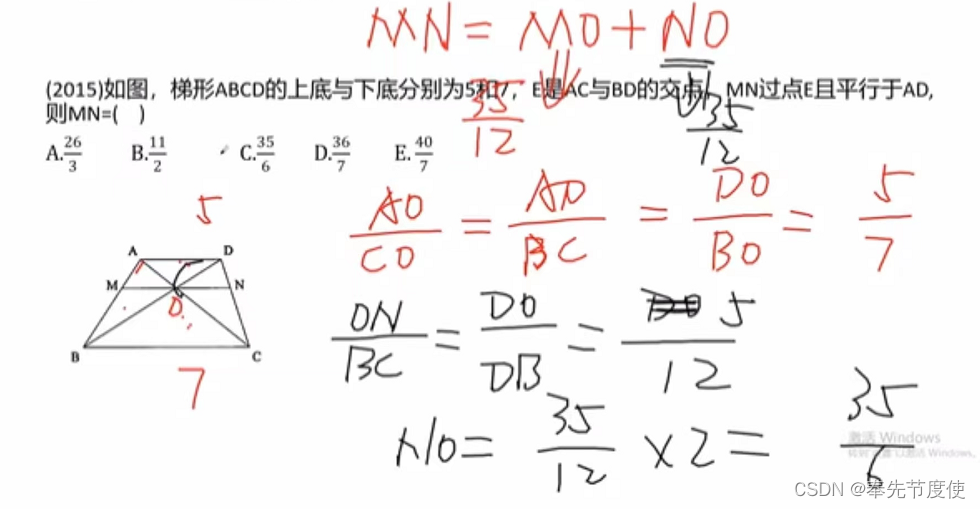


四边形(平行四边形、矩形、正方形、菱形、梯形)
- 平行四边形性质
- 平行四边形对边相等,对角相等,对角线互相平分
- 一对对边平行且相等的四边形
- S平行四边形=ah(底*高),周长C=2(a+b)
- 菱形性质
- 有一组邻边相等的平行四边形
- 四边相等的四边形一定是四边相等的平行四边形,即菱形
- 菱形的对角线互相垂直且平分顶角
- S菱形=1/2L1*L2(L1、L2为两对角线的长)
- 矩形性质
- 正方形性质
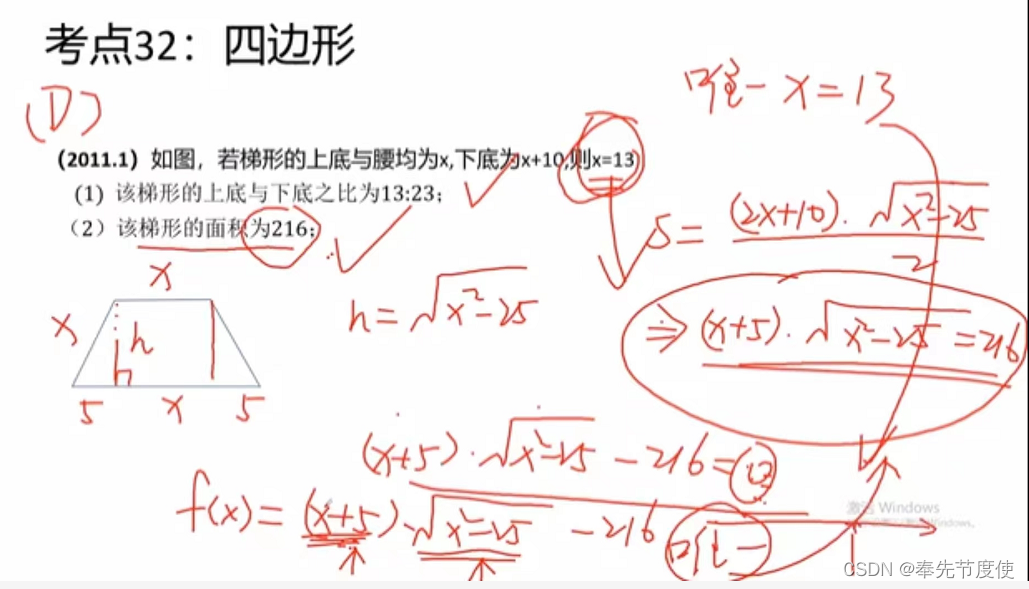
- 梯形性质
- 一对对边平行
- 梯形两腰中点连线称为梯形的中位线且=1/2(上底+下底)
- S梯形=1/2(上底+下底)*高
- 等腰梯形性质
- 两条腰相等或者两个底角相等
- 两条对角线相等
- 若两对角线相互垂直,则高与中位线长度相等
圆
- 定义/性质
- 平面上与定点o距离等于定长r的动点轨迹称为圆,点o为圆心,r为半径
- S圆=πr^2,C圆=2πr
- 连接圆上任意两点的线段叫做弦,经过圆心的弦叫做直径
- 圆上任意两点间的部分叫做圆弧,大于半圆叫做优弧,小于半圆叫做劣弧
- 定点在圆上的角,它的两边分别与圆还有另外一个交点称为圆周角
- 一条弧所对的圆周角是它所对圆心角的一半
- 直径所对的圆周角为90度,90度圆周角所对的弦是直径
- 圆内两条圆弧相等,圆弧所对应的两组圆心角相等,两组圆周角也相等,即等弧对等角
- 圆的切线与圆的半径在切点出垂直
- 从圆外一点作圆的切线,两条切线相等
- 垂直定理
扇形
- 角的弧度
- 扇形面积=n/360度*πr^2(n为扇形对应的圆心角角度,r为扇形半径)
- 弓形面积=S扇形-S三角形



立体几何(平均1题)
长方体
- 性质
- 6个面,12条棱,8个角
- V体积=abc,S面积=2(ab+ac+bc),体对角线d=根号下a^2+b^2+c^2
正方体
- 性质
- S面积=棱长*棱长*6=6a^2,V体积=a^3
- 体对角线=根号下3*a同时也是正方体中最长的线段
圆柱体
- 性质
- V体积=底面积*高=πr^2*h
- S侧面积=2πrh,S全面积=侧面积+底面积=2πrh+2πr^2
- L对角线=根号下(h^2+(2r)^2)
球体
- 性质
- R为球上一点到球心的距离,直径d=2R
- V体积=4/3πR^3
- S表面积=4πR^2

解析几何(平均2题)
平面直角坐标系

平面直线
- 直线的倾斜角与斜率
- 倾斜角:直线与x轴正方向的夹角a,0<=a<=180度
- 斜率k:反映直线的倾斜程度,记为k=tana=(y2-y1)/(x2-x1)(a!=90度)
- 常见的两者对应关系
- tan0=0;tan180=0;tan45=1;tan135=-1;tan60=根号下3;tan120=-根号下3
- 直线方程常见形式
- 直线的点斜式:y-y0=k(x-x0),表示斜率为k且过点(x0,y0)的一条直线
- 直线的斜截式:y=kx+b表示斜率为k且与y轴相交于点(0,b)的直线,其中称b为直线的纵截距
- 直线一般方程:ax+by+c=0(a与b不全为0)
- 若a=0,方程为水平直线y= -c/b
- 若b=0,方程为竖直直线x= -c/a
- 若c=0,直线过原点(0,0)
- 若b!=0,则方程可写为y=-a/bx-c/b,直线斜率k=-a/b,纵截距y=-c/b,横截距x=-c/a
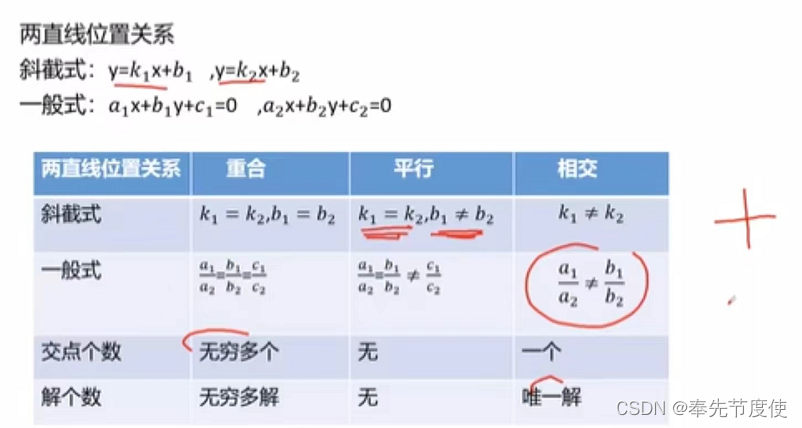
- 两直线位置关系



圆(直线与圆、圆与圆关系)
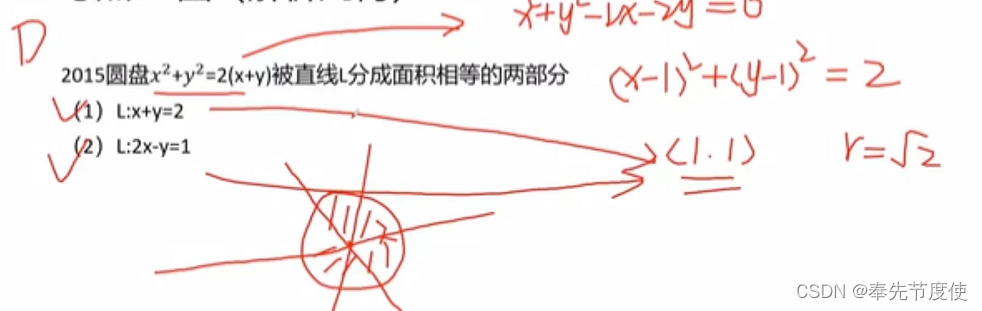
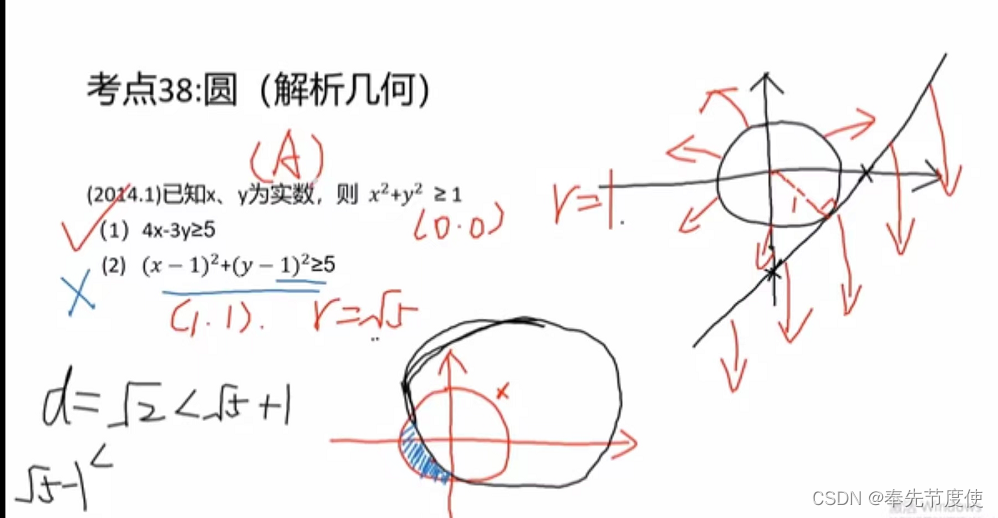
- 圆的方程
- 标准方程:以O(a,b)为圆心,r为半径的圆的方程为(x-a)^2+(y-b)^2=r^2
- 一般方程:x^2+y^2+Dx+Ey+F=0《=》(x+D/2)^2+(y+E/2)^2=D^2+E^2-4F/4;
- 可以得到圆心坐标O(-D/2,-E/2),半径r=根号下(D^2+E^2-4F)/2



排列组合(平均1题)
加法与乘法原理
- 分类计数原理(加法原理):完成一件事,有n类办法,每类有多种方法,那么完成这件事的方法=每一类拥有的方法进行相加求和
- 分步计数原理(乘法原理):完成一件事,需要分成n个步骤,每步有多种方法,那么完成这件事的方法=每一步拥有的方法进行相乘求积
- 核心区别:能独立直接完成的属于分类计数(加法原理),不能直接完成需要分步完成的属于分步计数(乘法原理)
组合与组合数

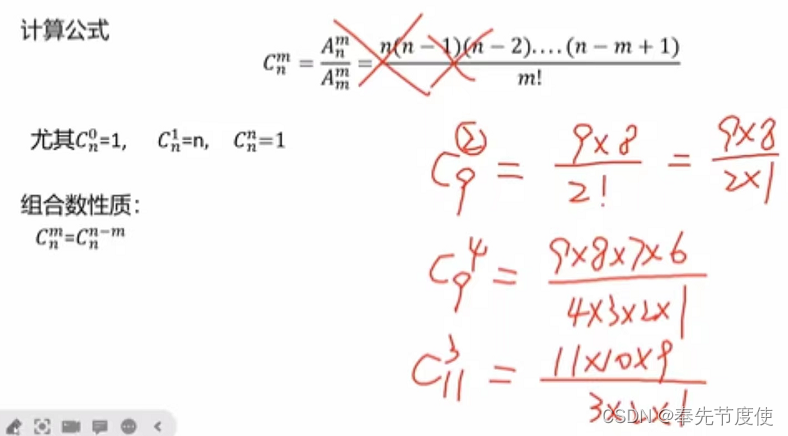
排列与排列数



排列组合步骤
-
先取后排:先选取出元素,然后再进行排列元素,不要边取边排(容易做错)
-
依次进行:按照一定的先后顺序排列
-
事情完成:整个事情必须完成
排列组合秒杀思路
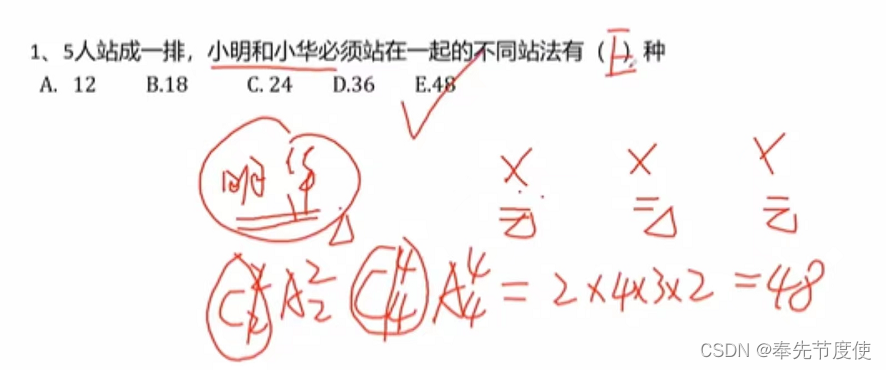
- 相邻问题/打包捆绑法
- 该方法主要解决若干个元素相邻问题
- 考题常见自然语言描述:紧挨着、相邻、一起...
- 解题思路:优先解决特殊要求的元素,并捆绑打包成一个整体
- 不相邻方法/插空法
- 该方法主要解决若干个元素不相邻问题
- 考题常见自然语言描述:不挨着、不相邻、不能连续...
- 解题思路:优先安排无任何要求的元素,再把特殊元素放入空位

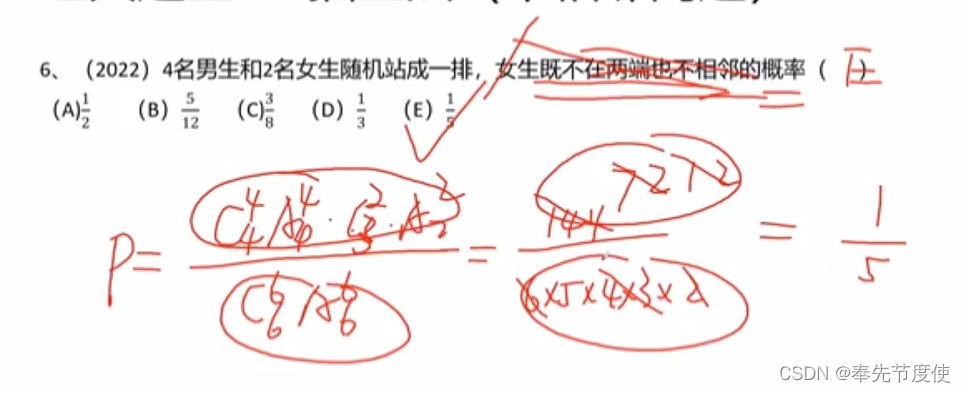
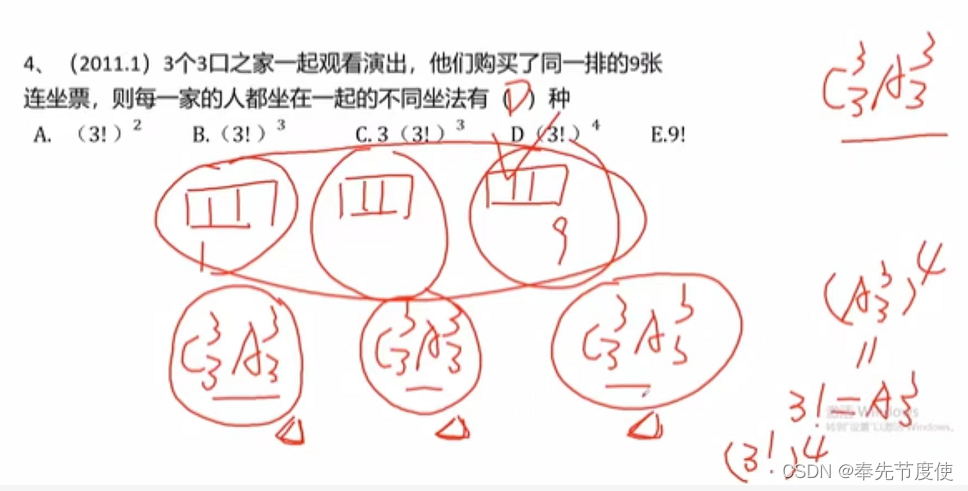
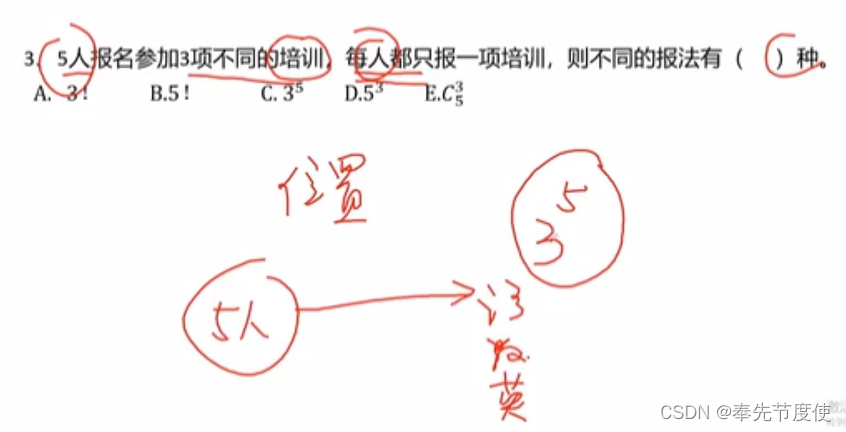
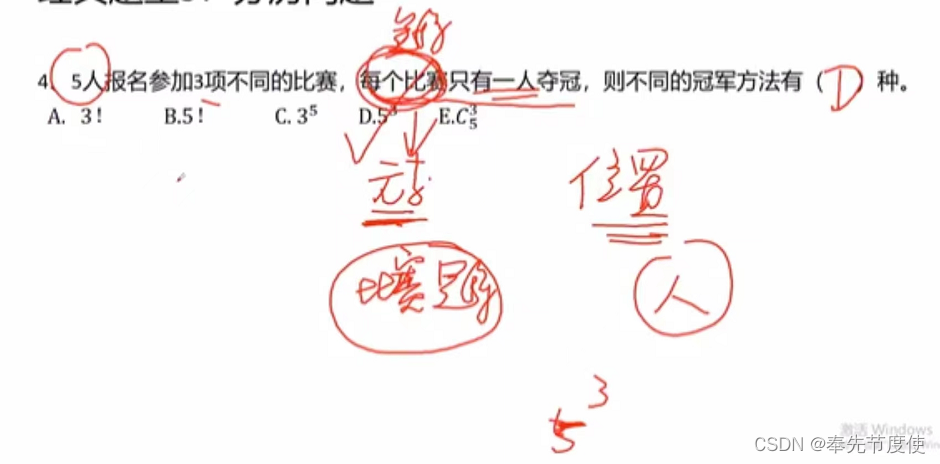
- 分房法(高频考点)
- 不同元素分配给不同的对象,对于分配对象分配的元素个数无限制
- 考题常见自然语言描述
- n个人去往m个不同的房间
- 个球放入m个不同的盒子
- n封信放入m个不同的信箱
- 解题思路:n个不同元素(指数位置)分配给m个位置(底数位置)对象,有m^n种方法
- 技巧:题目中只要出现"每”字,则紧跟着它的就是元素,即位于指数位置
- 隔板法
- 相同元素分配给不同的对象,每个对象至少分到1个
- 考题常见自然语言描述
- n颗相同糖果分给m个小朋友,每人至少一个
- n个相同的球分给m个不同的盒子,每个盒子至少分一个小球
- n张相同的奖状分给m个不同的班级,每个班级至少一张奖状
- 解题思路:n个相同元素分配给m个不同对象,有C(m-1)(n-1)种方法


- 对号不对号
- 不对号问题
- 2个不对号,有1种方法
- 3个不对号,有2种方法
- 4个不对号,有9种方法
- 5个不对号,有44种方法


- 特殊元素问题
- 一个元素具备两个属性或多个属性,选取时要注意全能元素的归属
- 考题常见自然语言描述
- 某人既会英语又会法语
- 某人既会唱歌又会跳舞
- 解题思路:对全能元素进行分类讨论,含与不含全能元素的分类


- 局部元素定序法
- 当把n个元素进行排序的时候,其中若有m个元素是按照一定顺序已经定序
- 考题常见自然语言描述
- 甲乙丙从高到低
- 甲乙丙3人按照年龄大小
- 解题思路:此时就要把其中m个元素的顺序去掉,有多少就除以多少,定序公式=Ann/Amm


- 局部元素相同法
- 当对n个元素进行排序时,出现m个元素是完全相同的情况
- 考题常见自然语言描述
- 几个字母排序时出现3个A
- 挂旗时出现相同颜色的旗帜,如3面红旗
- 解题思路:根据所有元素数量的阶乘,除以相同元素数量的阶乘,有多少除以多少,定序公式=Ann/Amm


- 分堆与分配问题(高频考点)
- 若分堆出现相同数量的堆数,则要除以相同堆数的阶乘,以消除排序,若题目要求对元素进行分配,则一定先分堆再分配





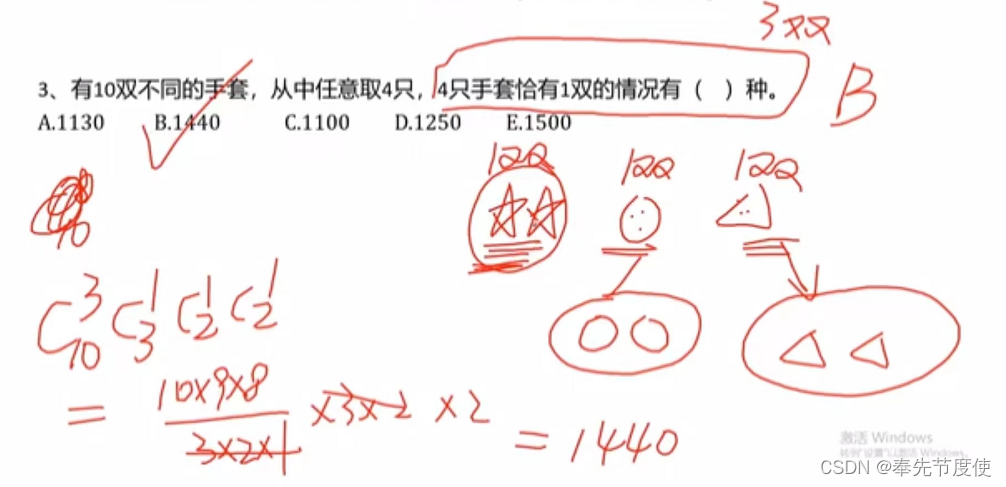
- 成双问题/配对问题
- 主要是以手套、袜子或鞋子等成双的物品作为对象,核心在于选取物品是否成双
- 成双问题:直接选取成双即可
- 不成双问题:先取双,再在双中取单只



概率(平均1题)
随机事件相关概念
- 随机试验
- 实验可在相同的条件下重复进行
- 可能结果不止一个,且所有可能结果已知
- 每次实验出现的哪个结果是未知的
- 如:掷骰子,观察出现的点数
- 不可能事件概率是0,必然事件概率是1,随机事件概率(0,1)
- 事件A与事件B同时发生的事件为A与B的积事件即AB
- 事件A与事件B至少有一个发生的事件为A与B的和事件即A+B
概率定义与分类
- 事件A的概率是指随机事件A发生可能性大小的度量值记作P(A)
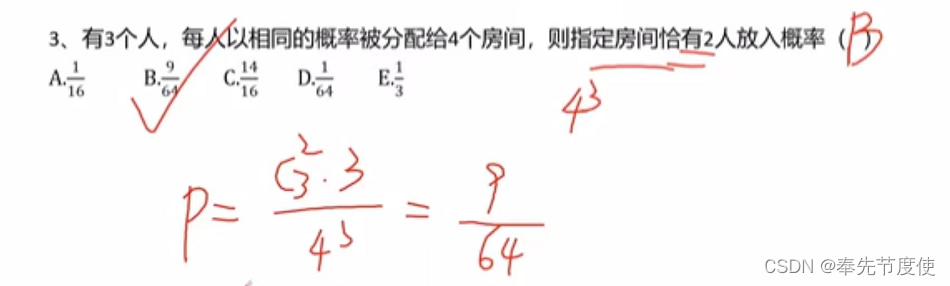
古典概型定义与分类








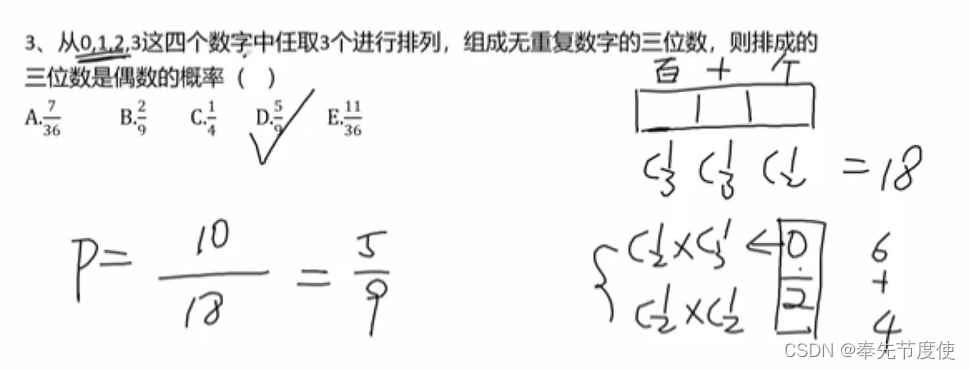
独立事件




独立重复试验/贝努力公式


数据描述(平均1题)
均值与方差









应用题(平均5题)
比例问题
- 按比例分配:把一个数按照一定比分成若干份
- 百分数问题:表示一个数是另一个数的百分之几的数
利润问题
- 利润=售价-进价(成本)
- 利润率=利润/进价=(售价-进价)/进价
- 售价=进价*(1+利润率)【即售价是进价的(1+利润率)倍,盈亏对应利润率的正负】
工程问题
- 主要分析工作量、工作效率和工作时间三者之间关系
- 工作量=工作时间*工作效率(工作量未说明时当做1)
- 工作时间=工作量/(甲工作效率+乙工作效率+xxx工作效率...)
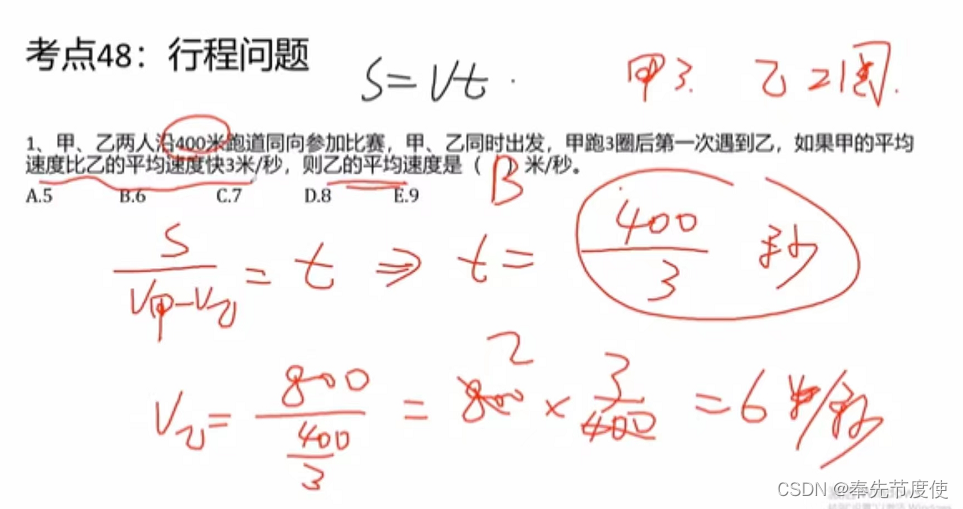
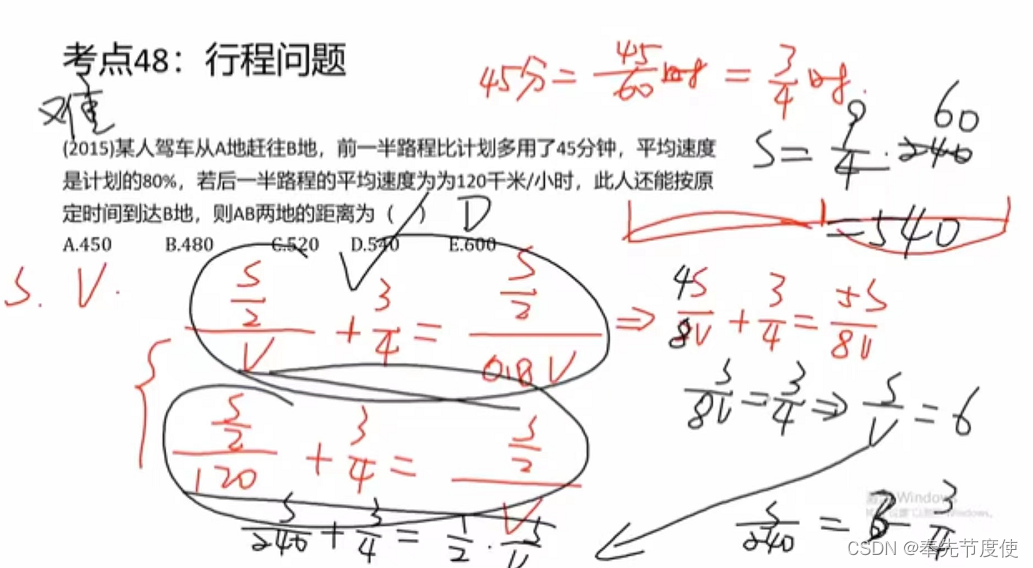
行程问题
相遇问题
- 两个运动物体同时由两地出发相向而行在途中相遇
- 解题思路为根据如下公式找等量关系,优先设速度
- 相遇时间=总路程/速度(如v甲+v乙)
- 总路程=速度和(如v甲+v乙) * 相遇时间
追击问题(环形追击时,每追上一次则多跑一圈)
- 两个运动物体作同向运动,在一定时间内后面物体追上前面物体
- 解题思路为根据如下公式找等量关系
- 追击时间=追击路程/速度(快速-慢速)
- 追击路程=速度(快速-慢速)*追击时间
列车问题
- 列车行驶运动要考虑列车车身长度
- 解题思路为根据如下公式找等量关系
- 火车过桥:过桥时间=(车长+桥长) / 车速
- 火车追击:追击时间=(甲车长+乙车长+距离) /(甲车速-乙车速)
- 火车相遇:相遇时间=(甲车长+乙车长+距离) /(甲车速+乙车速)
行船问题
- 船只航行问题,需要注意船速和水速,顺水航行时速度为船速和水速之和,逆水航行时速度为船速与水速之差
- 解题思路为根据如下公式找等量关系
- V顺水 = V船 + V水
- V逆水 = V船 - V水
- (V顺水 + V逆水) / 2 = 船速
- (V顺水 - V逆水) / 2 = 水速
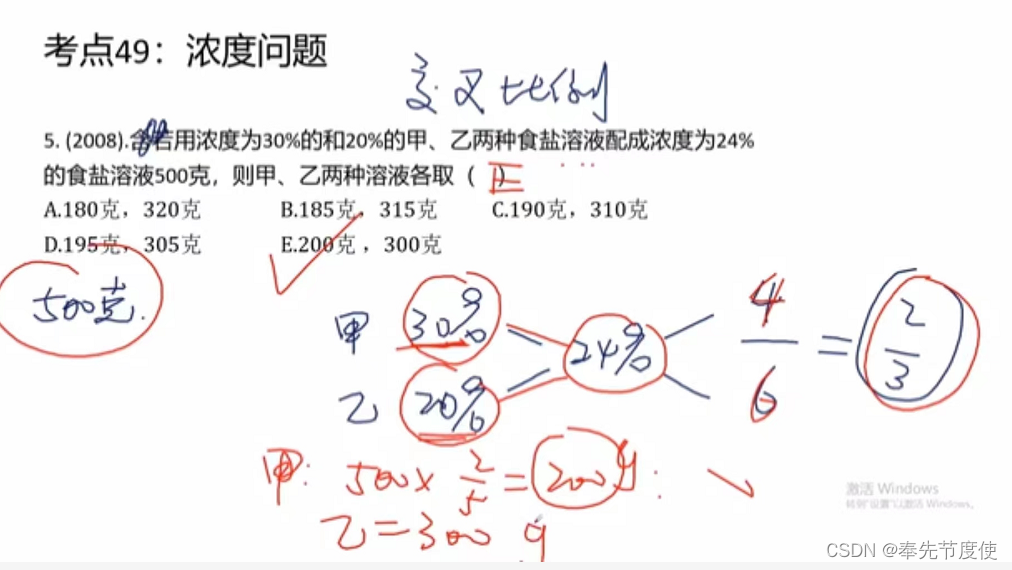
浓度问题
- 溶剂、溶质、溶液以及浓度的关系
- 根据如下公式找等量关系
- 溶液=溶剂+溶质(核心溶质不会变)
- 浓度=溶质/溶液*100%(核心溶质不会变)

最值问题
- 实际生活中,经常追求以最小的代价取得最大的效果或效益,即最值问题
- 表现形式就是根据方程求最大值或最小值
- 二次函数方f(x)=ax2 + bx + c模型,利用开口和对称轴(x=-b/2a)求最值
- a>0开口向上,有最小值,反之开口向下有最大值
- 若知道二次函数根,则直接取两根中点处为最值
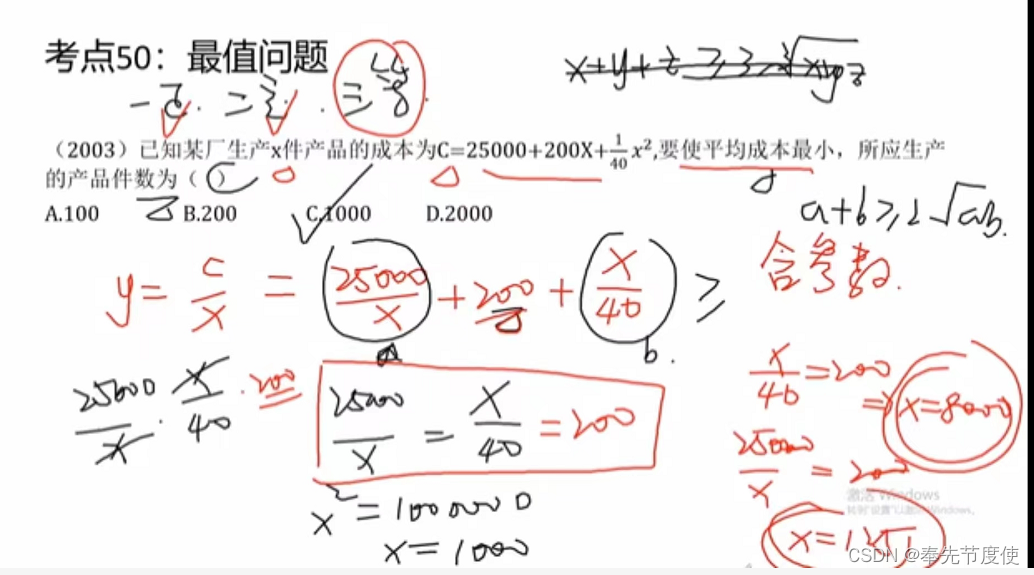
- 均值不等式模型,利用均值不等式求最值
- x2+y2>=2xy
- x + y >=2根号下xy
- 当且仅当x=y时等号成立
- 一正(x>0,y>0),二定(即x+y或xy为定值),三相等(x=y才会取到最值)
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1060777.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!