1.求偏导的自变量的符号区别
使用标量、向量和矩阵总共有九种可能性。请注意,当我们考虑每个自变量和因变量中更多数量的分量时,我们可能会留下非常多的可能性。下表收集了最能以矩阵形式最整齐地组织的六种导数。
在这里,我们使用了最一般意义上的术语“矩阵”,认识到向量和标量只是分别具有一列和一行的矩阵。此外,我们使用粗体字母表示向量,使用粗体大写字母表示矩阵。此表示法自始至终使用。
请注意,我们还可以讨论向量相对于矩阵的导数,或者我们表中的任何其他未填充单元格。然而,这些导数最自然地组织在秩高于2的张量中,因此它们不能整齐地拟合到矩阵中。在以下三节中,我们将定义这些导数中的每一个,并将它们与数学的其他分支联系起来。有关更详细的表格,请参阅布局约定部分。(摘自维基百科)
所以说向量对矩阵,矩阵对向量,矩阵对矩阵的导数尚无统一的看法,不过我们可以根据我们的需要对他们进行定义;
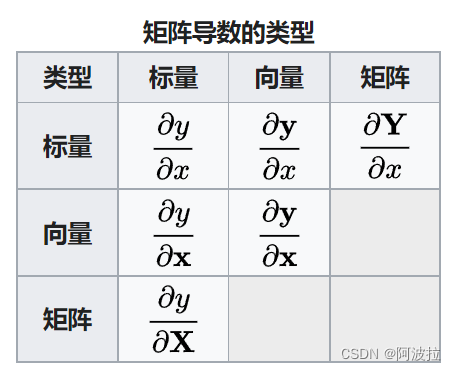
2.分子布局与分母布局
维度为m的一个向量𝐲对一个标量𝑥的求导,那么结果也是一个m维的向量:∂𝐲/∂𝑥。这个m维的求导结果排列成的m维向量到底应该是列向量还是行向量?
这个问题的答案是:
行向量或者列向量皆可! 毕竟我们求导的本质只是把标量求导的结果排列起来,至于是按行排列还是按列排列都是可以的。但是这样也有问题,在我们机器学习算法法优化过程中,如果行向量或者列向量随便写,那么结果就不唯一,乱套了。
为了解决矩阵向量求导的结果不唯一,我们引入求导布局。最基本的求导布局有两个:分子布局(numerator layout)和分母布局(denominator layout )。对于分子布局来说,我们求导结果的维度以分子为主,比如对于我们上面对标量求导的例子,结果的维度和分子的维度是一致的。对于分母布局来说,我们求导结果的维度以分母为主。
但是在机器学习算法原理的资料推导里,我们并没有看到说正在使用什么布局,也就是说布局被隐含了,这就需要自己去推演,比较麻烦。但是一般来说我们会使用一种叫混合布局的思路,即如果是向量或者矩阵对标量求导,则使用分子布局为准,如果是标量对向量或者矩阵求导,则以分母布局为准。对于向量对对向量求导,有些分歧,按分子布局的向量对向量求导的结果矩阵,我们一般叫做雅克比 (Jacobian)矩阵。按分母布局的向量对向量求导的结果矩阵,我们一般叫做梯度矩阵。
3.分子布局与分母布局
引用蒲公英书背后的数学基础里矩阵微积分章节所说的一段话开始我们的话题:
矩阵微积分的表示通常有两种符号约定:分子布局( Numerator Layout )和分母布局( Denominator Layout ).两者的区别是一个标量关于一个向量的导数是写成列向量还是行向量。(除特别说明外,本书默认采用分母布局.)
按照笔者的理解时是这样的,一般情况下:
- 分子布局:偏导后得出的矩阵是和分子的维度是一致的;
- 分母布局:偏导后得出的矩阵是和分母的维度是一致的;
而我们很多资料好像都是默认利用分母布局来进行算的,因为这样更多的使我们的结果也会成为列向量的形式(我们的自变量往往定义成列向量的形式),同时这样也更有利于我们去理解实值函数相对于实向量的求偏导:逐次对实向量每个元素求偏导,这样得到的结果自然和实向量的维度是一致的;
但是我们仍需注意到两个问题(摘自维基)
- 尽管使用了术语“分子布局”和“分母布局”,但实际上涉及两个以上的可能的符号选择。原因是分子与分母(或在某些情况下,分子与混合)的选择可以独立地用于标量按向量,逐标量,向量逐向量和标量矩阵导数,并且许多作者以各种方式混合和匹配其布局选择。
- 在下面的介绍部分中选择分子布局并不意味着这是“正确”或“优越”的选择。各种布局类型有优点和缺点。严重错误可能是由于不小心组合在不同布局中编写的公式,并且从一个布局转换为另一个布局需要小心避免错误。因此,在使用现有公式时,最佳策略可能是确定所使用的布局并保持其一致性,而不是尝试在所有情况下都使用相同的布局。
就是指我们更应该注意作者的真实意图或者使“混合布局”,而我们使用时也非常建议保持一致性;
参考资料:矩阵求导的本质与分子布局、分母布局的本质(矩阵求导——本质篇) - 知乎
https://www.cnblogs.com/Linkdom/p/16183282.html#tid-cX4btK