99％的预期缺口[…]与99.6％的[…]风险值非常接近

受到“ 瑞士经验”报告中一句话的启发，

在99％置信水平[...]上的预期缺口[…]对应于大约99.6％至99.8％的风险价值

最近我们被客户要求撰写关于VaR的研究报告，包括一些图形和统计输出。

视频：风险价值VaR原理与Python蒙特卡罗Monte Carlo模拟计算投资组合实例

，时长10:03

回顾

对于任何（绝对）连续累积分布函数，严格增加，因为（VaR和TVaR）都是连续的，并且严格增加，所以可以将任何TVaR与某个VaR关联在一起 。即

 与

考虑例如对数正态分布。由于没有关于预期短缺的简单表达式，因此 使用蒙特卡洛模拟对其进行近似。然后，使用累积分布函数获取风险值的关联级别，

> n=1e7
> TVaR_VaR_LN=function(p){
+     X=rlnorm(n)
+     E=mean(X[X>qlnorm(p)])
+     return(plnorm(E))
+ }

例如

> TVaR_VaR_LN(.99)
[1] 0.9967621

为了绘制它，定义

> prob=c(seq(.8,.99,by=.01),.995)
> P_ln=unlist(lapply(prob,TVaR_VaR_LN))

现在，如果考虑尾巴较轻的分布，例如指数分布

> P_exp=unlist(lapply(prob,TVaR_VaR_exp))

或厚尾的分布（如帕累托）

我们有不同的概率水平。

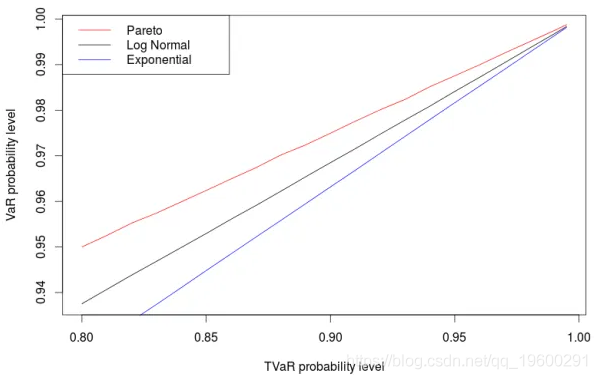
因此，尾部越重，概率水平越高。因此，在某些情况下，始终用99.6％VaR qppfoximate 99％TVaR可能有效，例如

> TVaR_VaR_exp(.99)
[1] 0.9963071