6.3 许尔估计
任意方阵 A = ( a i j ) n × n A=(a_{ij})_{n\times n} A=(aij)n×n ,全体根 λ ( A ) = { λ 1 , ⋯ , λ n } \lambda(A)=\{\lambda_1,\cdots,\lambda_n\} λ(A)={λ1,⋯,λn} ,满足 ∣ λ 1 ∣ 2 + ⋯ + ∣ λ n ∣ 2 ≤ ∑ ∣ a i j ∣ 2 \vert \lambda_1\vert^2+\cdots+\vert \lambda_n\vert^2\le \sum \vert a_{ij}\vert^2 ∣λ1∣2+⋯+∣λn∣2≤∑∣aij∣2
- 若 ∣ λ 1 ∣ 2 + ⋯ + ∣ λ n ∣ 2 = ∑ ∣ a i j ∣ 2 \vert \lambda_1\vert^2+\cdots+\vert \lambda_n\vert^2= \sum \vert a_{ij}\vert^2 ∣λ1∣2+⋯+∣λn∣2=∑∣aij∣2 ,则A为正规阵
证明
用许尔公式,存在
U
阵
Q
,使
Q
H
A
Q
=
D
=
(
λ
1
⋯
∗
⋮
⋱
⋮
0
⋯
λ
n
)
为上三角
⇒
Q
H
A
H
Q
=
D
H
,
∴
Q
H
A
H
A
Q
=
Q
H
A
H
Q
Q
H
A
Q
=
D
H
D
由于
Q
是
U
阵,则
Q
−
1
=
Q
H
,
则
Q
−
1
A
H
A
Q
=
D
H
D
,
即
A
H
A
相似于
D
H
D
故
t
r
(
A
H
A
)
=
t
r
(
D
H
D
)
而
t
r
(
A
H
A
)
=
∑
i
=
0
,
j
=
0
n
∣
a
i
j
∣
2
,
D
H
D
=
(
λ
1
‾
⋯
0
⋮
⋱
⋮
∗
‾
⋯
λ
n
‾
)
(
λ
1
⋯
∗
⋮
⋱
⋮
0
⋯
λ
n
)
故
t
r
(
D
H
D
)
=
λ
1
‾
λ
1
+
⋯
+
λ
n
‾
λ
n
+
∗
‾
∗
=
∑
k
=
0
n
∣
λ
k
∣
2
+
∑
∣
∗
∣
2
⇒
∑
i
=
0
,
j
=
0
n
∣
a
i
j
∣
2
=
∑
k
=
0
n
∣
λ
k
∣
2
+
∑
∣
∗
∣
2
≥
∑
k
=
0
n
∣
λ
k
∣
2
−
−
−
−
当
=
成立时,有
∑
∣
∗
∣
2
=
0
,故
Q
H
A
Q
=
D
=
(
λ
1
⋯
0
⋮
⋱
⋮
0
⋯
λ
n
)
为对角阵(正规阵),
则
A
为正规阵
\begin{aligned} &用许尔公式,存在U阵Q,使Q^HAQ=D=\left( \begin{matrix} \lambda_1&\cdots&*\\ \vdots&\ddots&\vdots\\ 0&\cdots&\lambda_n \end{matrix} \right) 为上三角\\ &\Rightarrow Q^HA^HQ=D^H,\quad \therefore Q^HA^HAQ=Q^HA^HQQ^HAQ=D^HD\\ &由于Q是U阵,则Q^{-1}=Q^H,则Q^{-1}A^HAQ=D^HD,即A^HA相似于D^HD\\ &故tr(A^HA)=tr(D^HD)\\ &而tr(A^HA)=\sum_{i=0,j=0}^n\vert a_{ij}\vert^2,D^HD=\left( \begin{matrix} \overline{\lambda_1}&\cdots&0\\ \vdots&\ddots&\vdots\\ \overline{*}&\cdots&\overline{\lambda_n} \end{matrix} \right)\left( \begin{matrix} \lambda_1&\cdots&*\\ \vdots&\ddots&\vdots\\ 0&\cdots&\lambda_n \end{matrix} \right)\\ &故tr(D^HD)=\overline{\lambda_1}\lambda_1+\cdots+\overline{\lambda_n}\lambda_n+\overline{*}*=\sum_{k=0}^n\vert \lambda_k\vert^2+\sum\vert *\vert^2\\ &\Rightarrow \sum_{i=0,j=0}^n\vert a_{ij}\vert^2=\sum_{k=0}^n\vert \lambda_k\vert^2+\sum\vert *\vert^2\ge \sum_{k=0}^n\vert \lambda_k\vert^2\\ &----\\ &当 = 成立时,有 \sum \vert *\vert^2=0 ,故 Q^HAQ=D=\left( \begin{matrix} \lambda_1&\cdots&0\\ \vdots&\ddots&\vdots\\ 0&\cdots&\lambda_n \end{matrix}\right)为对角阵(正规阵),\\ &则A为正规阵 \end{aligned}
用许尔公式,存在U阵Q,使QHAQ=D=
λ1⋮0⋯⋱⋯∗⋮λn
为上三角⇒QHAHQ=DH,∴QHAHAQ=QHAHQQHAQ=DHD由于Q是U阵,则Q−1=QH,则Q−1AHAQ=DHD,即AHA相似于DHD故tr(AHA)=tr(DHD)而tr(AHA)=i=0,j=0∑n∣aij∣2,DHD=
λ1⋮∗⋯⋱⋯0⋮λn
λ1⋮0⋯⋱⋯∗⋮λn
故tr(DHD)=λ1λ1+⋯+λnλn+∗∗=k=0∑n∣λk∣2+∑∣∗∣2⇒i=0,j=0∑n∣aij∣2=k=0∑n∣λk∣2+∑∣∗∣2≥k=0∑n∣λk∣2−−−−当=成立时,有∑∣∗∣2=0,故QHAQ=D=
λ1⋮0⋯⋱⋯0⋮λn
为对角阵(正规阵),则A为正规阵
eg

∣ λ I − A ∣ = λ 3 − a 1 a 2 a 3 = 0 ⇒ λ = a 1 a 2 a 3 3 , ∑ ∣ λ ∣ 2 = 3 ( a 1 a 2 a 3 ) 2 3 ∑ ∣ a i j ∣ = a 1 2 + a 2 2 + a 3 2 , 由许尔估计, ∑ ∣ a i j ∣ ≥ ∑ ∣ λ ∣ 2 当且仅当 a 1 = a 2 = a 3 时,有 ∑ ∣ a i j ∣ = ∑ ∣ λ ∣ 2 , 即 A 为正规阵 \begin{aligned} &\vert \lambda I-A\vert=\lambda^3-a_1a_2a_3=0\Rightarrow \lambda=\sqrt[3]{a_1a_2a_3},\sum\vert \lambda\vert^2=3(a_1a_2a_3)^{\frac{2}{3}}\\ &\sum\vert a_{ij}\vert=a_1^2+a_2^2+a_3^2,由许尔估计, \sum\vert a_{ij}\vert\ge \sum\vert \lambda\vert^2\\ &当且仅当 a_1=a_2=a_3时,有 \sum\vert a_{ij}\vert= \sum\vert \lambda\vert^2,即A为正规阵 \end{aligned} ∣λI−A∣=λ3−a1a2a3=0⇒λ=3a1a2a3,∑∣λ∣2=3(a1a2a3)32∑∣aij∣=a12+a22+a32,由许尔估计,∑∣aij∣≥∑∣λ∣2当且仅当a1=a2=a3时,有∑∣aij∣=∑∣λ∣2,即A为正规阵

∣ λ I − A ∣ = λ n − ( − 1 ) n ∏ i = 1 n a i = 0 , λ i = − ∏ i = 1 n a i n , ∴ 有许尔估计 ∑ i = 1 n ∣ λ i ∣ 2 = n ( ∏ i = 1 n a i ) 2 n ≤ ∑ i = 1 n a i 2 当且仅当 a 1 = ⋯ = a n 时,满足 A H A = A A H , A 为正规阵 \begin{aligned} &\vert \lambda I-A\vert=\lambda^n-(-1)^{n}\prod_{i=1}^na_i=0,\lambda_i=-\sqrt[n]{\prod_{i=1}^na_i},\\ &\therefore 有许尔估计\sum_{i=1}^n\vert \lambda_i\vert^2=n(\prod_{i=1}^na_i)^{\frac{2}{n}}\le \sum_{i=1}^na_i^2\\ &当且仅当a_1=\cdots=a_n时,满足A^HA=AA^H,A为正规阵 \end{aligned} ∣λI−A∣=λn−(−1)ni=1∏nai=0,λi=−ni=1∏nai,∴有许尔估计i=1∑n∣λi∣2=n(i=1∏nai)n2≤i=1∑nai2当且仅当a1=⋯=an时,满足AHA=AAH,A为正规阵
6.4 谱(特征值)估计
6.4.1 盖尔圆定理1:A的全体特征根被 n个Ger圆盖住
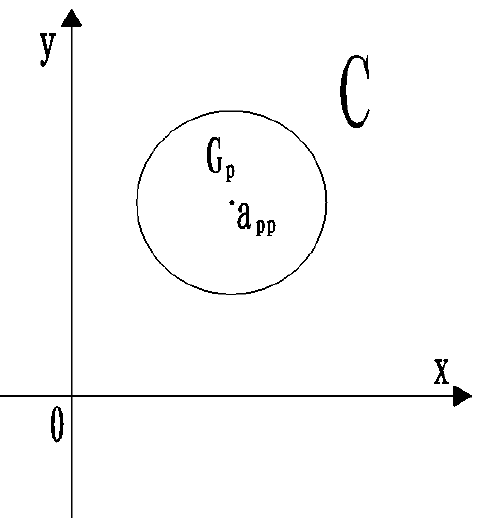
a. Ger圆盘
n 阶方阵 A = ( a i j ) n × n A=(a_{ij})_{n\times n} A=(aij)n×n 的第i个Ger半径为 R i = ∑ i = 1 , j ≠ i n ∣ a i j ∣ = ∣ a i 1 ∣ + ⋯ + ∣ a i i − 1 ∣ + ∣ a i i + 1 ∣ + ⋯ + ∣ a i n ∣ R_i=\sum_{i=1,j\neq i}^{n}\limits \vert a_{ij}\vert = \vert a_{i1}\vert+\cdots+\vert a_{ii-1}\vert+\vert a_{ii+1}\vert+\cdots+\vert a_{in}\vert Ri=i=1,j=i∑n∣aij∣=∣ai1∣+⋯+∣aii−1∣+∣aii+1∣+⋯+∣ain∣ ,规定第i个Ger圆为 G i = { Z ∣ ∣ Z − a i i ∣ ≤ R i } , Z ∈ C , i = 1 , 2 , ⋯ , n G_i=\{Z\mid \vert Z-a_{ii}\vert\le R_i\},Z\in C,i=1,2,\cdots,n Gi={Z∣∣Z−aii∣≤Ri},Z∈C,i=1,2,⋯,n
b. 圆盘定理
方阵 A = ( a i j ) n × n A=(a_{ij})_{n\times n} A=(aij)n×n 的全体特征根都在A的n个Ger圆盘并集内,即 λ ( A ) = { λ 1 , ⋯ , λ n } ⊂ G 1 ∪ G 2 ∪ ⋯ ∪ G n = ⋃ i = 1 n G i = Δ G ( A ) \lambda(A)=\{\lambda_1,\cdots,\lambda_n\}\subset G_1\cup G_2\cup\cdots\cup G_n=\bigcup_{i=1}^{n}\limits G_i \overset{\Delta}{=}G(A) λ(A)={λ1,⋯,λn}⊂G1∪G2∪⋯∪Gn=i=1⋃nGi=ΔG(A)
即 Ger 圆盘并集 G ( A ) G(A) G(A) 覆盖了全体特征根 λ ( A ) ⊂ G ( A ) \lambda(A)\subset G(A) λ(A)⊂G(A) ,A的全体特征根被 n个Ger圆盖住
eg
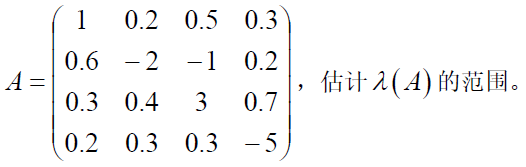
Ger圆为 G 1 : ∣ Z − a 11 ∣ = ∣ Z − 1 ∣ ≤ R 1 = 0.2 + 0.5 + 0.3 = 1 G 2 : ∣ Z − a 22 ∣ = ∣ Z − ( − 2 ) ∣ ≤ R 2 = 0.6 + 1 + 0.2 = 1.8 G 3 : ∣ Z − a 33 ∣ = ∣ Z − ( 3 ) ∣ ≤ R 3 = 0.3 + 0.4 + 0.7 = 1.4 G 4 : ∣ Z − a 44 ∣ = ∣ Z − ( − 5 ) ∣ ≤ R 4 = 0.2 + 0.3 + 0.3 = 0.8 \begin{aligned}&G_1:\vert Z-a_{11}\vert=\vert Z-1\vert\le R_1=0.2+0.5+0.3=1\\ &G_2:\vert Z-a_{22}\vert = \vert Z-(-2)\vert\le R_2=0.6+1+0.2=1.8\\ &G_3:\vert Z-a_{33}\vert = \vert Z-(3)\vert\le R_3=0.3+0.4+0.7=1.4\\ &G_4:\vert Z-a_{44}\vert = \vert Z-(-5)\vert\le R_4=0.2+0.3+0.3=0.8\\\end{aligned} G1:∣Z−a11∣=∣Z−1∣≤R1=0.2+0.5+0.3=1G2:∣Z−a22∣=∣Z−(−2)∣≤R2=0.6+1+0.2=1.8G3:∣Z−a33∣=∣Z−(3)∣≤R3=0.3+0.4+0.7=1.4G4:∣Z−a44∣=∣Z−(−5)∣≤R4=0.2+0.3+0.3=0.8
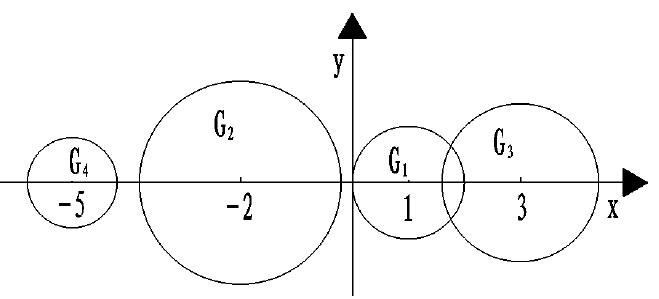
λ ( A ) ⊂ G 1 ∪ G 2 ∪ G 3 ∪ G 4 \lambda(A)\subset G_1\cup G_2 \cup G_3 \cup G_4 λ(A)⊂G1∪G2∪G3∪G4
6.4.2 圆盘定理2:连通分支
若A的k个 Ger 圆相连(相切),且与其他 n − k n-k n−k 个圆分离,称此 k k k 个圆的并集为一个连通分支,简称分支
- 一个孤立圆盘是一个分支
设D是A的k个 Ger圆构成的分支,则D中恰有k个特征值(含重复)
如上述 G 1 G_1 G1 和 G 3 G_3 G3 为一个连通分支 , G 2 G_2 G2 、 G 4 G_4 G4 分别为一个分支,且A至少有2个实特征根
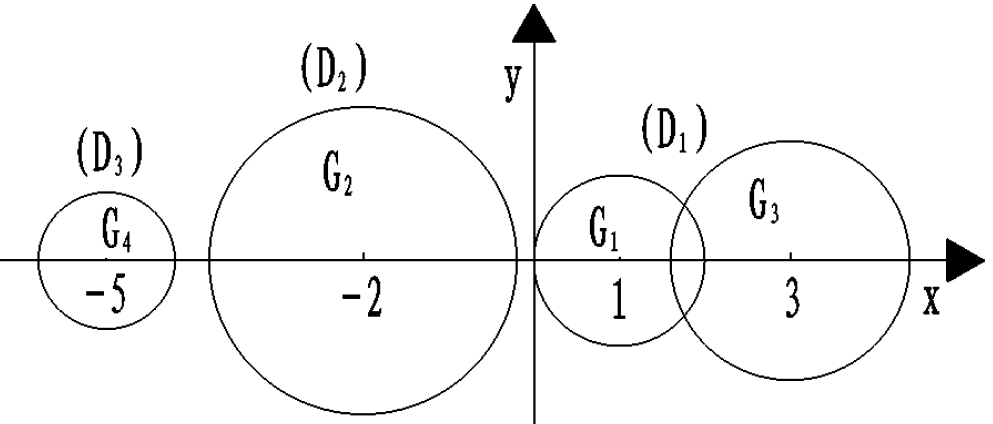
- 独立圆盘必定包含一个实根,虚根必然成对出现在同一连通分支
eg
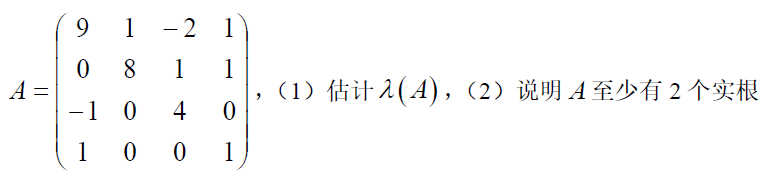
G
1
:
∣
Z
−
a
11
∣
=
∣
Z
−
9
∣
≤
R
1
=
1
+
2
+
1
=
4
G
2
:
∣
Z
−
a
22
∣
=
∣
Z
−
8
∣
≤
R
2
=
1
+
1
=
2
G
3
:
∣
Z
−
a
33
∣
=
∣
Z
−
4
∣
≤
R
3
=
1
G
4
:
∣
Z
−
a
44
∣
=
∣
Z
−
1
∣
≤
R
4
=
1
\begin{aligned} &G_1:\vert Z-a_{11}\vert=\vert Z-9\vert\le R_1=1+2+1=4\\ &G_2:\vert Z-a_{22}\vert=\vert Z-8\vert\le R_2=1+1=2\\ &G_3:\vert Z-a_{33}\vert=\vert Z-4\vert\le R_3=1\\ &G_4:\vert Z-a_{44}\vert=\vert Z-1\vert\le R_4=1\\ \end{aligned}
G1:∣Z−a11∣=∣Z−9∣≤R1=1+2+1=4G2:∣Z−a22∣=∣Z−8∣≤R2=1+1=2G3:∣Z−a33∣=∣Z−4∣≤R3=1G4:∣Z−a44∣=∣Z−1∣≤R4=1
G
4
G_4
G4 为一个分支
D
1
D_1
D1,
G
3
、
G
2
、
G
1
G_3、G_2、G_1
G3、G2、G1 为一个分支
D
2
D_2
D2。 由于虚根是成对出现的,且
D
1
D_1
D1 中只有一个特根,
D
2
D_2
D2 中有3个特根,故
D
1
D_1
D1 中的特根一定是实根,
D
2
D_2
D2 至少有一个实根
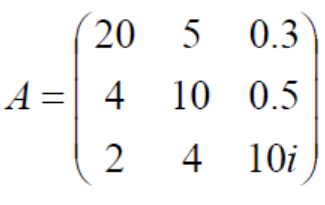
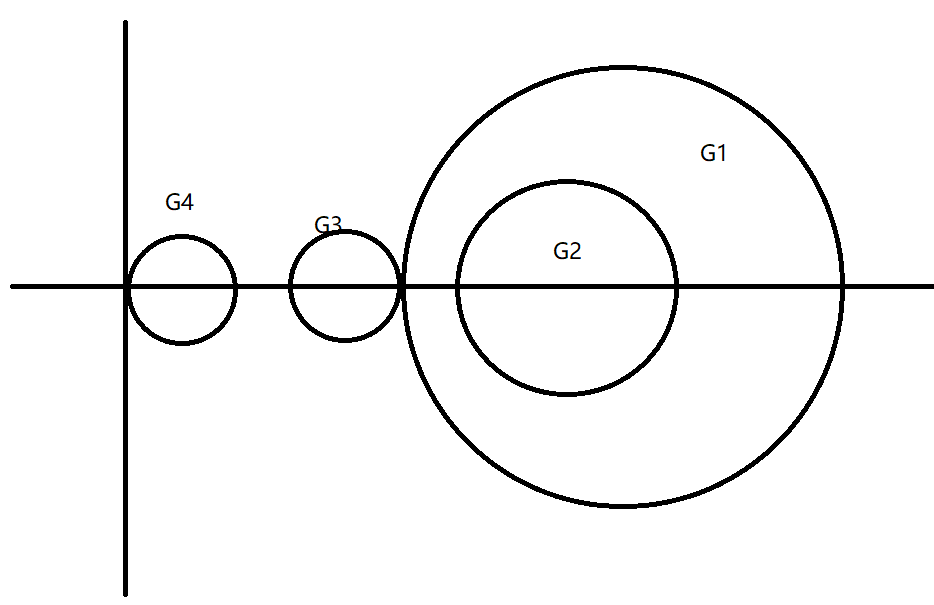
G
1
:
∣
Z
−
a
11
∣
=
∣
Z
−
20
∣
≤
R
1
=
5.3
G
2
:
∣
Z
−
a
22
∣
=
∣
Z
−
10
∣
≤
R
2
=
4.5
G
3
:
∣
Z
−
a
33
∣
=
∣
Z
−
10
i
∣
≤
R
3
=
6
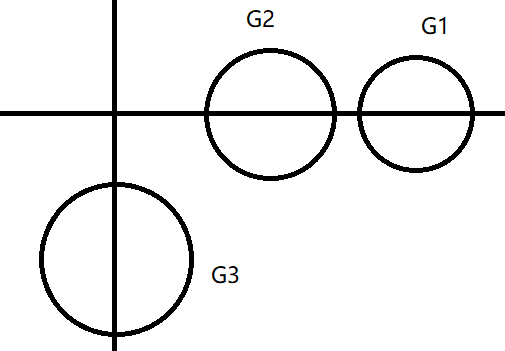
\begin{aligned} &G_1:\vert Z-a_{11}\vert=\vert Z-20\vert\le R_1=5.3\\ &G_2:\vert Z-a_{22}\vert=\vert Z-10\vert\le R_2=4.5\\ &G_3:\vert Z-a_{33}\vert=\vert Z-10i\vert\le R_3=6 \end{aligned}
G1:∣Z−a11∣=∣Z−20∣≤R1=5.3G2:∣Z−a22∣=∣Z−10∣≤R2=4.5G3:∣Z−a33∣=∣Z−10i∣≤R3=6
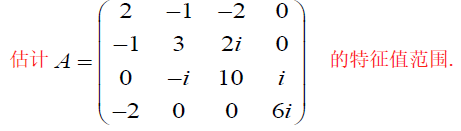

6.4.3 许尔圆盘推论
a. 原点不在圆盘内,则A可逆
对方阵 A,若原点 0 ∉ G ( A ) 0\notin G(A) 0∈/G(A) ,即 0 0 0 在n个Ger圆之外,则A为可逆阵
反证: 若 0 ∉ G ( A ) , 且 A 不可逆,则 ∣ A ∣ = ∏ i = 0 n λ i = 0 , 即 0 ∈ λ ( A ) , 故 0 ∈ ⋃ i = 0 n G i ,矛盾 故方阵 A ,若原点 0 ∉ G ( A ) ,则 A 可逆 \begin{aligned} &反证:\\ &若0\notin G(A),且A不可逆,则 \vert A\vert =\prod_{i=0}^{n}\lambda_i=0,即0\in \lambda(A),故0\in \bigcup_{i=0}^nG_i ,矛盾\\ &故方阵A,若原点 0 \notin G(A),则A可逆 \end{aligned} 反证:若0∈/G(A),且A不可逆,则∣A∣=i=0∏nλi=0,即0∈λ(A),故0∈i=0⋃nGi,矛盾故方阵A,若原点0∈/G(A),则A可逆
b. 对角占优阵一定可逆
若 A = ( a i j ) n , n A=(a_{ij})_{n,n} A=(aij)n,n 为行对角占优阵,则A可逆
若 A = ( a i j ) n , n A=(a_{ij})_{n,n} A=(aij)n,n 为列对角占优阵,则A可逆
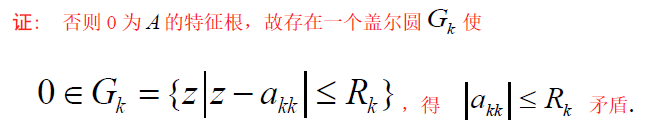
c. k个分离Ger圆,则有k个不同根
若 A ∈ C n × n A\in C^{n\times n} A∈Cn×n 的n个Ger圆中有k个独立的Ger圆,则A至少有k个互异特征根
- 若A的n个Ger圆互相分离(都是孤立圆),则A是单阵(可对角化)
若实对称阵
A
∈
C
n
×
n
A\in C^{n\times n}
A∈Cn×n 的n个Ger圆中有k个独立的Ger圆,则A至少有k个互异实特征根
A
的
n
个
G
e
r
圆圆心都在实轴上,故每个孤立
G
e
r
圆中只能有一个特征值
实对称阵
A
若有复根,必共轭出现,故
G
e
r
圆中的特征值必为实特征值
A的n个Ger圆圆心都在实轴上,故每个孤立Ger圆中只能有一个特征值\\ 实对称阵A若有复根,必共轭出现,故Ger圆中的特征值必为实特征值
A的n个Ger圆圆心都在实轴上,故每个孤立Ger圆中只能有一个特征值实对称阵A若有复根,必共轭出现,故Ger圆中的特征值必为实特征值
eg
R 1 = R 2 = R 3 = 3 4 , , 3 个 G e r 圆为 ∣ Z − 3 ∣ ≤ 3 4 , ∣ Z − 1 ∣ ≤ 3 4 , ∣ Z − 5 ∣ ≤ 3 4 \begin{aligned} &R_1=R_2=R_3=\frac{3}{4},,3个Ger圆为 \vert Z-3\vert\le \frac{3}{4},\vert Z-1\vert\le \frac{3}{4},\vert Z-5\vert\le \frac{3}{4}\\ \end{aligned} R1=R2=R3=43,,3个Ger圆为∣Z−3∣≤43,∣Z−1∣≤43,∣Z−5∣≤43
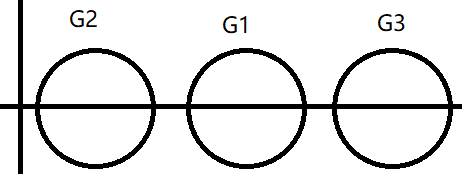
可见3个Ger圆中心在x轴上,都是独立的圆,故A有3个不同特根,A为单阵
且 λ ≥ 1 − 3 4 , λ 2 ≥ 3 − 3 4 , λ 3 ≥ 5 − 3 4 , ⇒ ∣ A ∣ ≥ 1 4 ⋅ 9 4 ⋅ 17 4 = 9 × 17 64 \lambda\ge 1-\frac{3}{4},\lambda_2\ge 3-\frac{3}{4},\lambda_3\ge 5-\frac{3}{4},\Rightarrow \vert A\vert\ge \frac{1}{4}\cdot\frac{9}{4}\cdot\frac{17}{4}=\frac{9\times 17}{64} λ≥1−43,λ2≥3−43,λ3≥5−43,⇒∣A∣≥41⋅49⋅417=649×17
d. A A A 与 A T A^T AT 的Ger圆
由于A与 A T A^T AT 有相同特征值, λ ( A ) = λ ( A T ) \lambda(A)=\lambda(A^T) λ(A)=λ(AT),可用 A的Ger半径代替 A T 的 G e r 半径 A^T的Ger半径 AT的Ger半径
A的列圆盘定理:A的列圆盘为 G p ′ = { Z ∣ ∣ Z − a p p ∣ ≤ R p ~ } , p = 1 , 2 , ⋯ , n G_p'=\{Z|\vert Z-a_{pp}\vert\le \widetilde{R_p}\},p=1,2,\cdots,n Gp′={Z∣∣Z−app∣≤Rp },p=1,2,⋯,n ,其中 R p ~ = ∣ a 1 p ∣ + ⋯ + ∣ a p − 1 p ∣ + ∣ a p + 1 p ∣ + ⋯ + ∣ a n p ∣ \widetilde{R_p}=\vert a_{1p}\vert+\cdots+\vert a_{p-1p}\vert+\vert a_{p+1p}\vert+\cdots+\vert a_{np}\vert Rp =∣a1p∣+⋯+∣ap−1p∣+∣ap+1p∣+⋯+∣anp∣ 为列半径
对于 A T A^T AT 的Ger圆 G 1 ′ , G 2 ′ , ⋯ , G n ′ G_1',G_2',\cdots,G_n' G1′,G2′,⋯,Gn′ 与 A A A 的Ger圆 G 1 , G 2 , ⋯ , G n G_1,G_2,\cdots,G_n G1,G2,⋯,Gn 有相同的圆心,故特征值 λ i ∈ ( ⋃ i = 1 n G i ) ⋂ ( ⋃ i = 1 n G i ′ ) , 1 ≤ i ≤ n \lambda_i\in (\bigcup_{i=1}^{n}\limits G_i)\bigcap(\bigcup_{i=1}^{n}\limits G_i'),1\le i\le n λi∈(i=1⋃nGi)⋂(i=1⋃nGi′),1≤i≤n