Leetcode 4.寻找两个正序数组的中位数
题目描述:
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
解法1:先排序再查找
先将两个数组进行合并以及排序,此时就是题目就变得很简单了,但是排序的时间复杂度为O((m+n)log(m+n),是不符合题意的。
解法2:暴力解法
通过上面的方法,发现只需要排序到中位数的位置即可,没有必要将所有的元素进行排序。因此可以对两个数组的头元素进行一一比较,元素较小的数组的指针指向下一位,直到指向我们所需要的中位数位置。但是该解法的时间复杂度也高达O(m+n),不符合题目要求。
解法3:划分数组
首先,我们假设nums1的长度小于nums2的长度。
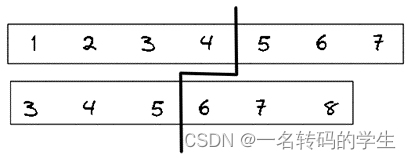
我们既然要求的是中位数,如果能够找到一条线可以使得左边和右边元素个数之和相等或者两边相差1(我们此处令左边多一个元素)。
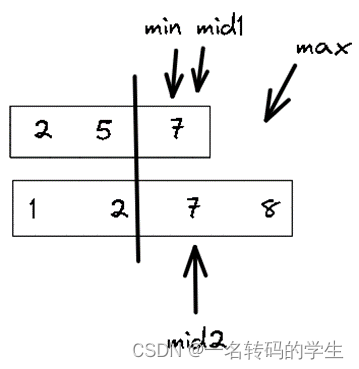
如果两个数组的元素个数之和为奇数,那么中位数就应该是左边元素的较大者,如左下图中左边元素的最大值为5。
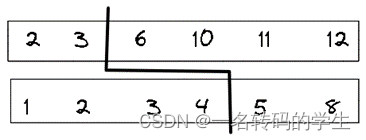
如果两个数组的元素之和为偶数,那么按照定义,中位数应该是中间两个数的平均值。在这种方法中应该是左边元素的最大值与右边元素最小值的平均值。如右上图的4和5的平均,输出应该是4.5。
同时也会出现如下极端情况,如果两数组个数之和是奇数,我们取左边存在的元素。如果是偶数,取左右两边存在的元素的平均值。

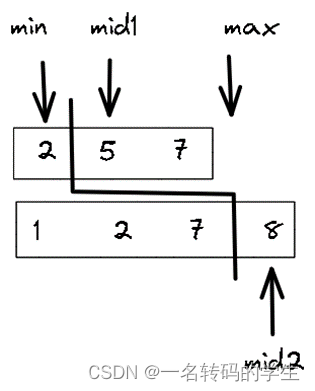
与此同时,如何找到这条线变成了当前的问题。对此可以选择二分查找。
min与max指针为左闭右开,分别指向两端,当min指针严格在max指针左侧时循环。取mid1为两指针中间位置,mid2按照定义进行计算。此时发现并没有严格满足划线左边元素小于右边元素,此时mid1太小了,我们应该让min右移,使其等于mid1+1,重新计算mid2。此时满足划线左侧小于右侧,返回左侧最大值5。
class Solution:
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
if len(nums1)>len(nums2):
# 此处也可以加一个临时变量,将nums1和nums2进行互换,保证nums2更长一点
return self.findMedianSortedArrays(nums2,nums1)
m = len(nums1)
n = len(nums2)
# 左边总共元素个数为下面所示
totalleft = (n+m+1)//2
#初始化左右指针
mi = 0
ma = m
while mi<=ma:
# 左闭右开,mid1可取到,mid2不可取到
mid1 = (ma+mi)//2
mid2 = totalleft-mid1
# 下面判断可以防止数组越界
if mid2 != 0 and mid1 != m and nums2[mid2-1] >nums1[mid1]:
mi = mid1+1
elif mid1 != 0 and mid2 !=n and nums2[mid2]<nums1[mid1-1]:
ma = mid1-1
else:
if mid1 == 0:
left = nums2[mid2-1]
elif mid2 == 0:
left = nums1[mid1-1]
else:
left = max(nums2[mid2-1],nums1[mid1-1])
if (m+n)%2 == 1:
return left
else:
if mid1 == m:
right = nums2[mid2]
elif mid2 == n:
right = nums1[mid1]
else:
right = min(nums2[mid2],nums1[mid1])
return (left+right)/2Leetcode 10.正则表达式匹配
题目描述:
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖整个字符串s的,而不是部分字符串。
解法1:动态规划
dp数组定义
我们定义动态规划的dp数组,dp数组的大小为(m+1) * (n+1),其中m是s的长度,n为p的长度。动态数组dp[i][j]表示s的前i-1个元素是否和p的前j-1个元素匹配,若为True,则表示为匹配。
dp数组初始化
而初始化dp数组时,根据其含义dp[0][0]表示两个空的位置,此时理应让两个空数组为1,表示两个空数组可以相互匹配。其次就是当p数组元素下标为j为*且dp[0][j-2]=True时(如下图),我们令dp[0][j]也为True,因为这也可以匹配空字符串。同理如果为‘ ’,也令dp[0][j-1]为True。
dp数组更新
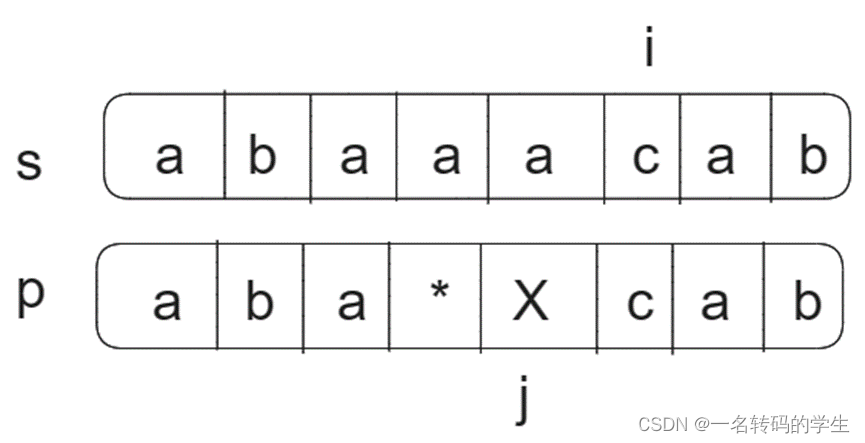
对于dp数组的更新,如果数组p的第j个字符不是‘*’:
此时如果 s 的第 i 个字符和 p 的第 j 个字符匹配,即 s[i-1] == p[j-1] 或 p[j-1] == '.',那么 dp[i][j] 等于 dp[i-1][j-1]。否则,dp[i][j] 为 False。如图所示,s的前i个元素已经和p的前j个元素匹配,如果此时p数组的p[j]中的X为‘c’或者‘.’说明dp[i+1][j+1]应该更新为True否则应该为False。
如果 p 的第 j 个字符是 '*':
如果 s 的第 i 个字符和 p 的第 j-1 个字符不匹配,那么 dp[i][j] 等于 dp[i][j-2],即 p[j-2:j-1] 匹配空字符串。
否则,dp[i][j] 等于 dp[i][j-2](即p[j-2:j-1] 匹配空字符串)、dp[i-1][j](即p[j-2:j-1] 匹配一个字符)或 dp[i-1][j-1](p[j-2:j-1] 匹配多个字符)的逻辑或运算结果,具体取决于 s 的第 i 个字符和 p 的第 j-1 个字符是否匹配。
返回结果
返回 dp[-1][-1],即 dp 数组的右下角元素,表示整个 s 和 p 是否匹配。
代码
class Solution:
def isMatch(self, s: str, p: str) -> bool:
m, n = len(s) + 1, len(p) + 1
dp = [[False] * n for _ in range(m)]
dp[0][0] = True
for j in range(2, n, 2):
dp[0][j] = dp[0][j - 2] and p[j - 1] == '*'
for i in range(1, m):
for j in range(1, n):
dp[i][j] = dp[i][j - 2] or dp[i - 1][j] and (s[i - 1] == p[j - 2] or p[j - 2] == '.') \
if p[j - 1] == '*' else \
dp[i - 1][j - 1] and (p[j - 1] == '.' or s[i - 1] == p[j - 1])
return dp[-1][-1]
解法2:回溯算法
定义回溯函数
定义一个回溯函数 backtrack(s, p, i, j),其中参数分别是原字符串 s,正则表达式 p,当前匹配的位置 i 和 j。首先判断当前位置是否遍历到了 s 和 p 的末尾。如果是的话,返回 True,表示已经匹配完成。
回溯判断
如果 p 的第 j 个字符存在 '*':
如果 s 的第 i 个字符和 p 的第 j-1 个字符匹配(即 s[i] == p[j-1] 或 p[j-1] == '.'),则可以进行两种选择:跳过该字符和 '*',即不将 p 的第 j-1 和第 j 个字符匹配到 s 中,即调用 backtrack(s, p, i, j+2)。将 p 的第 j-1 和第 j 个字符匹配到 s 中,即调用 backtrack(s, p, i+1, j)。
如果 s 的第 i 个字符和 p 的第 j-1 个字符不匹配,只能跳过该字符和 '*',即调用 backtrack(s, p, i, j+2)。
若 p 的第 j 个字符不存在 '*':
如果 s 的第 i 个字符和 p 的第 j 个字符匹配(即 s[i] == p[j] 或 p[j] == '.'),则调用 backtrack(s, p, i+1, j+1)。如果 s 的第 i 个字符和 p 的第 j 个字符不匹配,直接返回 False。
返回回溯结果
最后返回答案即可,但是算法时间复杂度会很高,会发生超时。
代码
class Solution:
def isMatch(self, s: str, p: str) -> bool:
def backtrack(s, p, i, j):
# 判断是否遍历到末尾
if i == len(s) and j == len(p):
return True
# 当 p 的第 j 个字符存在 '*' 时
if j + 1 < len(p) and p[j + 1] == '*':
if i < len(s) and (s[i] == p[j] or p[j] == '.'):
# 两种选择:跳过该字符和 '*';将该字符和 '*' 匹配到 s 中
return backtrack(s, p, i, j + 2) or backtrack(s, p, i + 1, j)
else:
# 跳过该字符和 '*'
return backtrack(s, p, i, j + 2)
# 当 p 的第 j 个字符不存在 '*' 时
if i < len(s) and j < len(p) and (s[i] == p[j] or p[j] == '.'):
return backtrack(s, p, i + 1, j + 1)
return False
return backtrack(s, p, 0, 0)