管理类考试介绍
- 管理综合200分,时间3小时
- 数学:75分/25题,是拉开差距的核心模块
- 问题求解题:15个,5选一
- 条件充分性判断:10个,结合两个条件选择答案
- 条件一充分,条件二不充分:A
- 条件一不充分,条件二充分:B
- 条件一充分,条件二充分:D
- 条件一不充分,条件二不充分,联合充分:C
- 条件一不充分,条件二不充分,联合不充分:E
- 逻辑:60分/30题,形式、论证、分析推理【大部分40-50分】
- 写作:65分/2篇作文,论证有效性分析600字,论说文700字【大部分35-45分】
- 数学:75分/25题,是拉开差距的核心模块
- 英语二 100分,3小时
数学概述
算术(平均1-2题)
有理数和无理数
实数分为有理数和无理数,两者区别在于能否写成两个整数之比
- 有理数包括整数和分数
- 整数:正整数、0、负整数
- 自然数:0和正整数统称为自然数,即非负整数
- 无理数:无限不循环小数,如e、log等
- 经常考察一个式子同时含有有理数与无理数部分,整体等于0
- 解题思路: 有理数部分合并,无理数部分合并,分别为0
质数与合数
- 质数/素数:大于1的整数,除了1和自身之外不能被其他正整数整除的数(即约数只有1和质数本身)
- 合数:大于1的整数,除了1和自身之外还能被其他正整数整除的数(即约数包括1、本身以及其他约数)
- 注意
- 1既不是质数也不是合数,2是唯一的偶质数;质因数表示既是一个数的约数又是质数的数
- 20以内8大质数:2,3,5,7,11,13,17,19
奇数偶数
- 奇数:不能被2整除的整数,表示为2k+1
- 偶数:能被2整除的整数,包括0,表示为2k
整除/约数/倍数
- 常见数整除的特征
- 能被2整除的数:个位数字为0、2、4、6、8
- 能被3整除的数:各位数字之和必能被3整除
- 能被4整除的数:末两位数字必能被4整除
- 能被5整除的数:个位数字为0或5
- 能被6整除的数:同时满足能被2和3整除
- 能被8整除的数:末三位数字必能被8整除
- 能被9整除的数:各位数字之和能被9整除
- 能被10整除的数:个位数字为0
- 公约数:几个自然数公有的约数,称为这几个自然数的公约数,公约数中最大的公约数称为这几个自然数的最大公约数
- 最小公倍数:几个自然数公有的倍数(排除0以外)

绝对值非负性
- 正数的绝对值是它本身,负数是它的相反数,零的绝对值还是0
- 几何意义:表示一个实数a在数轴上所对应的点到原点0的距离值,如|x-b| =a表示与b点的距离为a
- 非负符号:绝对值、偶次乘方、开偶次根号
- 常见考试场景:含有绝对值和开偶次根号或者偶次乘方
- 解题思路:保持各项为0即可
绝对值两个模型
- 和模型(函数曲线为平底锅型):存在最小值
- |x-a|+|x-b|几何意义表示数轴上x到a与b点的距离之和,当x在a点与b点之间存在最小值,即最小距离值为|a-b|,x不在两者之间则趋于正无穷.
- 若f(x) = |x-a|+|x-b|+|x-c|,也无最大值,当x在a与c之间时且x=b时存在最小值|c-a|
- 即奇数个点取中间点有最小值,偶数个点取中间两个数之间点有最小值
- 差模型(函数曲线为Z字型):既有最小值也存在最大值
- |x-a|-|x-b|几何意义表示数轴上x到a与b点的距离之差,当x在a点与b点之外时存在最大值|a-b|和最小距离值为-|a-b|
三角不等式(求最值)
- |a + b| <= |a|+|b|;等号成立条件ab>=0;
- |a - b| <= |a|+|b|;等号成立条件ab<=0;
- 三角不等式主要考察取等号条件,消去参数是核心
比和比例
- 比例基本性质
- 比例的前项和后项同时乘或除以不含0的相同的数,比值不变
- a:b=c:d <==> b:a=d:c<=> a:c=b:d<=>c:a=d:b
- 比例定理
- 合比定理:a/b = c/d <=> (a+b)/b=(c+d)/d
- 分比定理:a/b = c/d <=> (a-b)/b=(c-d)/d
- 合分比定理:a/b = c/d <=> (a+b)/a-b=(c+d)/c-d
- 等比定理:a/b = c/d = e/f =a+c+e/b+d+f(b+d+f !=0)
- 解题思路
- 分数比化解为整数比
- 需要引入比例系数k,化抽象比例为具体数值计算求解

平均值定理(均值不等式)
- 算术平均数:x1+x2+...+xn/n
- 几何平均数:设n个正数x1...xn称x=n次根号下x1..xn
- 基本定理
- x1...xn为正数时,它们的算术平均值不小于几何平均值,即x1...xn/n>=n次根号下x1...xn,当且仅当x1=...=xn,等号成立
- 若a>0,b>0,则a+b/2>=根号下ab(a+b>=2根号下ab),当且仅当a=b时等号成立(一正二定三相等)
- 积为定值,则求和存在最小值
- 和为定值,则求积存在最大值
- a+1/a>=2(a>0)当且仅当a=1时取最小值2,即对正数而言互为倒数的两个数之和不小于2
- 扩展
- a+b+c>=3*3次根号下abc(a、b、c>0)当且仅当a=b=c时取得等号
- a+b+c+d>=4*4次根号下abcd(a、b、c、d>0)当且仅当a=b=c=d时取得等号

整式与分式(平均1-2题)
因式分解
- 概念:把一个多项式化成几个整式的积的形式,本质就是化和为积,例如x^2 + 3x +2 = (x+2)(x+1)
- 注意:因式分解必须在指定的范围内分解到不能再分解为止
- 常用方法
- 分组分解法:例如am+bm+an+bn=(a+b)(m+n)
- 平方差公式:a^2-b^2=(a-b)(a+b)
- 完全平方公式:(a+_b)^2=a^2+-2ab+b^2
- 立方和与立方差公式:a^3+-b^3=(a+-b)(a^2-+ab+b^2)
- 三项完全平方和公式:(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc
- 完全立方和公式:(a+b)^3=a^3+3a^2b+3ab^2+b^3
- 拓展公式:(a-b)^2+(b-c)^2+(a-c)^2=2[a^2+b^2+c^2-ab-ac-bc]
- 十字相乘法:如x^2+5x+6=(x+2)(x+3)
因式定理
- 出题模式
- 代数式能被某个式子整除
- 某个式子是代数式的因式
- 代数式含有某某因式
- 解题模式
- 令因式为零,求得x的值
- 因式为根,根带入原式,代数式为零



代数式化简
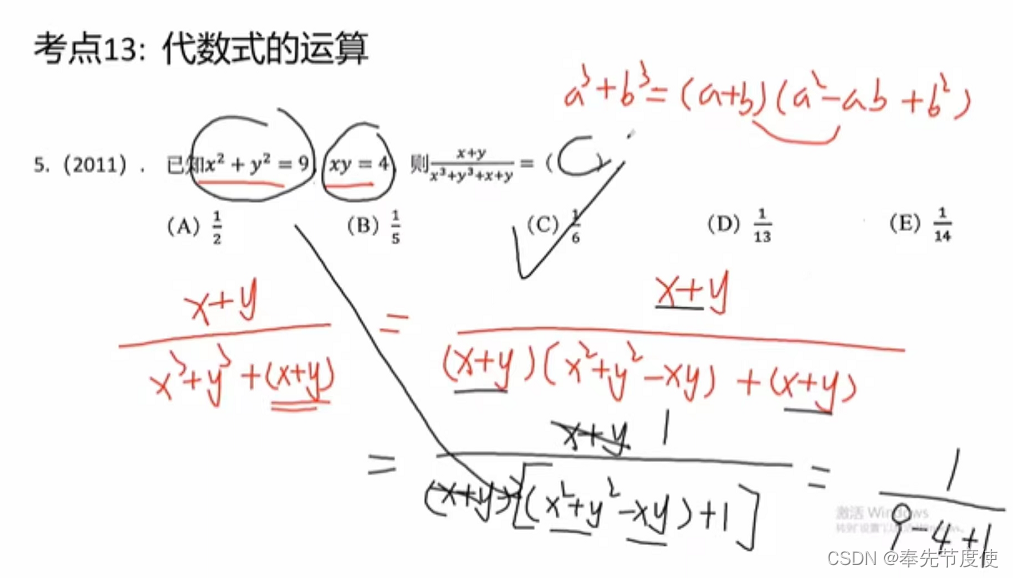

裂项相消法(数列求和或分式化简)
- 概念:实质就是因式分解的一种形式变换,以若干个分式相加,每个分式的分子都是1,然后重新组合,使之能消去一些项,最终达到求和目的
- 1/n(n+k)=1/k(1/n-1/(n+k)),即1/(大)(小)=1/大-小(1/小-1/大)

集合与函数(平均1-2题)
集合
- 性质
- 确定性:元素在一个集合或不在一个集合,不能模糊
- 相异性:集合中的元素不能重复
- 无序性:集合中的元素没有顺序要求
- 集合中运算包括并、交、补大部分使用文氏图表示

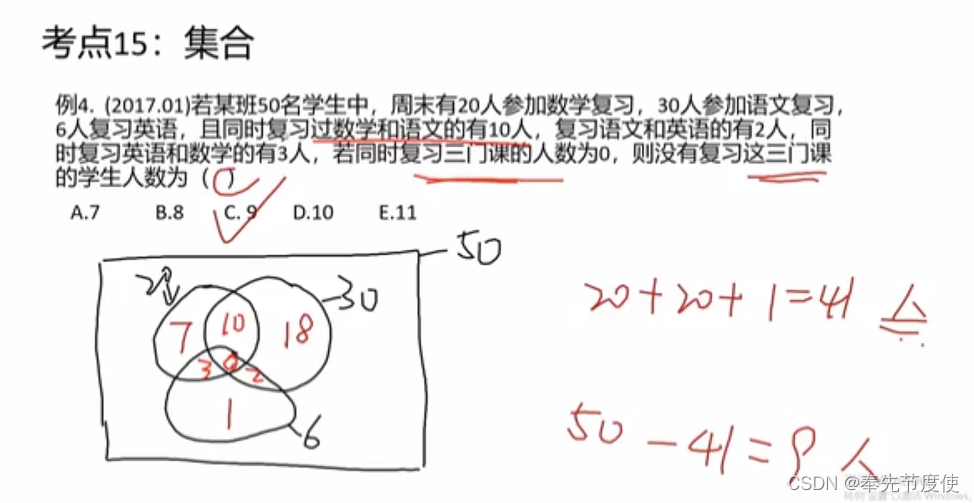
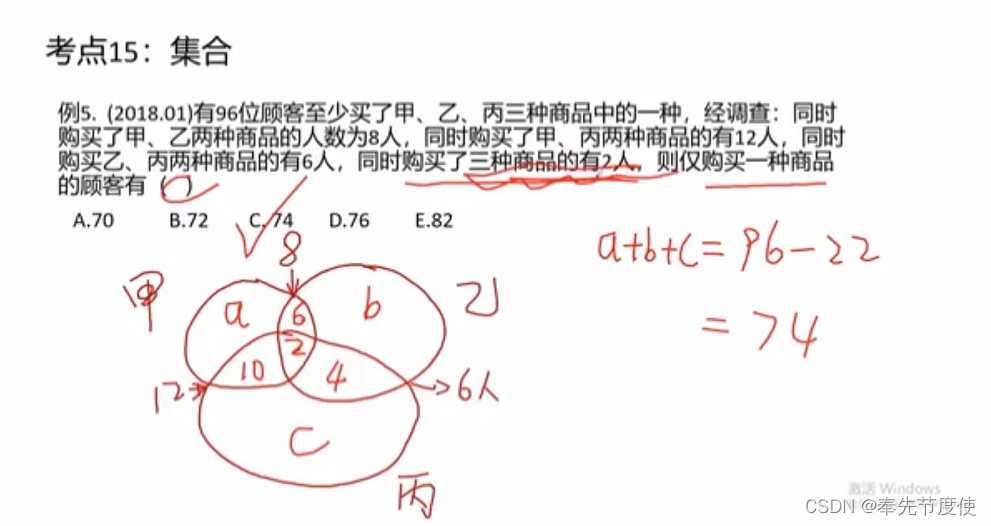
一元一次函数
- 定义:一般在某一变化过程中有两个变量x和y,如果给定一个x,相应确定一个y值,那么称y是x的函数,x是自变量,y是因变量
- 若两个变量x,y关系可以表示为y=kx+b(k、b为常数,k!=0),则称y是x的一次函数,当b=0时则y=kx(k!=0)称y是x的正比例函数。注意:一次函数都是一条直线

一元二次函数
- 基本定义
- y=ax^2+bx+c(a!=0,a、b、c是常数),对称轴x=-b/2a,顶点坐标(-b/2a,4ac-b^2/4a),最值在顶点处取得(a>0为最小值,a<0表示函数有最大值)
- 表达式
- 一般式:y=ax^2+bx+c
- 顶点式:y=a(x+b/2a)^2+4ac-b2/4a
- 两根式:y=a(x-x1)(x-x2)
- x1,x2表示函数与x轴交点的横坐标/函数的零点/对应一元二次方程的两个根
- 一元二次函数性质
- a决定抛物线的开口方向,a>0向上,a<0向下
- 对称轴-b/2a>0表示在y轴右侧,<0表示y轴左侧,=0表示对称轴就是y轴
- c>0表示抛物线与y轴的交点在原点上方,=0表示过原点,<0表示在原点下方
- 判别式吧b^2-4ac决定抛物线与x轴的交点个数,>0表示有两个,=0有一个且顶点在x轴上,<0表示无交点
- 若a+b+c=0,则抛物线过点(1,0);若a-b+c=0,则抛物线过点(-1,0)



指数函数与对数函数
- 指数函数
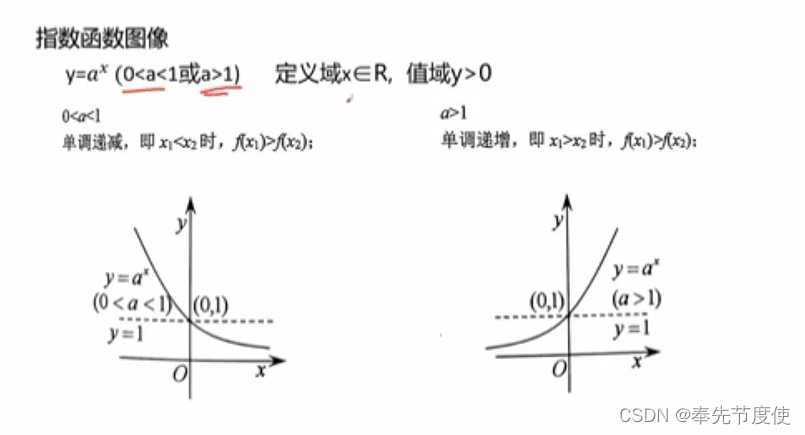
- 定义:y=a^x(a>0且a!=1)称为指数函数,x为自变量
- 运算法则
- a^m * a^n = a^m+n
- a^m / a^n = a^m-n
- (a^m)^n = a^mn
- (ab)^m = a^m*b^m
- a^0 = 1;a^-p = 1/a^p(a!=0)

- 对数函数
- 定义:y=logaX(a>0且a!=1,x>0),a为底数,x为真数,y是以a为底x的对数
- 与指数互为反函数:a^m = b 《=》m=logab
- 运算法则
- logaMN=logaM+logaN
- logaM/N=logaM-logaN
- logaM^n=nlogaM
- loga^Nb^M=M/Nlogab
- 换底公式
- logaN=logbN/logba
- loga1=0;logaa=1;lg2+lg5=1;
- 定义:y=logaX(a>0且a!=1,x>0),a为底数,x为真数,y是以a为底x的对数


方程与不等式(平均2-4题)
方程与根的判别式
- 一元一次方程:只含有一个未知数,并且未知数的最高次数为1,其中方程ax+b=0(x为未知数,a!=0)为标准一元一次方程形式,方程的解为x=-b/a;
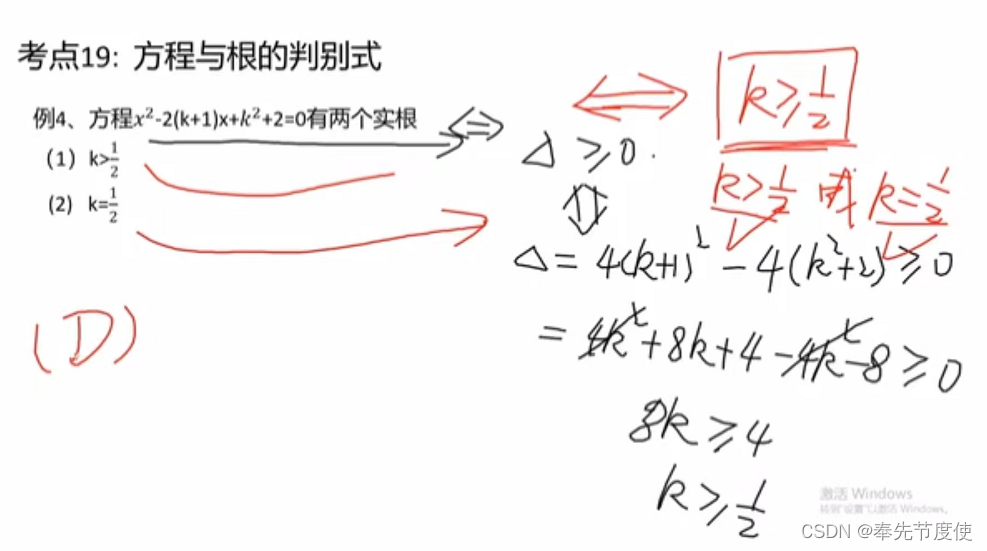
- 一元二次方程:ax^2+bx+c=0(a!=0),a是二次项系数,b是一次项系数,c是常数项
- 根的判别式b^2-4ac
- >0时,方程有两个不等实根,根x=-b+-根号下b^2-4ac/2a
- =0时,存在两个相等实根,x=-b/2a
- <0时,方程无实根
- b^2-4ac联考中自然语言表达
- b^2-4ac=0
- 方程有两个相等实根/重实根
- 函数抛物线与x轴有且仅有一个交点/零点
- 抛物线与x轴相切
- 函数是一个完全平方公式
- 函数抛物线的最大/小值为0
- 仅存在一个x使得ax^2+bx+c=0成立
- b^2-4ac>0
- 方程有两个不相等的实数根
- 抛物线与x轴相交/有两个交点
- 函数或方程有两个零点
- 直线与抛物线有两个交点
- b^2-4ac<0
- 方程没有实数根
- 函数抛物线与x轴没有交点/零点
- 抛物线与x轴相离
- 直线与抛物线无交点
- 二次函数图像恒位于x轴上方/下方
- b^2-4ac>=0
- 方程有两个实数根
- 方程有两个正根
- 方程有两个负根
- 方程有根
- b^2-4ac=0
- 根的判别式b^2-4ac
- 是否对二次项系数a=0进行讨论
- 如果题目中明确二次函 数、一元二次方程、一元二次不等式、抛物线等则默认a!=0
- 若题目知识表示是函数、方程、不等式,则需要对a是否为0进行分类讨论
韦达定理
- 定义:ax^2+bx+c=0(a!=0)的两个根为x1,x2,则
- x1+x2=-b/a
- x1*x2=c/a
- 扩展公式
- x1^2+x2^2=(x1+x2)^2-2x1x2
- x1^3+x2^3=(x1+x2)[(x1+x2)^2-3x1x2]
- |x1-x2|=根号下b^2-4ac/|a|
- |x1-x2|不同自然语言表达形式
- 方程两根之差的绝对值
- 方程两根之间的距离
- 函数抛物线截得x轴的长度
- 函数抛物线与两坐标轴围成的三角形的底边长
- |x1-x2|不同自然语言表达形式

方程根的分布
- 根的分布是个综合问题,需要同时使用判别式和韦达定理
- 一元次方程ax^2+bx+c=0(a!=0)有两个正根
- b^2-4ac>=0
- x1+x2=-b/a>0
- x1x2=c/a>0
- 一元次方程ax^2+bx+c=0(a!=0)有两个负根
- b^2-4ac>=0
- x1+x2=-b/a<0
- x1x2=c/a>0
- 一元次方程ax^2+bx+c=0(a!=0)有一个负根,一个正根
- b^2-4ac>0
- x1x2=c/a<0
- 一元次方程ax^2+bx+c=0(a!=0)有两个根x1,x2且满足m<x1<n,p<x2<q

- f(m)f(n)<0
- f(p)f(q)<0
- 一元次方程ax^2+bx+c=0(a!=0)有两个根x1,x2且一根大于k,一根小于k
- 则无论a>0还是a<0都有af(k)<0
- 一元次方程ax^2+bx+c=0(a!=0)有两个正根
分式方程
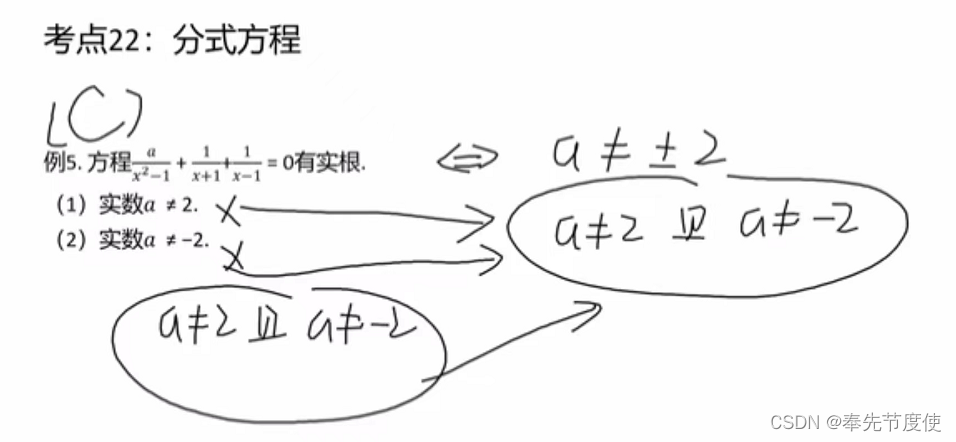
- 思路就是将分式方程转换成整式方程
- 特殊解法:换元法(整体思维),还需要考虑是否存在增根等
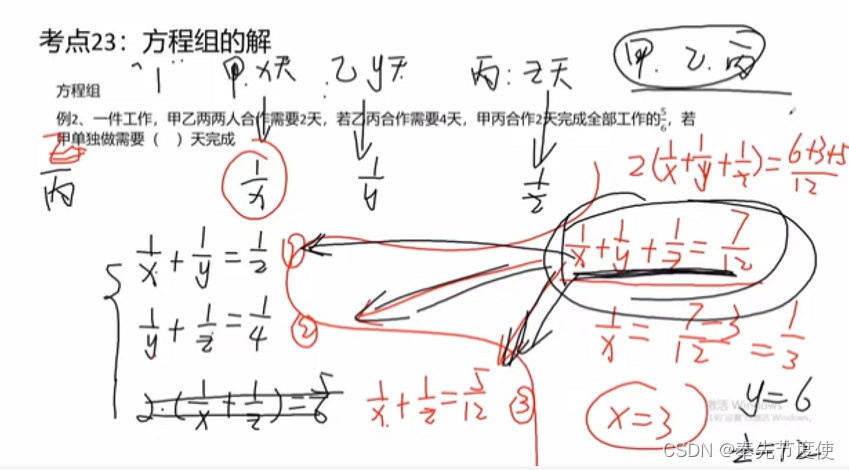
方程组的解
不等式的性质
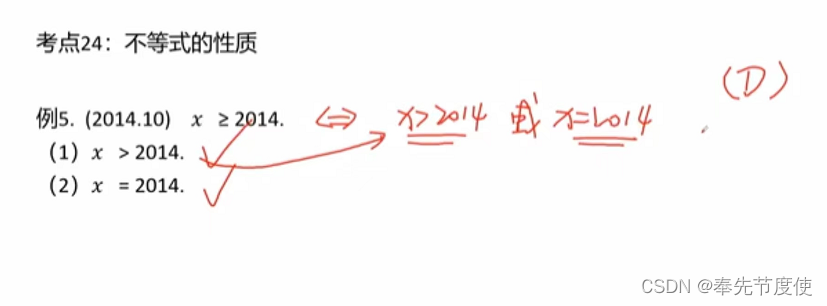
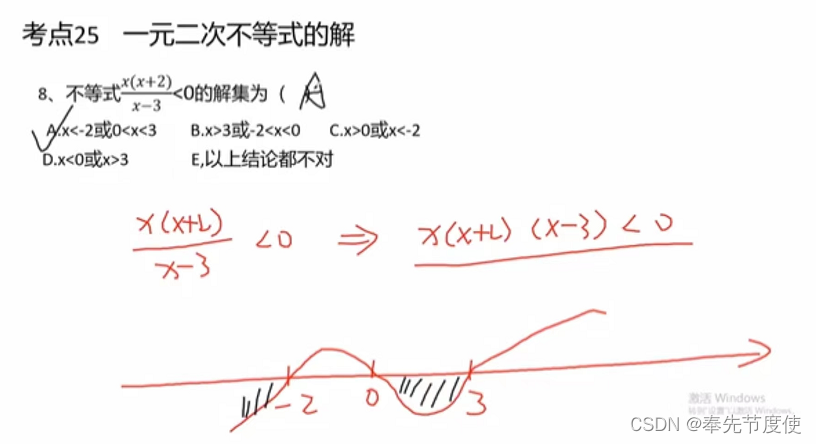
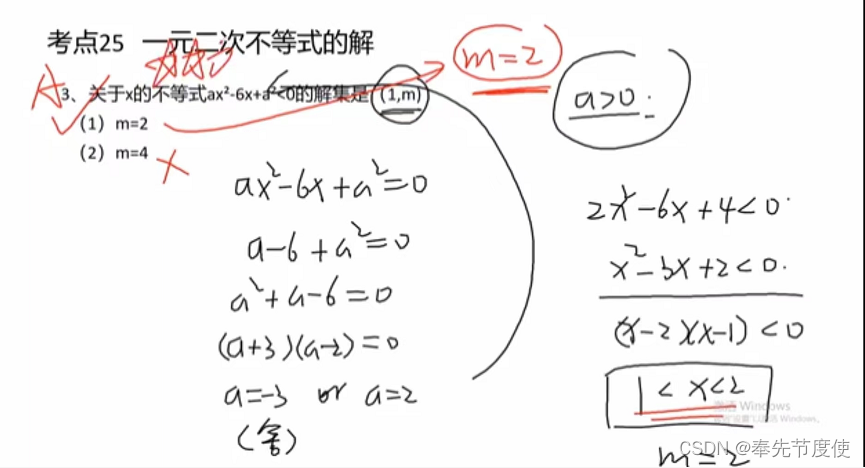
一元二次不等式的解
- 基本概念:不等式中含有一个未知数,未知数的次数为2,且不等式两边都是整式
- 解题思路:不等式看做方程式,然后结合抛物线法(数形结合思想)
- 一元二次不等式的解法

- 不等式解集的边界即为方程的根/零点/与x轴的交点

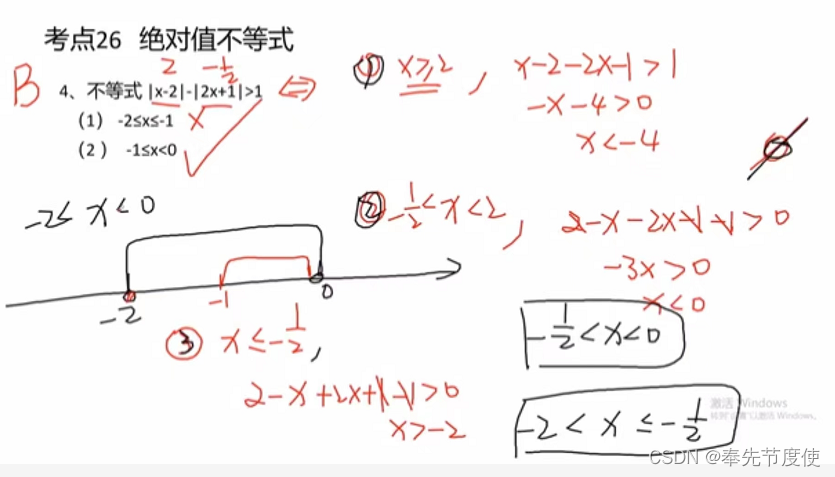
绝对值不等式(难点)
- 解题思路:解含有绝对值不等式的关键是去掉式子中的绝对值符号,常用方法如下
- 平方法:需要确保两边均为非负性才能平方
- 定义法分类讨论
- |f(x)|>f(x),如|x/x-1|>x/x-1
- f(x)>=0时|f(x)|=f(x)
- f(x)<0时|f(x)|=-f(x)
- |f(x)|<g(x)时需要注意g(x)自带定义域
- |f(x)|>f(x),如|x/x-1|>x/x-1
- 公式法
- |f(x)|<a,a>0时则有-a<f(x)<a
- |f(x)|>a,a>0时则有f(x)>a或者f(x)<-a


数列(平均2-3题)
数列相关定义
- 定义:数列是按照一定顺序排列着的一列数
- an与{an}概念不同,an表示数列的第n项,{an}表示数列
- 数列和集合区别
- 集合元素确定、无序、互异
- 数列元素确定、有序、可重复
- an与S(前n项和)关系
- an=S1(n=1)
- an=Sn=Sn-1(n>=2)
等差数列
- 定义:如果一个数列从第二项起,每一项与它前一项的差等于同一个常数
- 该常数为公差d,可正可负,可0,为0时表示常数项
- 通项公式
- an = a1 +(n-1)d
- an = am +(n-m)d 《=》d=an-am / n-m(n!=m)
- 扩展
- 常数列思想:题目中只有单一条件,此时将每个数列项看做常数项
- 等差中项/均值:如a,b,c为等差数列,则2b=a+c
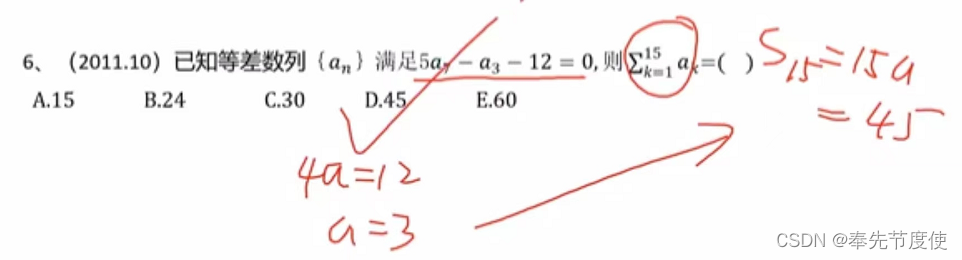
- 等差数列前n项和公式
- sn=n(a1+an)/2 《=》sn=d/2n^2+(a1-d/2)n,即sn是关于n的二次函数(常数项为0)
- 即可推出d>0,Sn有最小值,d<0有最大值
- sn=An^2+Bn+C,若C=0则为等差数列,若C!=0则从第二项开始是等差数列
- sn=n(a1+an)/2 《=》sn=d/2n^2+(a1-d/2)n,即sn是关于n的二次函数(常数项为0)
- 等差数列连续几项之和构成的新数列仍然是等差数列,即Sn,S2n-Sn...
- 等差数列判定法
- 定义法:an-an-1=d,则为等差数列
- 通项公式法:an = Pn+q,则为等差数列
- 中项公式法:2an+1=an + an+2,则为等差数列
- 前n项和公式法:sn=An^2 + Bn,则为等差数列


等比数列
- 定义:如果一个数列从第二项起,每一项与它前一项的比值等于同一个常数
- 该常数为公比q,q!=0,当q=1时表示非0的常数列
- 通项公式
- an = a1 * q^n-1
- an = am * q^n-m
- 等比数列前n项和公式
- q!=1时, Sn=a1(1-q^n)/1-q=(a1-a1q^n)/1-q
- q=1时,Sn=na1
- q!=0且q!=1时,则Sn=A-Aq^n《=》Sn=A+Bq^n(A+B=0)
- 等比数列性质:若m+n=p+k,则am*an=ap*ak,特别的若m+n=2p,则am*an=ap^2
- 等比数列判定法
- 定义法:an+1/an=q,则为等比数列
- 通项公式法:an = cq^n,则为等比数列
- 中项公式法:an+1^2=an*an+2,则为等比数列
- 前n项和公式法:Sn=A-Aq^n,则为等比数列
数列综合