文章目录
- 第三章 数据可视化库matplotlib
- 3.1 matplotlib基本绘图操作
- 3.2 plot的线条和颜色
- 3.3 条形图分析
- 3.4 箱型图分析
- 3.5 直方图分析
- 3.6 散点图分析
- 3.7 图表的美化
- 第四章 数据预测库Sklearn
- 4.1 sklearn预测未来
- 4.2 回归数据的预测
- 4.2.1 回归数据的切分
- 4.2.2 线性回归数据模型
- 4.2.3 回归模型评估方法-MSE
- 4.3 二分类数据的预测
- 4.3.1 二分类数据的切分
- 4.3.2 逻辑回归数据模型
- 4.3.3 二分类模型评估指标-准确率
- 4.3.2 逻辑回归数据模型
- 4.3.3 二分类模型评估指标-准确率
第三章 数据可视化库matplotlib
3.1 matplotlib基本绘图操作
-
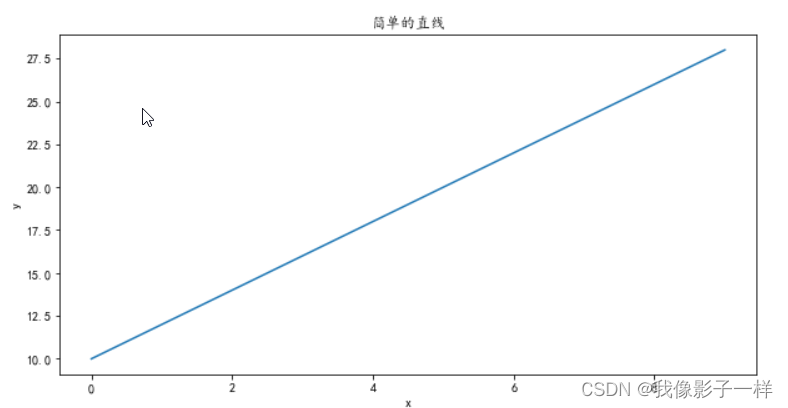
import matplotlib.pyplot as plt import numpy as np # 中文设置 plt.rcParams['font.sans-serif'] =['KaiTi'] # 指定默认字体 plt.rcParams['axes.unicode_minus'] = False #解决保存图像是负号'-'显示为方块的问题 # 设置图形大小,即设置画布 plt.figure(figsize=(10,5)) # 画直线 x = np.arange(10) y = 2 * x + 10 plt.plot(x, y) # 画图 # x,y轴的名称 plt.xlabel('x') plt.ylabel('y') # 标题 plt.title("简单的直线") plt.show() # 展示图形
3.2 plot的线条和颜色
-
线条形状设置
-
字符 线条类型 字符 线条类型 ‘-’ 实线 ‘–’ 虚线 ‘-.’ 虚点线 ‘:’ 点线 ‘.’ 点 ‘,’ 像素点 ‘o’ 圆点 ‘v’ 下三角点 ‘^’ 上三角形 ‘<’ 左三角形 ‘>’ 右三角形 ‘1’ 下三叉点 ‘2’ 上三叉点 ‘3’ 左三叉点 ‘4’ 右三叉点 ‘s’ 正方点 ‘p’ 五角点 ‘*’ 星形点 ‘h’ 六边形点 ‘H’ 六边形点2 ‘+’ +号点 ‘x’ 乘号点 ‘D’ 实习菱形点 ‘d’ 瘦菱形点
-
-
常用颜色缩写
-
字符 颜色 英文全称 ‘b’ 蓝色 blue ‘g’ 绿色 green ‘r’ 红色 reed ‘c’ 青色 cyan ‘m’ 品红 magenta ‘y’ 黄色 yellow ‘k’ 黑色 black ‘w’ 白色 white
-
-
示例:
-
import matplotlib.pyplot as plt import numpy as np x = np.linspace(-10,10) len(x) ## 50 y = np.sin(x) len(y) ## 50 # 设置图形大小,即设置画布 plt.figure(figsize=(10,5)) # plt.plot(x, y,'-.',color='r') # 画图 plt.plot(x, y,'b-.') # 标题 plt.title("正弦函数") # x,y轴的名称 plt.xlabel('x') plt.ylabel('y') plt.show() ## 展示图片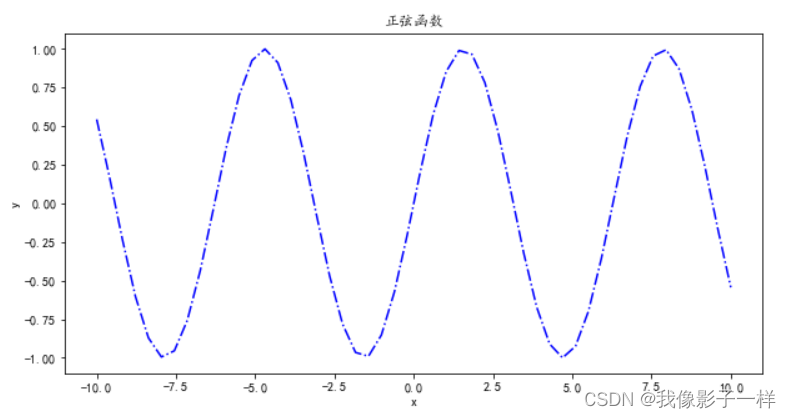
-
3.3 条形图分析
-
示例一:
-
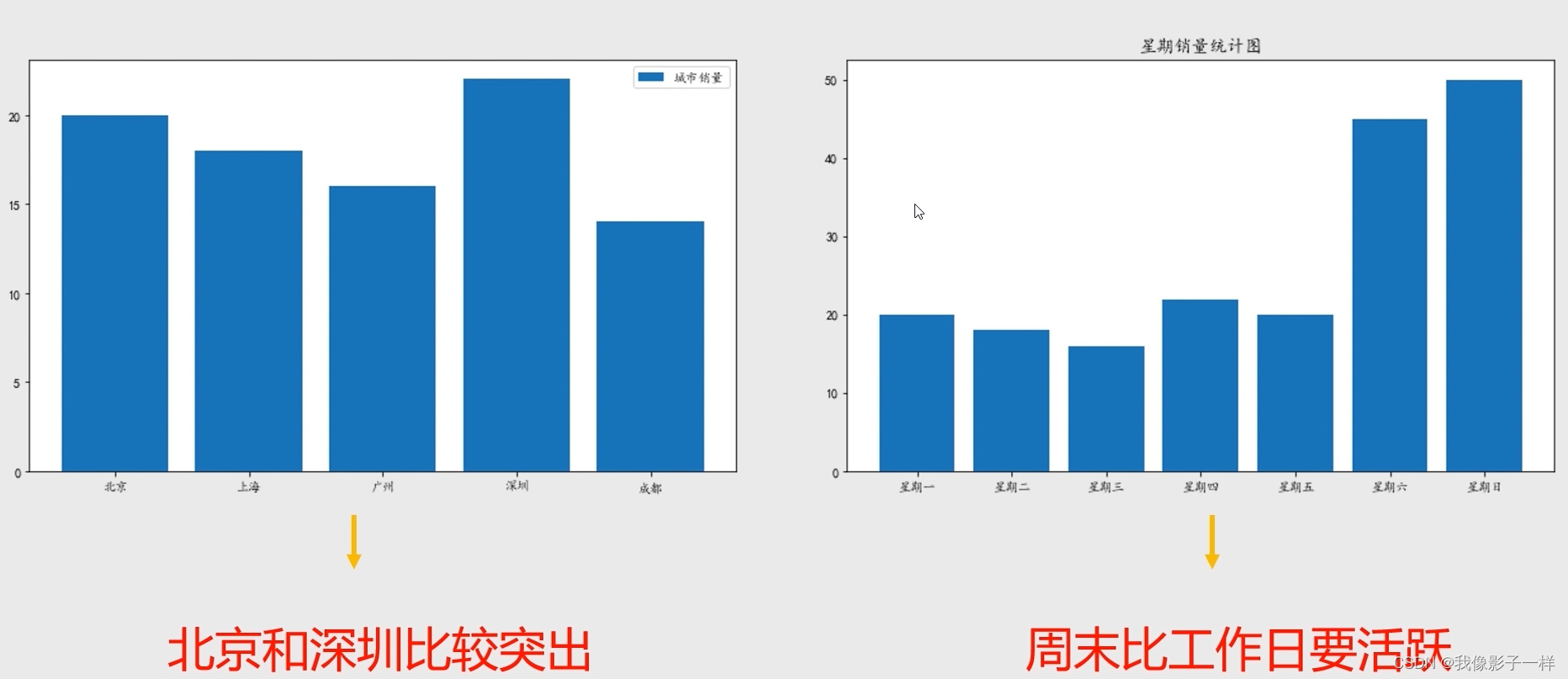
import matplotlib.pyplot as plt import numpy as np # 中文设置 plt.rcParams['font.sans-serif'] = ['KaiTi'] # 设置默认字体 plt.rcParams['axes.unicode_minus'] = False #解决保存图像是负号'-'显示为方块的问题 x = ['北京', '上海', '深圳', '广州'] y = [20, 18, 21, 18] # 设置画布 plt.figure(figsize=(10,6)) # 设置标题 plt.title('各个城市的销量',fontsize=16) ## fontsize设置字体大小 # 画条形图 plt.bar(x, y) plt.show()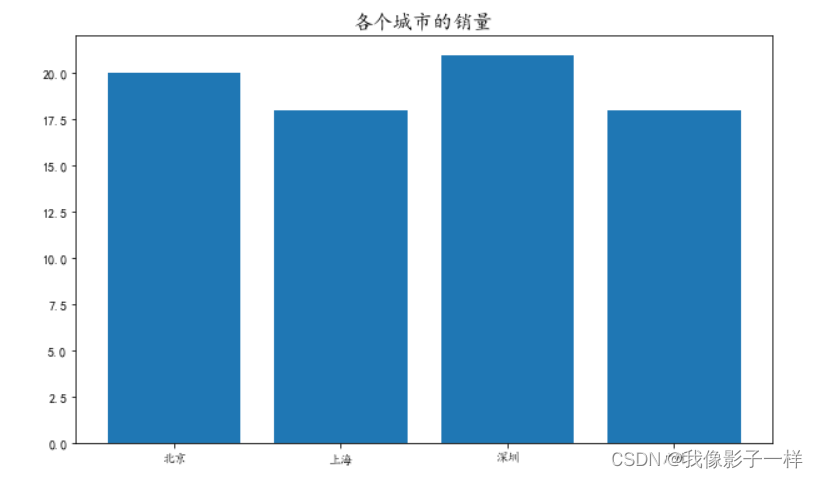
# 设置画布 plt.figure(figsize=(10,6)) # 设置标题 plt.title('各个城市的销量',fontsize=16) ## fontsize设置字体大小 # 画条形图 plt.barh(x, y) plt.show()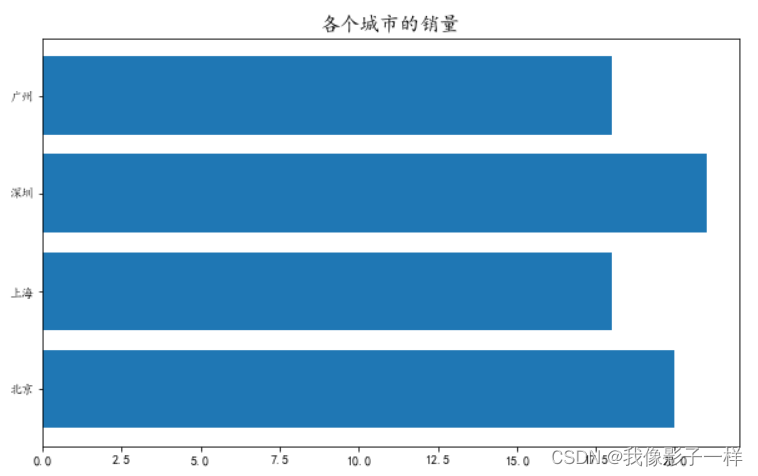
-
-
示例二(数据实操):
-
# 读取data文件夹下面的学生信息表 import pandas as pd data = pd.read_excel("data/学生信息.xlsx") data ## 班级 学号 性别 身高 体重 0 1班 1101 男 173 63 1 1班 1102 女 192 73 2 1班 1103 男 186 82 3 1班 1104 女 167 81 4 1班 1105 女 159 64 5 2班 1201 男 188 68 6 2班 1202 女 176 94 7 2班 1203 男 160 53 8 2班 1204 女 162 63 9 2班 1205 女 167 63 10 3班 1301 男 161 68 11 3班 1302 女 175 57 12 3班 1303 男 188 82 13 3班 1304 男 195 70 14 3班 1305 女 187 69 15 1班 2101 男 174 84 16 1班 2102 女 161 61 17 1班 2103 男 157 61 18 1班 2104 女 159 97 19 1班 2105 男 170 81 20 2班 2201 男 193 100 21 2班 2202 女 194 77 22 2班 2203 男 155 91 23 2班 2204 男 175 74 24 2班 2205 女 183 76 25 3班 2301 女 157 78 26 3班 2302 男 171 88 27 3班 2303 女 190 99 28 3班 2304 女 164 81 29 3班 2305 男 187 73 30 4班 2401 女 192 62 31 4班 2402 男 166 82 32 4班 2403 女 158 60 33 4班 2404 女 160 84 34 4班 2405 女 193 54 -
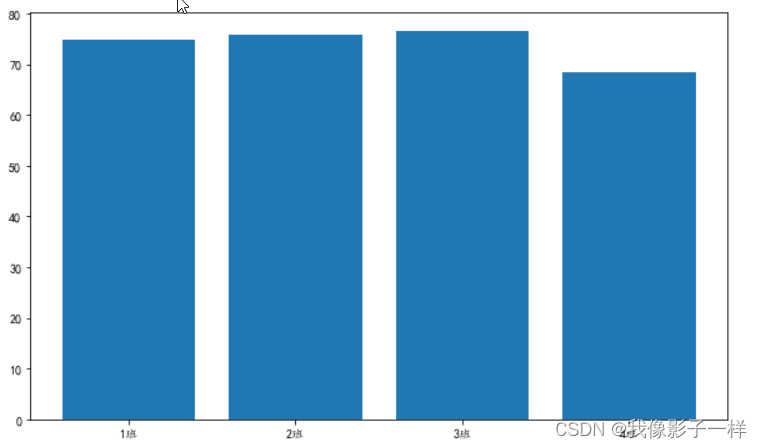
# 查看有多少个班级,分析各个班学生的身高分布(即平均值) data['班级'].unique() ##array(['1班', '2班', '3班', '4班'], dtype=object) a = data.groupby("班级")["身高"].mean().reset_index() a ## 班级 身高 0 1班 169.8 1 2班 175.3 2 3班 177.5 3 4班 173.8 plt.figure(figsize=(10,6)) plt.bar(a["班级"],a["身高"]) plt.show() # 分析各个班级的体重 b = data.groupby("班级")["体重"].mean().reset_index() b ## 班级 体重 0 1班 74.7 1 2班 75.9 2 3班 76.5 3 4班 68.4 plt.figure(figsize=(10,6)) plt.bar(b["班级"],b["体重"]) plt.show()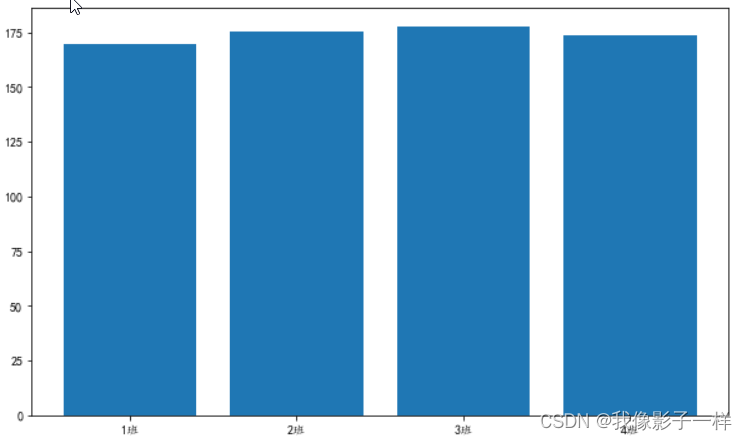
-
3.4 箱型图分析
-
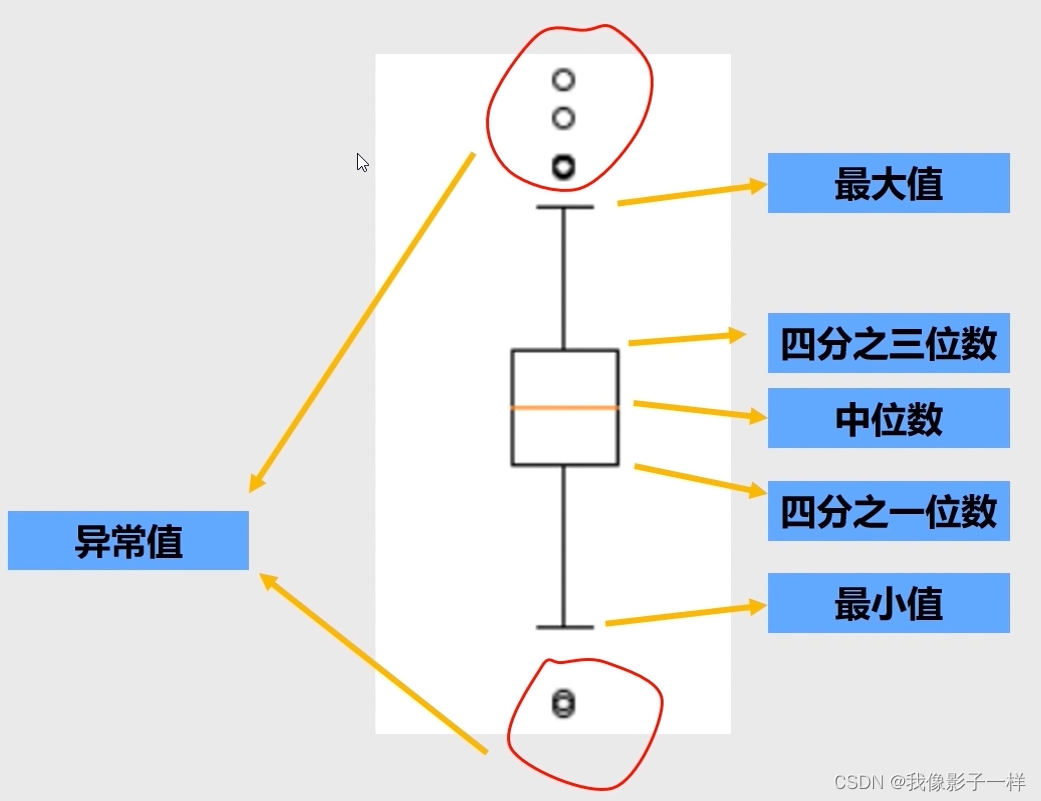
箱型图
- 反映一组数据的分布特征,如:分布是否对称,是否存在异常点;
- 对多维数据的分布可以进行比较;
- 针对连续性变量分析;
-
示例:
-
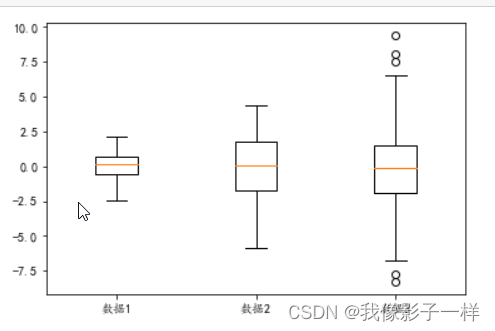
## data文件夹下的箱型图数据.xlsx import matplotlib.pyplot as plt import numpy as np import pandas as pd data = pd.read_excel("data/箱型图数据.xlsx") data ## 数据1 数据2 数据3 0 0.673772 2.877434 2.049346 1 2.094364 1.744089 -2.000739 2 -0.229255 -3.478537 -1.174358 3 0.162415 -0.161255 -0.192022 4 1.601201 0.249620 -3.260043 ... ... ... ... 95 0.802054 -2.125556 4.469550 96 0.704063 -0.020990 -0.325966 97 -1.003454 -0.645414 -3.517653 98 1.009918 1.299786 1.303022 99 0.798712 2.160066 4.128328 100 rows × 3 columns # 单个 plt.boxplot(data["数据1"]) plt.show() # 三个放一起 plt.boxplot([data["数据1"],data["数据2"],data["数据3"]],labels=["数据1", "数据2", "数据3"]) plt.show()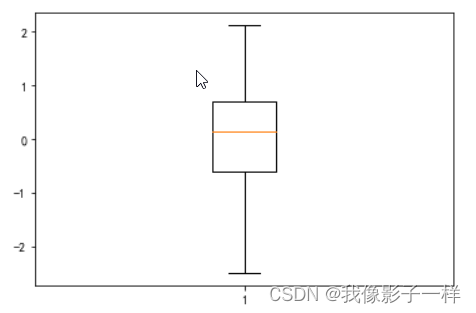
-
3.5 直方图分析
-
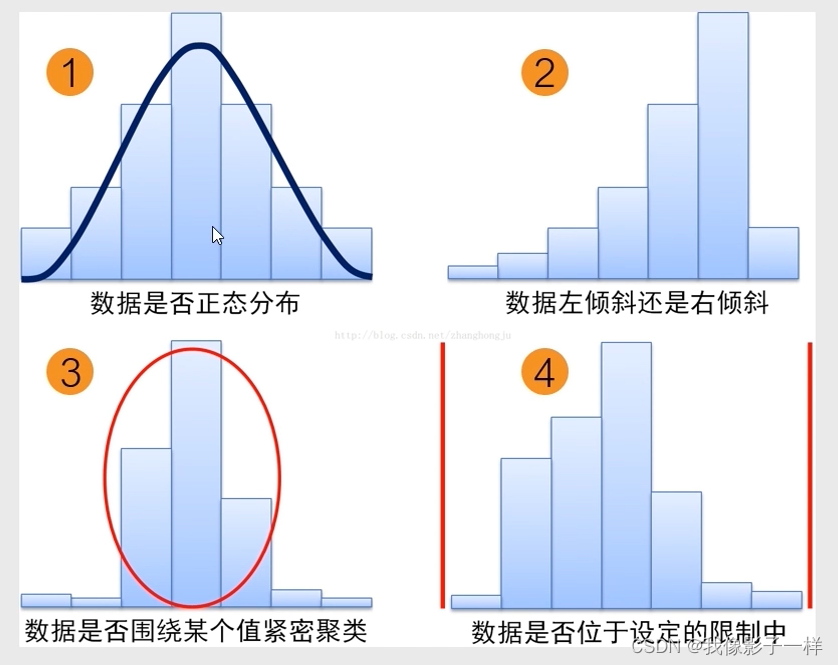
直方图:
-
直方图又称频率分布图,是一种显示数据分布情况的柱形图,即不同数据出现的频率
-
通过这些高度不同的柱形,可以直观、快速地观察数据的分散程度和中心趋势,从而分析流程满足客户的程度
-
-
-
示例(数据实操):
-
# data文件夹下的直方图数据下有两个xlsx文件 import matplotlib.pyplot as plt import pandas as pd data = pd.read_excel("data/直方图数据/乘客信息.xlsx") data ## 乘客编号 年龄 0 1 22 1 2 38 2 3 26 3 4 35 4 5 35 ... ... ... 709 886 39 710 887 27 711 888 19 712 890 26 713 891 32 714 rows × 2 columns data1 = pd.read_excel("data/直方图数据/学生分数.xlsx") data1 ## 学生编号 分数 0 162 56 1 129 28 2 25 2 3 114 21 4 130 29 ... ... ... 185 178 78 186 148 42 187 123 25 188 82 10 189 30 3 190 rows × 2 columns -
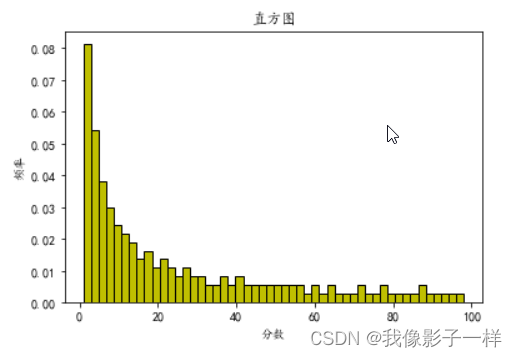
# 分析其年龄分布情况 # 中文设置 plt.rcParams["font.sans-serif"] = ["KaiTi"] # 设置默认字体 plt.rcParams["axes.unicode_minus"] = False # 解决"-"号显示为方块的问题 plt.hist(data["年龄"], bins=20, density=True, color='r', edgecolor='k') # bins表示区间数 # density表示对直方图作出规划(纵轴变为频率了)# edgecolor表示对边缘加颜色 plt.xlabel("年龄") plt.ylabel("频率") plt.title("直方图") plt.show() # 分析班级里面学生成绩的分布情况 plt.hist(data1["分数"], bins=50, density=True,color='y',edgecolor='k') plt.xlabel("分数") plt.ylabel("频率") plt.title("直方图") plt.show()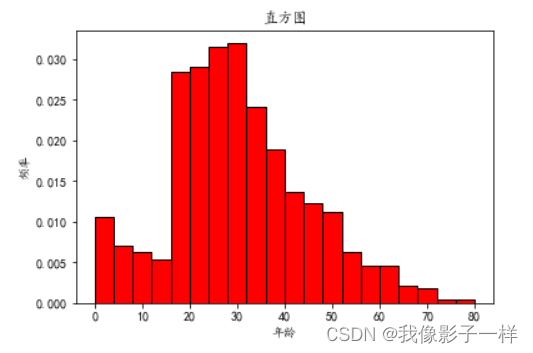
-
3.6 散点图分析
-
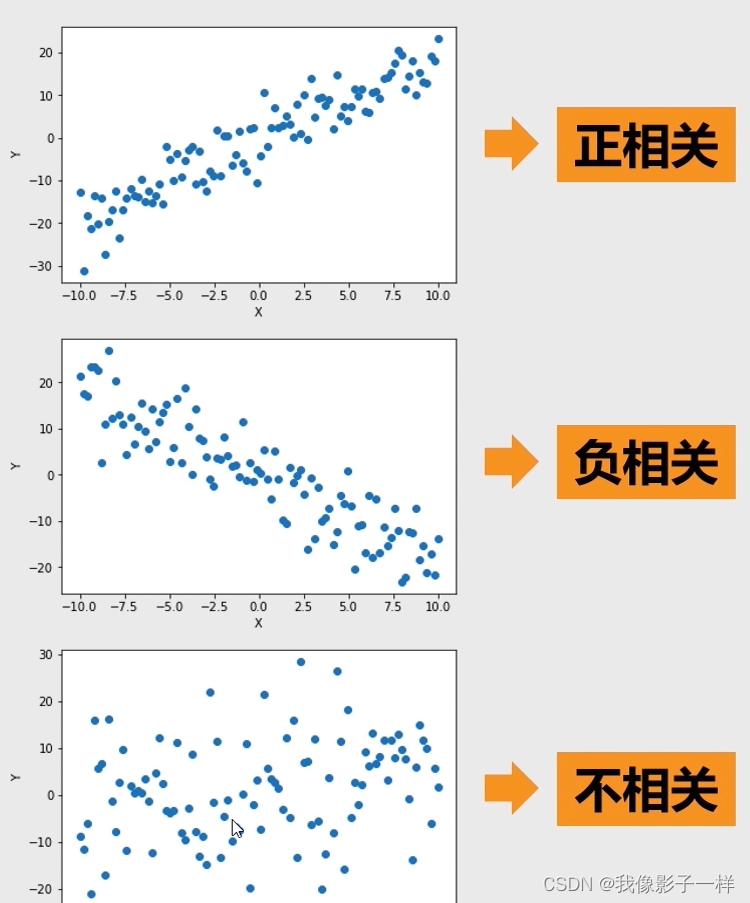
散点图:
- 用两组数据构成多个坐标点,考察坐标点之间的分布,判断两变量之间是否存在某种关联或总结坐标点的分布模式
- 散点图主要用来研究两个连续性变量之间的关系
-
示例(数据实操):
-
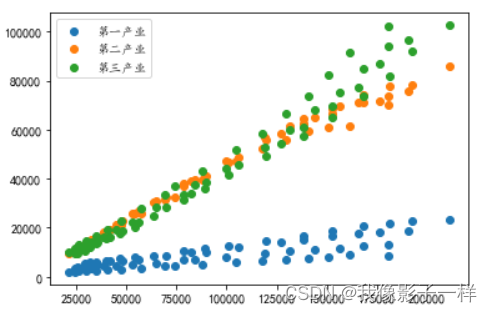
# data文件夹下的国民经济核算季度数据.xlsx import matplotlib.pyplot as plt import pandas as pd data = pd.read_excel("data/国民经济核算季度数据.xlsx") data.columns ## Index(['序号', '时间', '国内生产总值_当季值(亿元)', '第一产业增加值_当季值(亿元)', '第二产业增加值_当季值(亿元)', '第三产业增加值_当季值(亿元)', '农林牧渔业增加值_当季值(亿元)', '工业增加值_当季值(亿元)', '建筑业增加值_当季值(亿元)', '批发和零售业增加值_当季值(亿元)', '交通运输、仓储和邮政业增加值_当季值(亿元)', '住宿和餐饮业增加值_当季值(亿元)', '金融业增加值_当季值(亿元)', '房地产业增加值_当季值(亿元)', '其他行业增加值_当季值(亿元)'], dtype='object') -
# 分析国内生产总值和第一产业的值之间的相关性 # 单个散点图 plt.scatter(data["国内生产总值_当季值(亿元)"],data["第一产业增加值_当季值(亿元)"]) plt.show() # 分析国内生产总值和第一产业的值之间的相关性 # 分析国内生产总值和第二产业的值之间的相关性 # 分析国内生产总值和第三产业的值之间的相关性 # 多个散点图 plt.scatter(data["国内生产总值_当季值(亿元)"],data["第一产业增加值_当季值(亿元)"], label="第一产业") plt.scatter(data["国内生产总值_当季值(亿元)"],data["第二产业增加值_当季值(亿元)"], label="第二产业") plt.scatter(data["国内生产总值_当季值(亿元)"],data["第三产业增加值_当季值(亿元)"], label="第三产业") plt.legend() # legend可以将label调用 plt.show()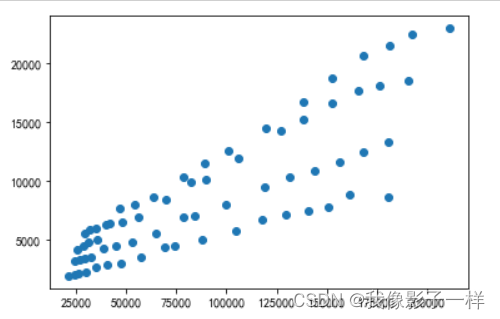
-
3.7 图表的美化
-
基本设置:
-
图例设置 plt.legend(loc=“best”) 画布设置 plt.figure(figsize=(10,6)) 标题设置 plt.title(string,size=10,color=“red”) 横轴设置 plt.xlabel(string,fontsize=10) 纵轴设置 plt.ylabel(string,fontsize=10) 是否显示网络 plt.grid(False) -
loc=“best” 自动找到最佳位置 loc=“upper left” 左上角位置 loc=“upper right” 右上角位置 loc=“lower left” 左下角位置 loc=“lower right” 右下角位置 loc=“center left” 左边中间位置 loc=“center right” 右边中间位置
-
-
示例:
-
import matplotlib.pyplot as plt import numpy as np # 中文设置 plt.rcParams["font.sans-serif"] = ["KaiTi"] # 设置默认字体 plt.rcParams["axes.unicode_minus"] = False # 解决"-"号显示为方块的问题 plt.figure(figsize=(10,6)) # 画布大小 x = np.linspace(0,20,100) plt.plot(x, 2*x, label="曲线1") plt.plot(x, 3*x, label="曲线2") plt.plot(x, 4*x, label="曲线2") plt.legend(loc="best") ## 默认best plt.title("三条曲线",size=16,color="r") plt.xlabel("变量1", fontsize=16,color='c') plt.ylabel("变量2", fontsize=16, color='m') plt.grid(True) plt.show()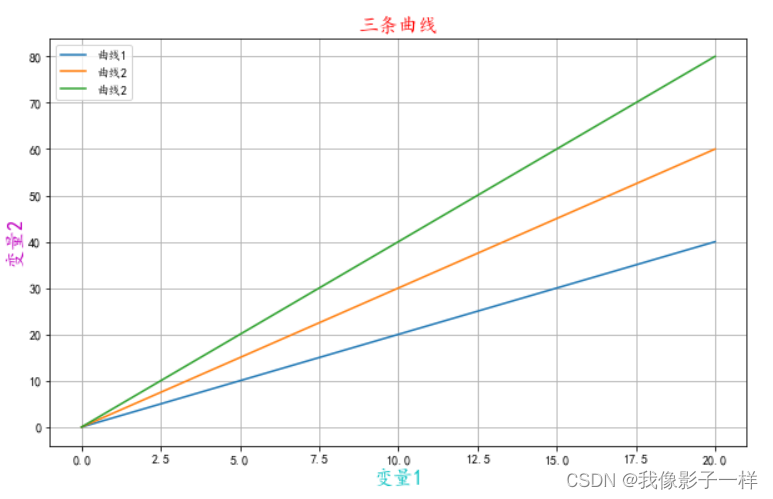
-
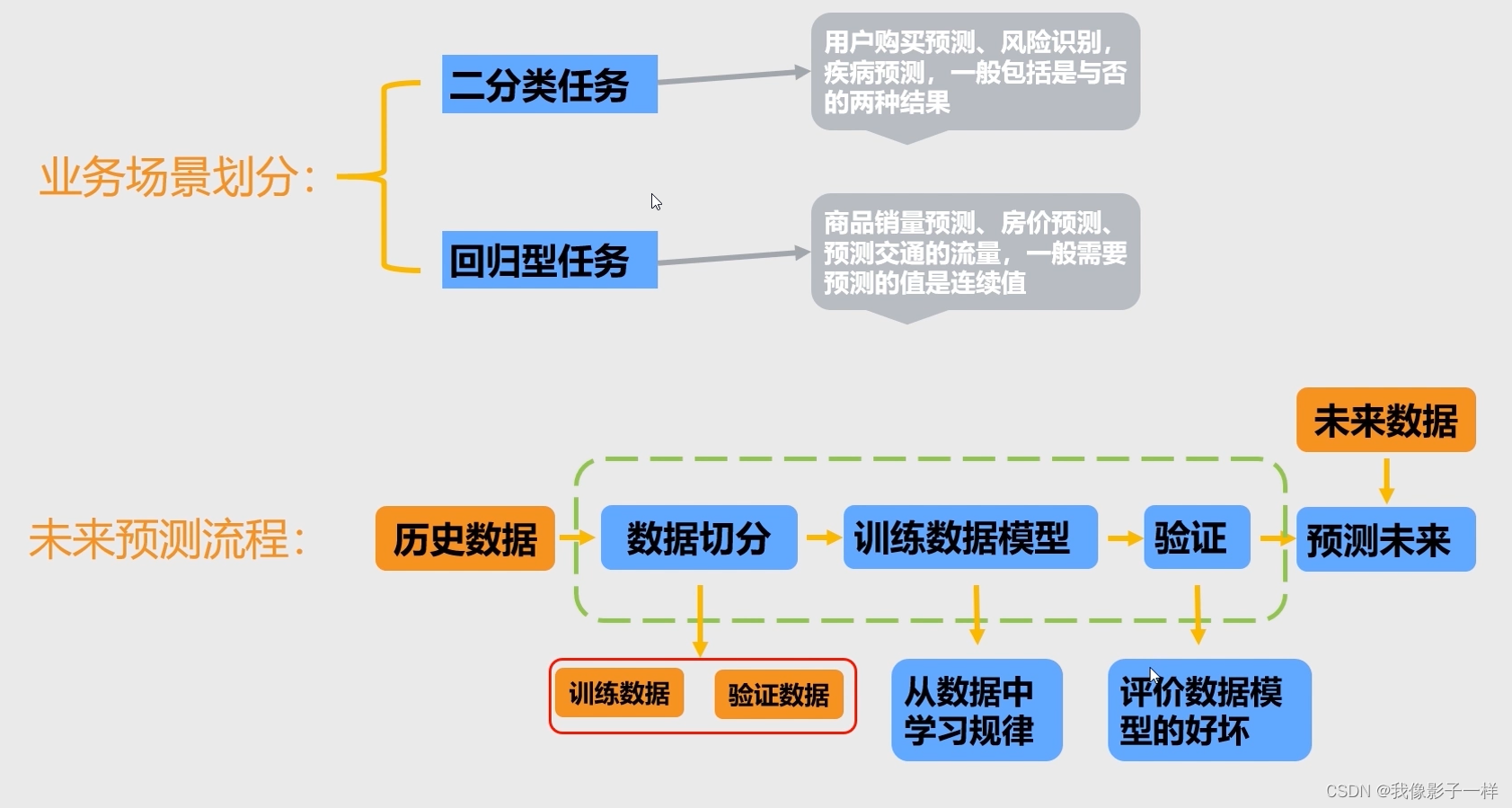
第四章 数据预测库Sklearn
4.1 sklearn预测未来
4.2 回归数据的预测
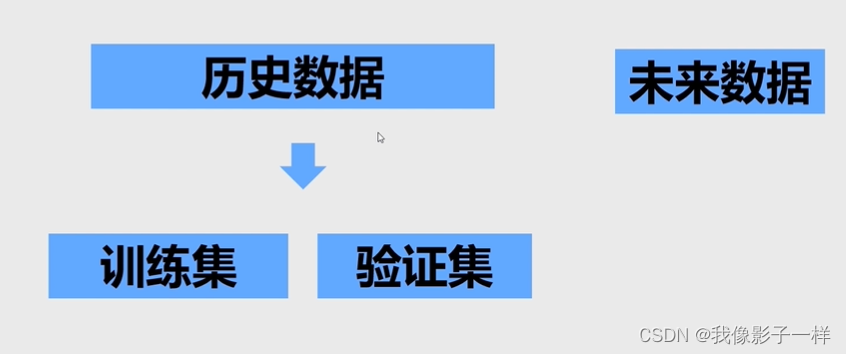
4.2.1 回归数据的切分
-
示例(数据实操):
-
# data文件夹下的房价数据.xlsx import pandas as pd data = pd.read_excel("data/房价数据.xlsx") data ## 城镇人均犯罪率 城镇非零售商用土地比例 一氧化氮浓度 住宅平均房间数 到城市中心区域的加权距离 房价(万元) 0 0.00632 2.31 0.538 6.575 4.0900 2.40 1 0.02731 7.07 0.469 6.421 4.9671 2.16 2 0.02729 7.07 0.469 7.185 4.9671 3.47 3 0.03237 2.18 0.458 6.998 6.0622 3.34 4 0.06905 2.18 0.458 7.147 6.0622 3.62 ... ... ... ... ... ... ... 501 0.06263 11.93 0.573 6.593 2.4786 2.24 502 0.04527 11.93 0.573 6.120 2.2875 2.06 503 0.06076 11.93 0.573 6.976 2.1675 2.39 504 0.10959 11.93 0.573 6.794 2.3889 2.20 505 0.04741 11.93 0.573 6.030 2.5050 1.19 506 rows × 6 columns -
## 用前五个属性来预测房价 from sklearn.model_selection import train_test_split # 训练跟测试切分的方法 train, valid = train_test_split(data, test_size=0.2, shuffle=True, random_state=2020) # 0.8作为训练集,0.2作为验证集,0.2表示把验证集 大小切成0.2 # shuffle=True切分的时候把数据打乱, 便于切出来的数据比较均匀 # random_state 随机种子,返回的是一个列表 # 返回的数据分别是训练集和验证集,分别把他们赋值给train和valid两个变量 data.shape ## 未切分前的形状 ## (506, 6) train.shape ## 切分后的形状 ## (404, 6) valid.shape ## 切分后的形状 ## (102, 6) 404 / 506 # 训练集 ## 0.7984189723320159 102 / 506 # 验证集 ## 0.2015810276679842 -
train ## 城镇人均犯罪率 城镇非零售商用土地比例 一氧化氮浓度 住宅平均房间数 到城市中心区域的加权距离 房价(万元) 215 0.19802 10.59 0.489 6.182 3.9454 2.50 191 0.06911 3.44 0.437 6.739 6.4798 3.05 107 0.13117 8.56 0.520 6.127 2.1224 2.04 442 5.66637 18.10 0.740 6.219 2.0048 1.84 230 0.53700 6.20 0.504 5.981 3.6715 2.43 ... ... ... ... ... ... ... 195 0.01381 0.46 0.422 7.875 5.6484 5.00 118 0.13058 10.01 0.547 5.872 2.4775 2.04 323 0.28392 7.38 0.493 5.708 4.7211 1.85 392 11.57790 18.10 0.700 5.036 1.7700 0.97 352 0.07244 1.69 0.411 5.884 10.7103 1.86 404 rows × 6 columns valid ## 城镇人均犯罪率 城镇非零售商用土地比例 一氧化氮浓度 住宅平均房间数 到城市中心区域的加权距离 房价(万元) 409 14.43830 18.10 0.5970 6.852 1.4655 2.75 247 0.19657 5.86 0.4310 6.226 8.0555 2.05 399 9.91655 18.10 0.6930 5.852 1.5004 0.63 300 0.04417 2.24 0.4000 6.871 7.8278 2.48 321 0.18159 7.38 0.4930 6.376 4.5404 2.31 ... ... ... ... ... ... ... 204 0.02009 2.68 0.4161 8.034 5.1180 5.00 495 0.17899 9.69 0.5850 5.670 2.7986 2.31 244 0.20608 5.86 0.4310 5.593 7.9549 1.76 413 28.65580 18.10 0.5970 5.155 1.5894 1.63 216 0.04560 13.89 0.5500 5.888 3.1121 2.33 102 rows × 6 columns
-
4.2.2 线性回归数据模型
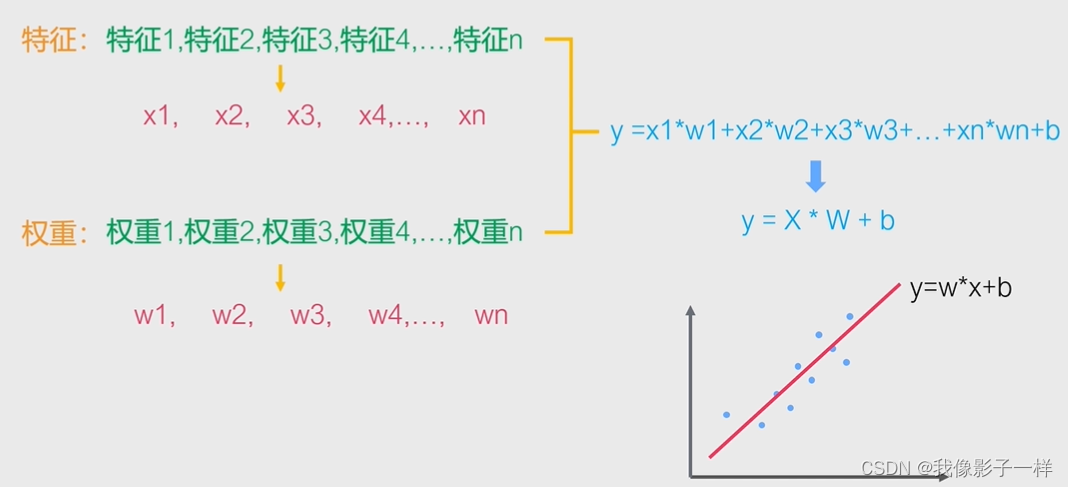
-
示例(实操接4.2.1数据):
-
# 预测房价 # 导入线性回归模型 from sklearn.linear_model import LinearRegression model = LinearRegression() # 定义一个数据模型 # train , valid # 训练集训练数据,验证集用来预测数据 model.fit(train[['城镇人均犯罪率', '城镇非零售商用土地比例','一氧化氮浓度','住宅平均房间数','到城市中心区域的加权距离']], train['房价(万元)']) # fit传入需要训练的特征,这里需要传入除预测外的所有属性 ,fit表示训练的意思 ## LinearRegression() pred = model.predict(valid[['城镇人均犯罪率', '城镇非零售商用土地比例','一氧化氮浓度','住宅平均房间数','到城市中心区域的加权距离']]) pred # predict表示预测,对验证集的每条数据进行预测 ## array([ 2.46474589, 2.2128151 , 1.65888896, 2.85265327, 2.52879848, 2.2258853 , 2.57939134, 2.59693129, 1.82202357, 2.40885497, 2.77841379, 1.64989292, 2.25647387, 3.30694586, 1.94037339, 2.49620692, 2.03597603, 2.61239847, 1.95491352, 1.73957756, 2.1573622 , 2.82385479, 2.09397049, 2.33096025, 0.80547778, 0.83617233, 2.43902438, 1.73929665, 3.29007521, 0.96528621, 2.80937346, 2.75473389, -0.04440117, 2.4362086 , 2.053418 , 0.87830185, 2.00948295, 2.45519188, 1.94278751, 2.27900789, 2.80594378, 2.2755299 , 2.15347854, 3.23576954, 1.9600308 , 2.26173723, 2.29422412, 2.06932986, 2.27333606, 2.95266904, 2.84799092, 2.59296111, 2.65458646, 1.42464319, 1.82023523, 1.16141491, 2.70465962, 2.31695954, 1.55678262, 2.46458798, 2.43287322, 2.23338117, 2.67973044, 4.33672353, 2.95615622, 2.53254281, 2.70089423, 0.27060842, 1.71579957, 2.12512989, 2.5633941 , 2.31433153, 2.84858425, 2.03601581, 2.46245774, 2.02078349, 2.25731773, 2.38199773, 2.14867614, 2.46881375, 2.32091925, 2.16436359, 3.11908093, 3.43351395, 3.3118866 , 1.69532309, 1.87010176, 2.3609788 , 3.13228058, 2.08536776, 1.75231547, 1.93768106, 2.04788031, 2.28601279, 2.1095751 , 2.38820313, 1.59125697, 3.93697614, 1.97308141, 1.75644051, 0.92296715, 2.05833759]) len(pred) ## 102 train.columns ## Index(['城镇人均犯罪率', '城镇非零售商用土地比例', '一氧化氮浓度', '住宅平均房间数', '到城市中心区域的加权距离', '房价(万元)'], dtype='object') valid.columns ## Index(['城镇人均犯罪率', '城镇非零售商用土地比例', '一氧化氮浓度', '住宅平均房间数', '到城市中心区域的加权距离', '房价(万元)'], dtype='object')
-
4.2.3 回归模型评估方法-MSE
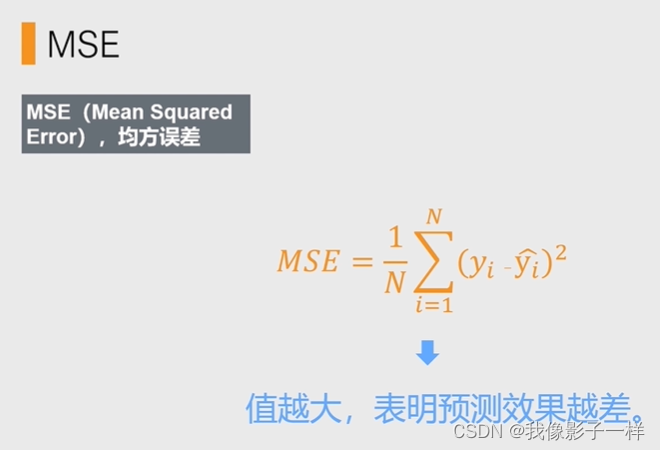
-
MSE
- 即均方误差
- MSE的值越大,表明预测效果越差
-
示例(实操接4.2.2数据):
-
# vaild验证集是真实准确的数据,pred是经过验证集预测的数据 import numpy as np # 导入均方误差 from sklearn.metrics import mean_squared_error # mean_squared_error表示均方误差 mse_error = mean_squared_error(valid['房价(万元)'],pred) # 先传入实际值,再传入预测值 mse_error ## 0.38184398467340286 np.sqrt(mse_error) # 对均方误差进行开方,就可以知道每个样本的偏离程度 # np.sqrt 是numpy的开方 ## 0.6179352592896791
-
4.3 二分类数据的预测
4.3.1 二分类数据的切分
-
示例(数据实操):
-
# data文件夹下的泰坦尼克号数据.xlsx # 0是死亡,1是存活 import pandas as pd data = pd.read_excel("data/泰坦尼克号数据.xlsx") data ## 乘客编号 船票种类 性别 年龄 乘客兄弟姐妹/配偶的个数 乘客父母/孩子的个数 是否存活 0 1 3 male 22.0 1 0 0 1 2 1 female 38.0 1 0 1 2 3 3 female 26.0 0 0 1 3 4 1 female 35.0 1 0 1 4 5 3 male 35.0 0 0 0 ... ... ... ... ... ... ... ... 886 887 2 male 27.0 0 0 0 887 888 1 female 19.0 0 0 1 888 889 3 female -10.0 1 2 0 889 890 1 male 26.0 0 0 1 890 891 3 male 32.0 0 0 0 891 rows × 7 columns data.dtypes # 性别 是字符串类型,不符合字符类型,需要转为数值类型。因为数学模型里面必须要都是数值类型才可以分析 ## 乘客编号 int64 船票种类 int64 性别 object 年龄 float64 乘客兄弟姐妹/配偶的个数 int64 乘客父母/孩子的个数 int64 是否存活 int64 dtype: object data['性别'].value_counts() ## male 577 female 314 Name: 性别, dtype: int64 data['性别'] = data['性别'].apply(lambda x: 0 if x == 'male'else 1) # 用pandas学的apply快速实现转换,然后更新列的数据 data.head() # 显示修改后的前五条数据 ## 乘客编号 船票种类 性别 年龄 乘客兄弟姐妹/配偶的个数 乘客父母/孩子的个数 是否存活 0 1 3 1 22.0 1 0 0 1 2 1 1 38.0 1 0 1 2 3 3 1 26.0 0 0 1 3 4 1 1 35.0 1 0 1 4 5 3 1 35.0 0 0 0 -
from sklearn.model_selection import train_test_split train,valid = train_test_split(data, test_size=0.2, shuffle=True, random_state=2020) data["是否存活"].value_counts() # 0是死亡,1是存活 ## 0 549 1 342 Name: 是否存活, dtype: int64 549 / 342 # 死亡:活着 ##1.605263157894737 train['是否存活'].value_counts() ## 0 444 1 268 Name: 是否存活, dtype: int64 444/268 ## 1.6567164179104477 valid['是否存活'].value_counts() ## 0 105 1 74 Name: 是否存活, dtype: int64 105/74 ## 1.4189189189189189 # 由以上数据可知 训练集是1.6多,而验证集是1.4,跟预测数据1.60的比值差别太大差别太大 ### 解决办法 # 用stratify,进行分层抽样 train,valid = train_test_split(data, test_size=0.2, shuffle=True, random_state=2020, stratify=data["是否存活"]) train['是否存活'].value_counts() ## 0 439 1 273 Name: 是否存活, dtype: int64 439/273 ## 1.6080586080586081 valid['是否存活'].value_counts() ## 0 110 1 69 Name: 是否存活, dtype: int64 110/69 ## 1.5942028985507246
-
4.3.2 逻辑回归数据模型
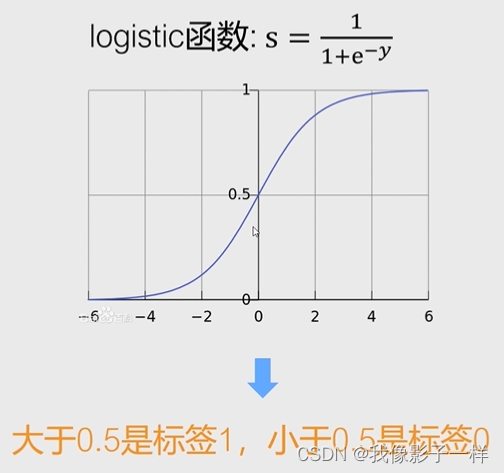
-
logistic函数:
-
# logistic函数曲线 import numpy as np import matplotlib.pyplot as plt x = np.linspace(-10, 10, 100) y = 1 / (1 + np.exp(-x)) # np.exp就是数学中的自然e,np.exp(-x)表示e的-x次方 plt.plot(x, y) plt.show()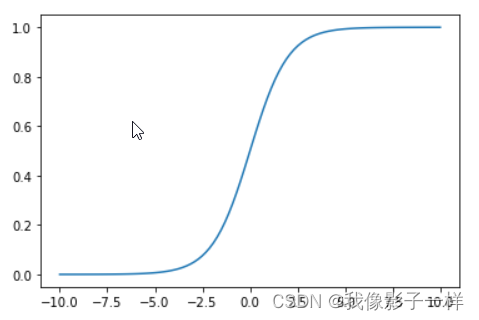
-
-
示例(实操接4.3.1数据):
-
from sklearn.linear_model import LogisticRegression # LogisticRegression 逻辑回归 model = LogisticRegression() # 定义一个数据模型 train.columns # 因为每个乘客的乘客编号都不同,就不熟他们特有的特征了,索引只取其他五个特有的属性 ## Index(['乘客编号', '船票种类', '性别', '年龄', '乘客兄弟姐妹/配偶的个数', '乘客父母/孩子的个数', '是否存活'], dtype='object') # 训练 model.fit(train[['船票种类', '性别', '年龄', '乘客兄弟姐妹/配偶的个数', '乘客父母/孩子的个数']], train['是否存活']) ## LogisticRegression() # 成功 # 预测 pred = model.predict(valid[['船票种类', '性别', '年龄', '乘客兄弟姐妹/配偶的个数', '乘客父母/孩子的个数']]) pred # 预测结果 ## array([0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0], dtype=int64)
-
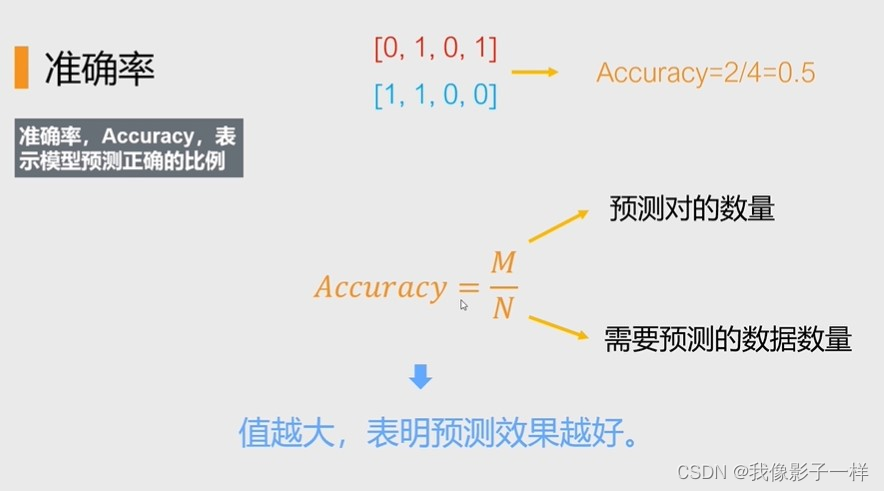
4.3.3 二分类模型评估指标-准确率
-
准确率:
-
准确率,Accuracy,表示模型预测正确地比例
-
A c c u r a c y = M / N Accuracy = M/N Accuracy=M/N
-
M表示预测对的数量,N表示需要预测的数据
-
Accuracy的值越大,表明预测的效果越好
-
-
示例(实操接4.3.2数据):
-
from sklearn.metrics import accuracy_score # accuracy_score 准确率分数,用来计算准确率的 accuracy_score(valid["是否存活"], pred) # 先传入真实数据再传入预测数据 ## 0.776536312849162
-
if x == 'male’else 1)
# 用pandas学的apply快速实现转换,然后更新列的数据
data.head() # 显示修改后的前五条数据
##
乘客编号 船票种类 性别 年龄 乘客兄弟姐妹/配偶的个数 乘客父母/孩子的个数 是否存活
0 1 3 1 22.0 1 0 0
1 2 1 1 38.0 1 0 1
2 3 3 1 26.0 0 0 1
3 4 1 1 35.0 1 0 1
4 5 3 1 35.0 0 0 0
```
-
from sklearn.model_selection import train_test_split train,valid = train_test_split(data, test_size=0.2, shuffle=True, random_state=2020) data["是否存活"].value_counts() # 0是死亡,1是存活 ## 0 549 1 342 Name: 是否存活, dtype: int64 549 / 342 # 死亡:活着 ##1.605263157894737 train['是否存活'].value_counts() ## 0 444 1 268 Name: 是否存活, dtype: int64 444/268 ## 1.6567164179104477 valid['是否存活'].value_counts() ## 0 105 1 74 Name: 是否存活, dtype: int64 105/74 ## 1.4189189189189189 # 由以上数据可知 训练集是1.6多,而验证集是1.4,跟预测数据1.60的比值差别太大差别太大 ### 解决办法 # 用stratify,进行分层抽样 train,valid = train_test_split(data, test_size=0.2, shuffle=True, random_state=2020, stratify=data["是否存活"]) train['是否存活'].value_counts() ## 0 439 1 273 Name: 是否存活, dtype: int64 439/273 ## 1.6080586080586081 valid['是否存活'].value_counts() ## 0 110 1 69 Name: 是否存活, dtype: int64 110/69 ## 1.5942028985507246
4.3.2 逻辑回归数据模型
[外链图片转存中…(img-qmvxTRUZ-1696233196612)]
-
logistic函数:
-
# logistic函数曲线 import numpy as np import matplotlib.pyplot as plt x = np.linspace(-10, 10, 100) y = 1 / (1 + np.exp(-x)) # np.exp就是数学中的自然e,np.exp(-x)表示e的-x次方 plt.plot(x, y) plt.show()[外链图片转存中…(img-eO8xp7LI-1696233196612)]
-
-
示例(实操接4.3.1数据):
-
from sklearn.linear_model import LogisticRegression # LogisticRegression 逻辑回归 model = LogisticRegression() # 定义一个数据模型 train.columns # 因为每个乘客的乘客编号都不同,就不熟他们特有的特征了,索引只取其他五个特有的属性 ## Index(['乘客编号', '船票种类', '性别', '年龄', '乘客兄弟姐妹/配偶的个数', '乘客父母/孩子的个数', '是否存活'], dtype='object') # 训练 model.fit(train[['船票种类', '性别', '年龄', '乘客兄弟姐妹/配偶的个数', '乘客父母/孩子的个数']], train['是否存活']) ## LogisticRegression() # 成功 # 预测 pred = model.predict(valid[['船票种类', '性别', '年龄', '乘客兄弟姐妹/配偶的个数', '乘客父母/孩子的个数']]) pred # 预测结果 ## array([0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0], dtype=int64)
-
4.3.3 二分类模型评估指标-准确率
[外链图片转存中…(img-gQr0jn8Z-1696233196613)]
-
准确率:
-
准确率,Accuracy,表示模型预测正确地比例
-
A c c u r a c y = M / N Accuracy = M/N Accuracy=M/N
-
M表示预测对的数量,N表示需要预测的数据
-
Accuracy的值越大,表明预测的效果越好
-
-
示例(实操接4.3.2数据):
-
from sklearn.metrics import accuracy_score # accuracy_score 准确率分数,用来计算准确率的 accuracy_score(valid["是否存活"], pred) # 先传入真实数据再传入预测数据 ## 0.776536312849162
-