VUE3照本宣科——应用实例API与setup

news2024/11/24 14:43:29

VUE3照本宣科——应用实例API与setup

前言
一、应用实例API
- 1.createApp()
- 2.app.use()
- 3.app.mount()
二、setup

前言

👨‍💻👨‍🌾📝记录学习成果，以便温故而知新

“VUE3照本宣科”是指照着中文官网和菜鸟教程这两个“本”来学习一下VUE3。以前也学过VUE2，当时只再gitee留下一些代码，却没有记录学习的心得体会，有时也免不了会追忆一下。

以后出现“中文官网”不做特殊说明就是指：https://cn.vuejs.org/；菜鸟教程就是指：https://www.runoob.com/vue3/vue3-tutorial.html

一、应用实例API

中文文档中应用实例API 有很多，本文选择前文所述的“zbxk”项目中默认代码中出现的API介绍。

前文讲过“index.html”是前端应用的入口，
在这里插入图片描述首先能看到的是一个ID为app的div，这是SPA渲染的根；然后看到的是引入了src目录下的“main.js”。
接着看main.js，如图：

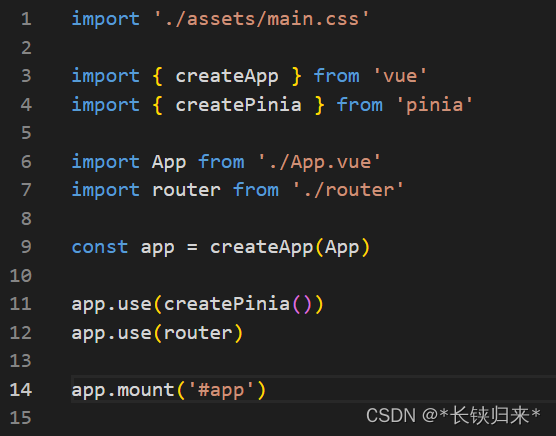
从截图中可以看到createApp() 、app.use() 及app.mount() 3个应用实例API，中文文档实际上有一堆的应用实例API，但是zbxk项目中没有出现，所以不做介绍。有需要深入了解的请参看应用实例 API 。

1.createApp()

功能是创建一个应用实例。

function createApp(rootComponent: Component, rootProps?: object): App
第一个参数是根组件。第二个参数可选，它是要传递给根组件的 props。

项目中的代码：

const app = createApp(App)

是用组件App创建应用app，而组件App是整个项目的父组件

2.app.use()

功能是安装一个插件。

interface App {
use(plugin: Plugin, …options: any[]): this
}
第一个参数应是插件本身，可选的第二个参数是要传递给插件的选项。
插件可以是一个带 install() 方法的对象，亦或直接是一个将被用作 install() 方法的函数。插件选项 (app.use() 的第二个参数) 将会传递给插件的 install() 方法。
若 app.use() 对同一个插件多次调用，该插件只会被安装一次。

项目中的代码：

app.use(createPinia())
app.use(router)

安装了2个插件，分别是状态管理器与路由。

3.app.mount()

功能是将应用实例挂载在一个容器元素中。

参数可以是一个实际的 DOM 元素或一个 CSS 选择器 (使用第一个匹配到的元素)。返回根组件的实例。
如果该组件有模板或定义了渲染函数，它将替换容器内所有现存的 DOM 节点。否则在运行时编译器可用的情况下，容器元素的 innerHTML 将被用作模板。
对于每个应用实例，mount() 仅能调用一次。

项目中的代码：

app.mount('#app')

是把新建的实例app挂载到ID为app的div上。有时也会说成渲染到ID为app的div上，所表达的是一个意思。

二、setup

setup() 钩子是在组件中使用组合式 API 的入口，通常只在以下情况下使用：

1.需要在非单文件组件中使用组合式 API 时。
2.需要在基于选项式 API 的组件中集成基于组合式 API 的代码时。

对于结合单文件组件使用的组合式 API，推荐通过 <script setup> 以获得更加简洁及符合人体工程学的语法。

所以本系列如果不做特别说明，都是尽量使用<script setup>

在src/view目录下AboutView.vue文件添加如下代码：

<script>
export default {
  setup(props, context) {
    // 透传 Attributes（非响应式的对象，等价于 $attrs）
    console.log(context.attrs)

    // 插槽（非响应式的对象，等价于 $slots）
    console.log(context.slots)

    // 触发事件（函数，等价于 $emit）
    console.log(context.emit)

    // 暴露公共属性（函数）
    console.log(context.expose)
  }
}
</script>