---

前言

---

提示：他不是不想多明白些，但是每每在该用脑子的时候，他用了感情。 --老舍《黑白李》

与位运算和数学有关的题目真的不少，很多都是有一定技巧的，好在这些技巧都是相对固定的，我们要做好积累。

1. 位移的妙用

位移操作是一个很重要的问题，可以统计数字中1的个数，在很多高性能的软件中也是大量运用，我们先来看看下面这几道高频题目。

1.1 位1的个数

参考题目介绍：191. 位1的个数 - 力扣（LeetCode）

拓展一下：16进制时怎么统计0的个数

首先我们可以根据题目的要求直接计算，题目给定的n是32位二进制表示下的一个整数，计算位1的个数最简单的方式就是遍历一边n的二进制表示的每一位，判断每一位是否为1，同时还要进行统计。

那问题就是变成了，如何通过位运算来识别到1：举个栗子🌰

[0000 1001 0010 0001 0001 0001 1100 1101]

首先我们需要注意到识别最低为的1，可以这么做

  [0000 1001 0010 0001 0001 0001 1100 1101]
& [0000 0000 0000 0000 0000 0000 0000 0001]
= [0000 0000 0000 0000 0000 0000 0000 0001]

也就是说将原始数字和1进行&运算就能够知道最低位是不是1了，那么其他位置怎么处理呢？

这里有两种思路

• 让1不断地左移
• 将原始数据不断的右移

例如将原始数据右移就是

  [0000 0100 1001 0000 1000 1000 1110 0110]
& [0000 0000 0000 0000 0000 0000 0000 0001]
= [0000 0000 0000 0000 0000 0000 0000 0000]

很明显的就可以判断出第二位是0，然后继续将原始数据右移可以依次判断出每个位置是不是1了。所以这里可以总结下（n >> i) & 1就可以了，所以代码写起来也简单了：

/**
         * 方法1：n整体循环移位
         *
         * @param n
         * @return
         */
    public static int hammingWeight1(int n) {
        int count = 0;
        for(int i = 0; i < 32; i++){
            count += (n >> i) & 1;
        }
        return count;
    }

这个题目也可以通过左移1来实现的，该问题可以留作作业。你可以试着改下代码。

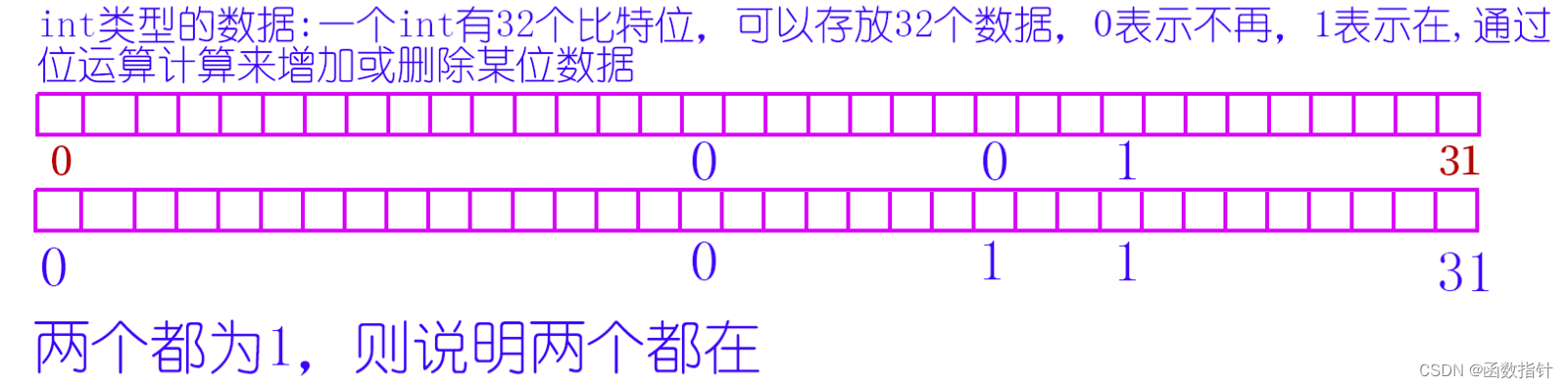
上面的代码写出来，这个问题问题就基本上及格了，但是不是最经典的解法，我们进一步分析，按位与运算的一个性质，对于整数n，计算n&(n - 1)的结果是将n的二进制表示最后一个1变成0。利用这个性质。令n = n &（n - 1），则n的二进制数中的1的个数减少一个，重复该操作，知道n的二进制位中的全部位数变成0，则该操作的次数即时n的位上1的个数。什么意思呢？我们看下图解：

n    			[0000 0100 1001 0000 1000 1000 1110 0110]
n-1  			[0000 0100 1001 0000 1000 1000 1110 0101]
n& (n - 1) =    [0000 0100 1001 0000 1000 1000 1110 0100]

可以看到此时n&(n - 1)的结果是比n少了一个1，此时我们令n = n &(n - 1)，继续执行上述操作

n    			[0000 0100 1001 0000 1000 1000 1110 0100]
n-1  			[0000 0100 1001 0000 1000 1000 1110 0011]
n& (n - 1) =    [0000 0100 1001 0000 1000 1000 1110 0000]

可以看到此时n&(n - 1)的结果是比n少了一个1，此时我们令n = n &(n - 1)，继续执行上述操作，循环下去，就可以统计到1的位数。

那么什么时候停下来？很显然当n都变成0时，否则就说明数据中是由1，就可以继续循环了。所以停止条件时n == 0，n 的二进制表示的全部位数都是0，代码也很好写的🤔。

 /**
     * 方法2：根据1的数量循环
     *
     * @param n
     * @return
     */
    public static int hammingWeight2(int n) {
        int count = 0;
        while(n != 0){
            n = n & (n - 1);
            count ++;
        }
        return count;
    }

上面的两种解法，第一种循环的次数取决于原始数字的位数，而第二种的取决于1的个数，效率明显要快得多，使用n = n & (n - 1)计算是位运算的一个经典技巧，该结论也完美使用与下面的题目：

1.2 比特位计算

参考题目介绍：338. 比特位计数 - 力扣（LeetCode）

最直观的方法就是从0到num的每个数直接计算一下“1的个数”。每个int的数都可以用32的二进制位数表示，只要遍历其二进制表示的每一位即可得到1的数目：

	/**
         * 方法1：统一移位统计
         *
         * @param num
         * @return
         */
    public static int[] countBits(int num) {
        int[] bits = new int[num + 1];
        for(int i = 0; i <= num; i++){
            for(int j = 0; j < 32; j++){
                bits[i] += (i >> j) & 1;
            }
        }
        return bits;
    }

结合上面学来的技巧，可以快速提升速度。与位运算（&）的性质：对于任意整数x，令 x = x & （x - 1），该运算将x的二进制表示的最后一个1 变成0.因此，对于x重复该操作，直到将x变为0，则操作次数就是x的【移位比特数】

	/**
     * 方法2：通过技巧x &= (x - 1);计算
     *
     * @param num
     * @return
     */
    public static int[] countBits2(int num) {
        int[] bits = new int[num+1];
        for(int i=0; i<=num; i++){
            bits[i] = countOnes(i);
        }
        return bits;
    }

    private static int countOnes(int num) {
        int count = 0;
        while(num != 0){
            num = num &(num - 1);
            count++;
        }
        return count;
    }

有没有发现比特位计算和1的个数计算规则是一样的？这就是为什么我么你说了解一道题，就可以解决很多题目。

1.3 颠倒无符号整数

参考题目介绍：190. 颠倒二进制位 - 力扣（LeetCode）

首先这里说的是无符号位，也就是说不用考虑正负的问题，最高位的1也不代表符号位，这就省了一些麻烦。

我们注意到对于n的二进制表示的从低位到高位第i位，在颠倒之后变成第31 - i 位（ 0 <= i < 32)，所以可以从低位到高位遍历n的二进制表示的每一位，将其放在颠倒之后的位置，最后相加就可以了。

看一个栗子🌰，方便演示，我们去较短的16位：

原始数据：  [1001 1111 0000 0110](低位)
    第一步：获取n的最低为0，然后将其右移16-1位15位，得到：
 reversed: [0***  **** **** ****]
 n右移移位： [0100 1111 1000 0011]
    第二步：继续获取n的最低为0，然后将其右移15-1位14位，并于reversed相加得到：
 reversed: [01**  **** **** ****]
 n右移移位： [0010 0111 1100 0001]
     ......
 
     继续直到n全部变成0：
     

理解之后，实现起来就比较容以了。由于Java不存在无符号类型，所有的便是整数的类型都是有符号类型的，因此需要区分算术右移和逻辑右移，在Java中，算术右移的符号是>>，逻辑右移的符号是>>>。

	/**
         * 通过移位实现反转
         *
         * @param n
         * @return
         */
    public static int reverseBits(int n) {
       int reversed = 0, power = 31;
       while(n != 0){
           reversed += (n & 1) << power;
           n >>>= 1;
           power--;
       }
       return reversed;
    }

本题还有其他解法，有一种分块的思想，n的二进制表示有32位，可以将n的二进制表示成较小的块，然后将每个块的二进制分别颠倒，最后将每个块的结果合并得到最中的结果。当然这个也是分治的策略。将n的32位二进制便是分成两个16位的块，并将这两个块颠倒；然后对每个16位的块重复上述操作，直到达到位1位的块，我们这里演示一下：

具体的做法如下：

下面的代码中，每一行分别将n分成16位，8位，4位，2位，1位的块，即把每个块分成较小的块，并将分成的两个较小的块颠倒。同时需要注意，使用Java实现是，右移运算必须使用逻辑右移。由于固定的32位，我们可以不必写循环或者递归，可以直接写。

/**
     * 通过分块实现反转
     *
     * @param n
     * @return
     */
    public static int reverseBits2(int n) {
        n = (n >>> 16) | (n << 16);
        n = ((n & 0xFF00FF00) >>> 8) | ((n & 0x00FF00FF) << 8);
        n = ((n & 0xF0F0F0F0) >>> 4) | ((n & 0x0F0F0F0F) << 4);
        n = ((n & 0xCCCCCCCC) >>> 2) | ((n & 0x33333333) << 2);
        n = ((n & 0xAAAAAAAA) >>> 1) | ((n & 0x55555555) << 1);
        return n;
    }

这种方法在JDK、Dubbo等源码中都可以见到，特别是涉及协议解析的场景几乎都不少这样的操作。积累相关的技巧，可以方便面试，也有助于阅读源码。（面试算法和工程算法）。

2. 位实现加减乘除专题

在计算机中，位运算的效率比加减乘除的效率要高，因此在高性能软件的源码中大量应用，而且计算机里的各种操作本质上也是位运算。这里就研究下相关问题。

2.1 位运算实现加法

参考题目介绍：371. 两整数之和 - 力扣（LeetCode）

既然不能使用+和-，那么只能使用位运算了。我们看一下位运算的相加的情况：

[1] 0 + 0 = 0
[2] 0 + 1 = 1
[3] 1 + 0 = 1
[4] 1 + 1 = 0 (发生了位移，这里应该是10 相当于进位)

两个位相加的时候，我们无非要考虑两个问题：进位部分是是么，不知道进位部分是什么。从上面的结果可以看到，对于a和b两个数不进位部分的情况是：相同为0，不同为1，这个不就是a^b吗？

而对于进位，我们发现只有a和b都是1的时候才回进位，而且进位只有1，这不就是a&b = 1吗？然后位数由1位变成了两位，也就是上面的[4]的样子，那么将1向前挪一下呢？手动位移一下就好了，也就是（a&b) << 1。所以我们得出两条结论：

• 不进位的部分：用a^b计算就可以了。
• 是否进位：已经进位值使用（a & b) << 1计算就可以了。

于是，我们可以将整数a和b的和，拆分位a和b的无进位加法结果与进位结果的和。

代码也是很简单：

    
	public int getSum(int a, int b) {
        while(b != 0){
            int sign = (a & b) << 1;
            a = a ^ b;
            b = sign;
        }
        return a;
    }

2.2 递归乘法

参考题目地址：面试题 08.05. 递归乘法 - 力扣（LeetCode）

如果不让用*来计算，一种是将一个作为循环的参数，对另一个进行累加，但是这样的效果太低了,所以要考虑位运算。

首先，求得A和B得最小值和最大值，其中得最小值当做乘数（为什么要选最小值呢，因为选择最小值乘的次数少，可以说算的少），将其拆成分成2得幂得和，即min = a_0 * 2^0+a_1*2_1+…+a_i *2 ^ i + …其中a_i取0或者1。其实就是用二进制得视角取看待min，比如12得二进制表示可以是[0000 1100]也就说是1000 + 0100。就比如这样：

13*12 = 13 * (8 + 4) = 13 * 8 + 13 * 4 = (13 << 3) + (13 << 2);

上面仍需要左移5次，存在重复计算，可以进一步简化：

假设我们需要的结果是ans：

定义临时变量：temp = 13 << 2 = 52 计算之后，可以先让ans = 52；

然后temp继续左移一次 temp = 52 << 1 = 104，此时再让ans = ans + temp

这样只需要执行三次位移和一次加法，实现代码：

  public int multiply(int A, int B) {
        int min = Math.min(A,B);
        int max = Math.max(A,B);
        int ans = 0;
        for(int i = 0; min != 0;i++){
            // 只有当位1 的时候才使用加
            if((min & 1) == 1){
                ans += max;
            }
            min >>= 1;
            max += max;
        }
        return ans;
    }

拓展：

你可以尝试尝试除法，推荐题目：29. 两数相除 - 力扣（LeetCode）

---

总结

提示：位运算技巧；位运算高频题目；相加和相乘；翻转和递归：

---

如果有帮助到你，请给题解点个赞和收藏，让更多的人看到 ~ ("▔□▔)/

如有不理解的地方，欢迎你在评论区给我留言，我都会逐一回复 ~

也欢迎你 关注我 ，喜欢交朋友，喜欢一起探讨问题