目录
冒泡排序
优化:
堆排序
插入排序
希尔排序
归并排序
快速排序
优化
选择排序
排序算法的稳定性: 大小相同的元素在排序前后相对位置相同就称其为稳定的排序。
注:一个本身就是稳定的排序 是可以实现为不稳定的排序的 ;但是相反 一个本身就不稳定的排序 是不可能实现为稳定的排序的。
稳定的排序算法:插入排序 冒泡排序 归并排序
冒泡排序
时间复杂度: o(n^2) 如果加了优化 最好情况O(N)
空间复杂度:O(1)
稳定性: 稳定
public static void bubbleSort(int[] array){
for (int i = 0; i < array.length-1; i++) {
for (int j = 0; j < array.length-1; j++) {
if (array[j] > array[j+1]) {
swap(array, j, j+1);
}
}
}
}
private static void swap(int[] array, int minIndex, int i) {
int tmp = array[i];
array[i] = array[minIndex];
array[minIndex] = tmp;
}优化:
public static void bubbleSort(int[] array) {
for (int i = 0; i < array.length-1; i++) {
boolean flg = false;
for (int j = 0; j < array.length-1-i; j++) {
if(array[j] > array[j+1]) {
swap(array,j,j+1);
flg = true;
}
}
if(!flg) {
return;
}
}
}堆排序
时间复杂度:O(n*logN) N^1.3 -->
空间复杂度:O(1)
稳定性:不稳定
数据量非常 大的时候 堆排 一定比希尔快
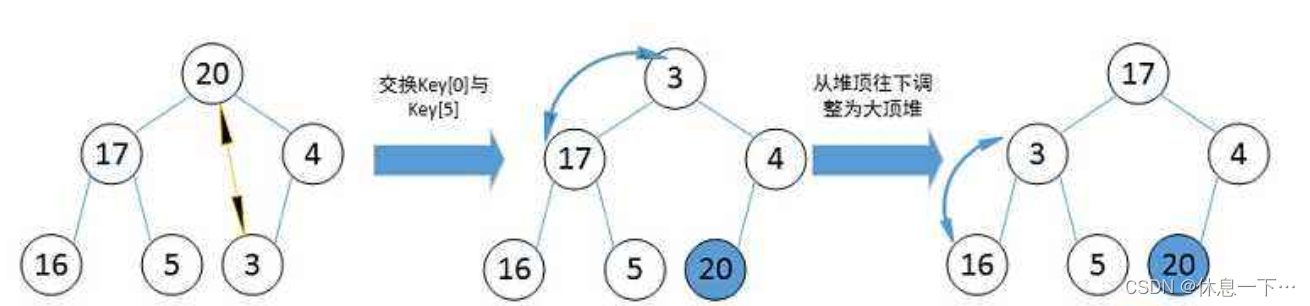
堆排序的原理:
- 用一个大根堆的堆顶元素和最后一个元素交换
- 使数组长度减一
- 在重新将堆调整为大根堆
public static void heapSort(int[] array){
createHeap(array);
for (int i = 0; i < array.length - 1; i++) {
swap(array, 0, array.length-1-i);
shiftDown(array, 0, array.length-1-i);
}
}
private static void createHeap(int[] array) {
for (int i = (array.length-1-1)/2; i >= 0; i--) {
shiftDown(array, i, array.length);
}
}
private static void shiftDown(int[] array, int i, int length) {//length个元素
int child = i * 2 + 1;
while (child < length) {
if (child + 1 < length && array[child] < array[child+1]) {
child++;
}
if (array[child] > array[i]) {
swap(array, child, i);
i = child;
}else {
break;
}
child = i * 2 + 1;
}
}
private static void swap(int[] array, int minIndex, int i) {
int tmp = array[i];
array[i] = array[minIndex];
array[minIndex] = tmp;
}插入排序
时间复杂度:
最好情况:数据完全有序的时候 O(N)
最坏情况:数据完全逆序的时候 O(N^2)
空间复杂度:O(1)
稳定性:稳定
插入排序的原理
- 从左边第一位开始挨个令其成为关键码
- 从左到右把待排序的记录按其关键码值的大小逐个插入到左边已经排好序的有序序列中
- 直到所有的记录插入完为止,得到一个新的有序序列
public static void insertSort(int[] array){
for (int i = 1; i < array.length; i++) {
int tmp = array[i];
int j = i - 1;
for (; j >= 0 ; j--) {
//如果此处改为array[j] >= tmp就会变成不稳定排序
if (array[j] > tmp) {
array[j+1] = array[j];
}else{
break;
}
}
array[j+1] = tmp;
}
}希尔排序
时间复杂度:
约等于:n^1.3 - n^1.5
复杂度:O(1)
稳定性:不稳定希尔排序其实就是对插入排序的一种优化
基本原理:
- 先按照步长将数组分为若干组
- 对每组进行插入排序
- 减小步长重复以上步骤
public static void shellSort(int[] array){
int gap = array.length;
while (gap > 1) {
gap = gap / 2;
shell(array, gap);
}
}
private static void shell(int[] array, int gap) {
for (int i = gap; i < array.length; i++) {
int tmp = array[i];
int j = i-gap;
for (; j >= 0; j -= gap) {
if (array[j] > tmp) {
array[j+gap] = array[j];
}else {
break;
}
}
array[j+gap] = tmp;
}
}归并排序
时间复杂度: 0(N*logN)
空间复杂度:O(n)
稳定性: 稳定归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。
可参考:
http://t.csdnimg.cn/Yd62c
public void mergerSort(int[] nums, int left, int right) {//right:数组长度减一
if (left >= right) {
return;
}
int mid = (left + right) / 2;
mergerSort(nums, left, mid);
mergerSort(nums, mid + 1, right);
merger(nums, left, mid, right);
}
private void merger(int[] nums, int left, int mid, int right) {
int[] tmp = new int[right-left+1];
int i = 0;
int l = left;
int r = mid + 1;
while (l <= mid && r <= right) {
if (nums[l] < nums[r]) {
tmp[i++] = nums[l++];
}else {
tmp[i++] = nums[r++];
}
}
while (l <= mid) {
tmp[i++] = nums[l++];
}
while (r <= right) {
tmp[i++] = nums[r++];
}
i = 0;
for (int j = 0; j < tmp.length; j++) {
nums[left++] = tmp[j];
}
}快速排序
时间复杂度:
最好情况:O(N*logN) 满二叉树/完全二叉树
最坏情况:O(N^2) 单分支的树
空间复杂度:
最好情况:O(logN) 满二叉树/完全二叉树
最坏情况:O(N) 单 分支的树
稳定性:不稳定快速排序基本原理
- 任取待排序元素序列中的某元素作为基准值
- 按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值
- 每个子序列重复该过程,直到所有元素都排列在相应位置上为止
有Hoare法 挖坑版法 前后指针法
这里只介绍Hoare法
public static void quickSort(int[] array){
quick(array, 0, array.length-1);
}
private static void quick(int[] array, int left, int right) {
if (left >= right) {
return;
}
int Index = findSwap(array, left, right);
quick(array, left, Index-1);
quick(array, Index+1, right);
}
private static int findSwap(int[] array, int left, int right) {
int key = array[left];
int keyIndex = left;
while (left < right) {
//必须right先走
//如果是left先走,两个相遇的地方一定比key大
while (left < right && array[right] >= key) {
right--;
}
while (left < right && array[left] <= key) {
left++;
}
swap(array, right, left);
}
if (left == right) {
swap(array, keyIndex, left);
}
return left;
}
private static void swap(int[] array, int minIndex, int i) {
int tmp = array[i];
array[i] = array[minIndex];
array[minIndex] = tmp;
}优化
利用三数取中法来避免但分支书的形成(尽量降低树的高度)
public int[] sortArray(int[] nums) {
//快速排序
quickSort(nums, 0, nums.length-1);
return nums;
}
private void quickSort(int[] nums, int left, int right) {
if (left >= right) {
return;
}
//三数取中法
swap(nums, left, threeNumMid(nums, left, right));
//也可以在这里加一个判断当左右之间的数据个数小于一定值然后调用插入排序
//因为在排序过程中数组会趋近于有序所以插入排序的效率会很快
int pivot = quick(nums, left, right);
quickSort(nums, left, pivot-1);
quickSort(nums, pivot+1, right);
}
private int threeNumMid(int[] nums, int left, int right) {
int mid = (left + right) / 2;
if (nums[left] > nums[right]) {
if (nums[mid] > nums[left]) {
return left;
}else if (nums[mid] < nums[right]) {
return right;
}else {
return mid;
}
}else {
if (nums[mid] < nums[left]) {
return left;
}else if (nums[mid] > nums[right]) {
return right;
}else {
return mid;
}
}
}
private int quick(int[] nums, int left, int right) {
int index = left;
int key = nums[left];
while (left < right) {
while (left < right && nums[right] >= key) {
right--;
}
while (left < right && nums[left] <= key) {
left++;
}
swap(nums, right, left);
}
swap(nums, index, left);
return left;
}
private void swap(int[] nums, int left, int right) {
int tmp = nums[left];
nums[left] = nums[right];
nums[right] = tmp;
}选择排序
时间复杂度:O(n^2)
空间复杂度:O(1)
稳定性:不稳定的排序选择排序基本原理:
- 从左至右每一次从待排序的数据元素中选出最小(或最大)的一个元素
- 将其放在待排序元素的起始位置,已有序元素的最后边
- 重复上述步骤直到全部待排序的数据元素排完 。
public static void selectSort(int[] array){
for (int i = 0; i < array.length; i++) {
int minIndex = i;
for (int j = i+1; j < array.length; j++) {
if (array[minIndex] > array[j]) {
minIndex = j;
}
}
swap(array, minIndex, i);
}
}
private static void swap(int[] array, int minIndex, int i) {
int tmp = array[i];
array[i] = array[minIndex];
array[minIndex] = tmp;
}

![[BJDCTF2020]The mystery of ip](https://img-blog.csdnimg.cn/444d4f8816e948c98d008dd8c4c461da.png)