1. 题目

        给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

2. 输入输出样例

        示例1

输入：nums = [3,2,3]
输出：3

        示例2

输入：nums = [2,2,1,1,1,2,2]
输出：2

3. 实现思路

        使用分治法来寻找数组中的众数，主要的思路是

        （1）将数组分成左右两半，然后分别递归求解左半部分和右半部分的众数。

        （2）如果左半部分和右半部分的众数相同，那么这个数就是整个数组的众数。

        （3）如果不相同，在区间[l, r]内进行统计左半部分和右半部分各自的众数出现次数，然后返回出现次数较多的众数作为结果。

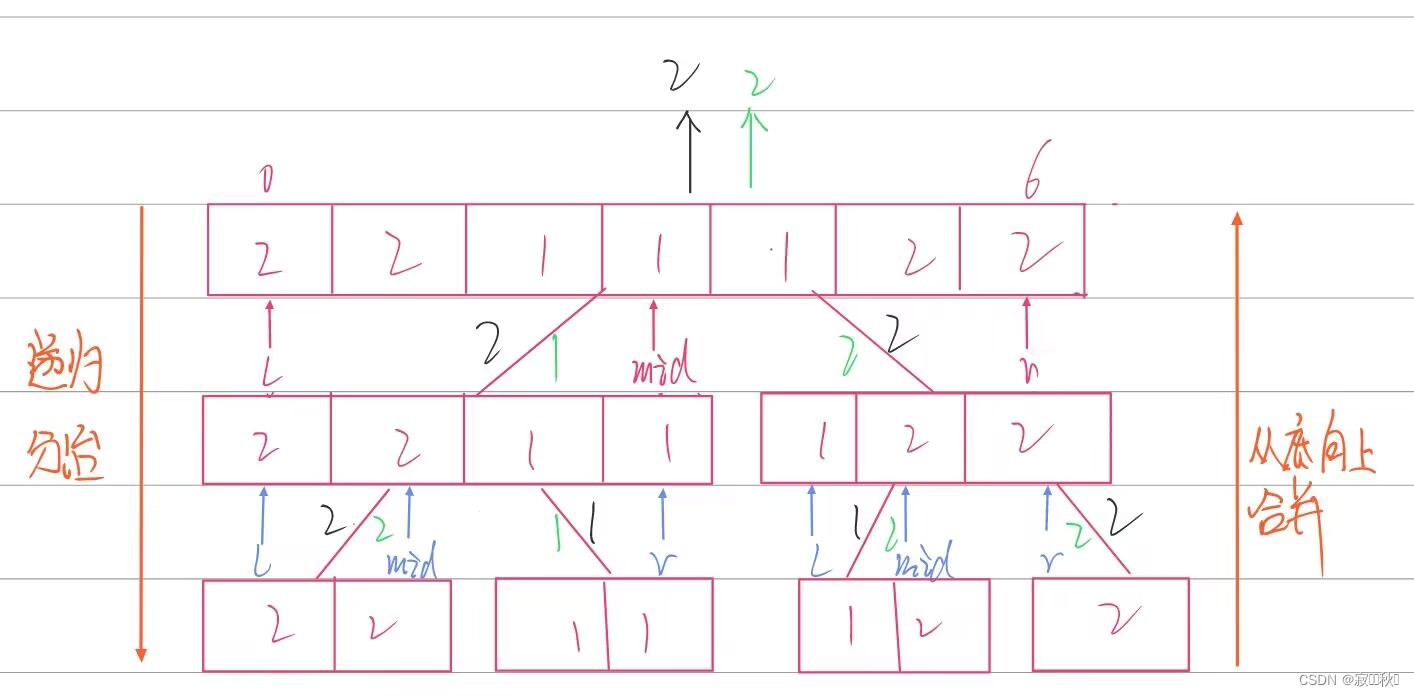
        算法的时间复杂度为 O(nlogn)，其中 n 为数组的大小，因为每次递归都将数组分成两半，总共需要进行 logn层递归，每层递归需要线性时间来统计众数的出现次数。

4. 实现代码

// 采用分治法实现
int zsnum(int* nums, int l, int r){
    // 当递归范围只有一个元素时，直接返回这个元素
    if(l == r){
        return nums[l];
    }
    
    // 计算中间位置
    int mid = (l + r) / 2;
    
    // 分别递归计算左半部分和右半部分的众数
    int zsnuml = zsnum(nums, l, mid);
    int zsnumr = zsnum(nums, mid + 1, r);
    
    // 如果左右两半的众数相同，那么这个数就是整个区间的众数
    if(zsnuml == zsnumr){
        return zsnuml;
    }
    
    // 否则，统计左半部分和右半部分各自的众数出现次数
    int i = l, countl = 0, countr = 0;
    while(i <= r){
        if(nums[i] == zsnuml){
            countl++;
        }
        if(nums[i] == zsnumr){
            countr++;
        }
        i++;
    }
    
    // 返回出现次数较多的众数
    if(countl > countr){
        return zsnuml;
    }
    return zsnumr;
}

// 寻找数组中的众数的入口函数
int majorityElement(int* nums, int numsSize){
    return zsnum(nums, 0, numsSize - 1);
}

169. 多数元素 - 力扣（LeetCode）https://leetcode.cn/problems/majority-element/description/