相关阅读
数字IC前端![]() https://blog.csdn.net/weixin_45791458/category_12173698.html?spm=1001.2014.3001.5482
https://blog.csdn.net/weixin_45791458/category_12173698.html?spm=1001.2014.3001.5482
数字信号处理作为微处理器的核心部件,是决定着总体处理器性能的因素之一,而数字乘法器是最常见的一种数字信号处理电路。通常情况下,乘法器是数字系统中制约运算速度的关键路径。本系列将从基本的乘法器入手,再逐渐深入,探究了各种优化乘法器在体系结构,乘法算法等方面的优化策略。
作为最基本的组合逻辑乘法器,阵列乘法器(Array multiplier)虽然已不太常用,但在某些对性能要求不高的应用场景下,还能见到它的使用。
为了简便起见,本文考虑两个四位二进制数A和B相乘,其中A为被乘数,B为乘数,先产生部分积,然后使用加法器累加这些部分积,总体规划如表1所示。从乘数B的最低位B0开始,依次与被乘数A的各位A0、A1、A2、A3相与(乘)形成4组16个部分积项目,分组是根据乘数B的位而言,如所有有B0项目的是第0组部分积。然后每一组根据分组的不同,移动到乘数B每一位对应的位置,最后将部分积累加。注意,在部分积的累加过程中,可能会出现来自低位的进位,此时需要使用全加器,否则使用半加器即可。
表1 无符号4位二进制乘法规划
| A3 B3 | A2 B2 | A1 B1 | A0 B0 | 被乘数 乘数 | 资源配置 | ||||
| A3B1 C12 | A3B0 A2B1 C11 | A2B0 A1B1 C10 | A1B0 A0B1 | A0B0 | 部分积0 部分积1 低位进位 | 第1行加法器 | |||
| C13 A3B2 C22 | S13 A2B2 C21 | S12 A1B2 C20 | S11 A0B2 | S10 | S00 | 第1行和 部分积2 低位进位 | 第2行乘法器 | ||
| C23 A3B3 C32 | S23 A2B3 C31 | S22 A1B3 C30 | S21 A0B3 | S20 | 第2行和 部分积3 低位进位 | 第3行乘法器 | |||
| C33 | S33 | S32 | S31 | S30 | 第3行和 | ||||
| C33 | S33 | S32 | S31 | S30 | S20 | S10 | S00 | 最终结果 | |
| 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | 权重 |
4位乘法器的组合逻辑结构如图1所示,可以看出这种结构十分规则,大多是由加法器和与门构成的基本单元复制得到,但由红线和紫线描绘的路径可以看出其中存在较长的加法器链(即可能的关键路径),换个角度,结构中使用了3组行波进位加法器(Ripple Carry Adder)或者说串行进位加法器(Serial Carry Adder)、进位传播加法器(Carry Propagate Adder),这种乘法器的优点在于可复用性和可配置性强,非常利于集成电路制造,但缺点是进位操作的关键路径较长,控制组合电路输入输出的时钟周期需要与电路中的最长路径相适应。为了提高性能,可以在这种结构中植入流水线来获得更大的数据吞吐量,这是对组合逻辑优化的一个常见方法。具体的Verilog代码实现见附录,Modelsim软件仿真截图如图2所示。使用Synopsis的综合工具Design Compiler综合的结果如图3所示,综合使用了0.13μm工艺库。
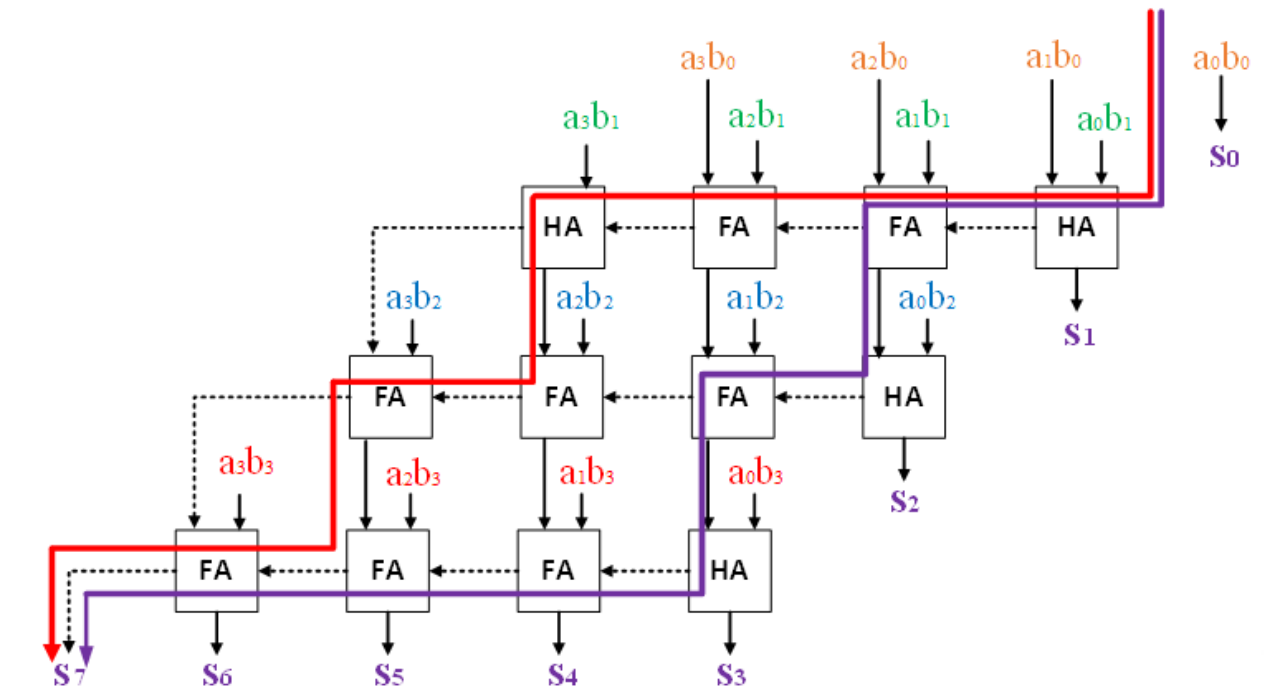
图1 基本单元构成的阵列乘法器

图2 阵列乘法器仿真结果
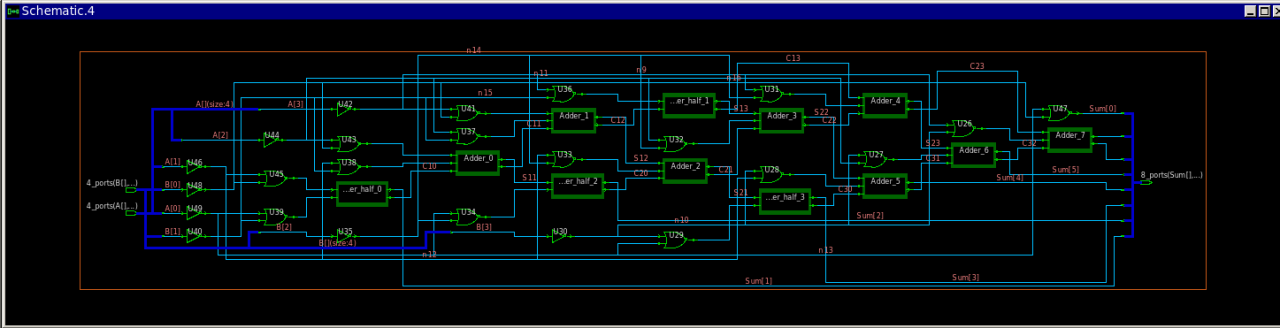
图3 阵列乘法器综合结果
在Design Compiler中使用report_timing命令,可以得到关键路径的延迟,如图4所示,使用report_area命令,报告所设计电路的面积占用情况,如图5所示
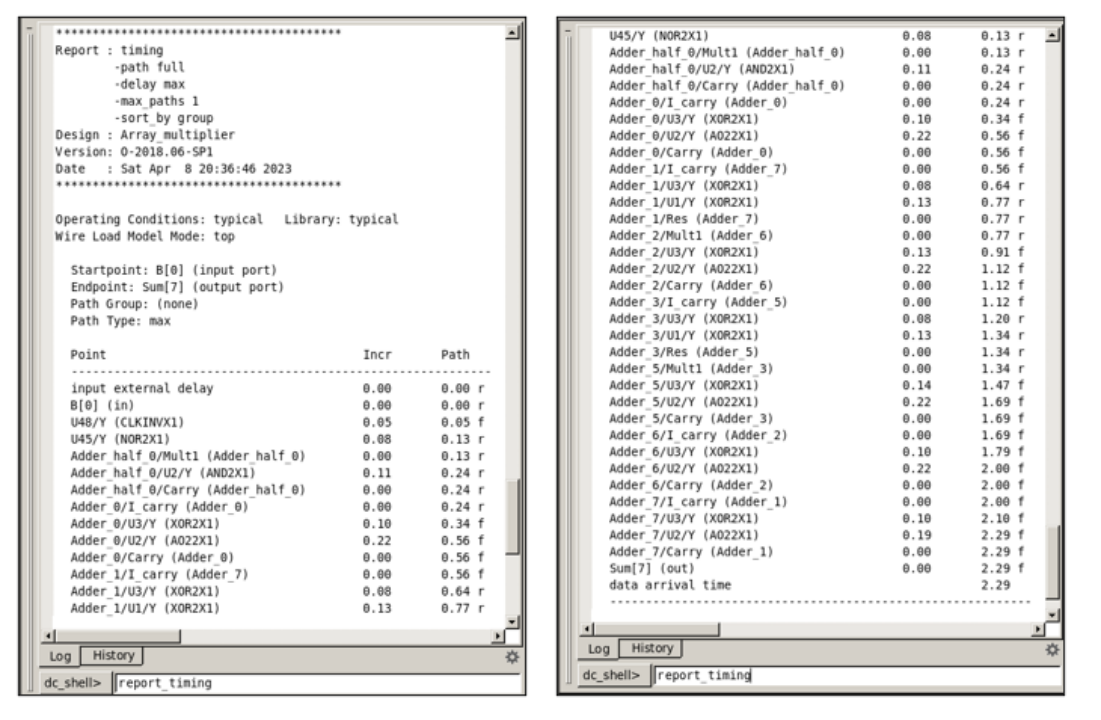
图4 关键路径报告
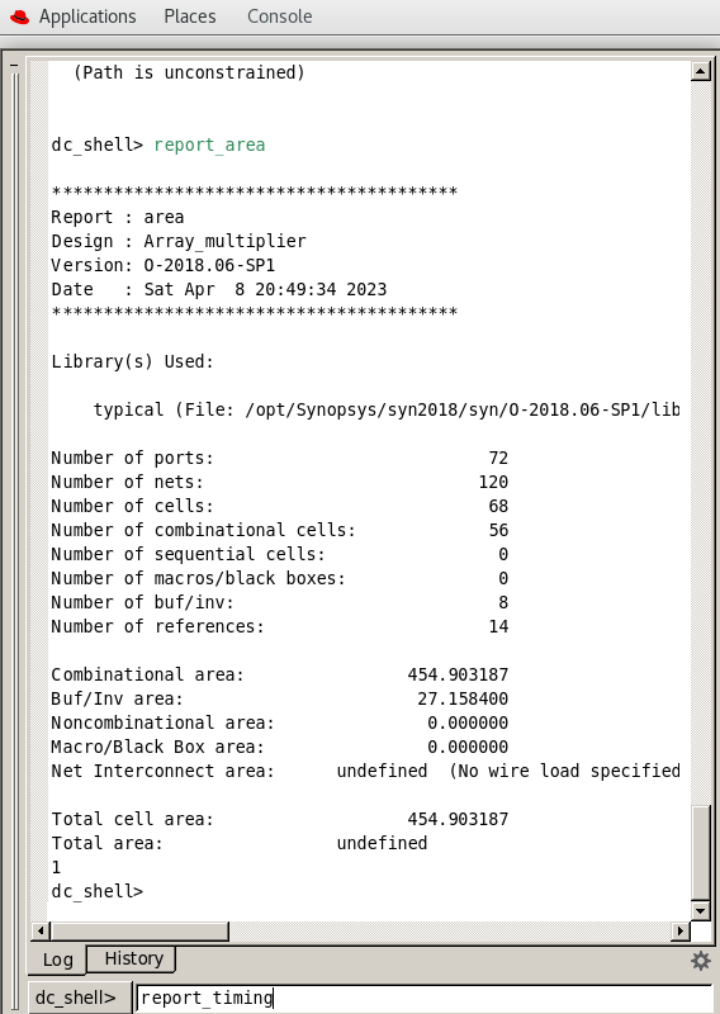
图5 面积报告
阵列乘法器的Verilog代码如下所示。
module Array_multiplier(input [3:0]A,B,output[7:0]Sum);
wire [3:0]partial_product[3:0];
//产生部分积
assign partial_product[0]=B[0]?A:0;
assign partial_product[1]=B[1]?A:0;
assign partial_product[2]=B[2]?A:0;
assign partial_product[3]=B[3]?A:0;
//中间进位
wire C10,C11,C12,C13;
wire C20,C21,C22,C23;
wire C30,C31,C32,C33;
//中间和
wire S11,S12,S13;
wire S21,S22,S23;
//第一行加法器
assign Sum[0]=partial_product[0][0];
Adder_half Adder_half_0(partial_product[0][1],partial_product[1]
[0],Sum[1],C10);
Adder Adder_0(partial_product[0][2],partial_product[1][1],C10,S11,C11);
Adder Adder_1(partial_product[0][3],partial_product[1][2],C11,S12,C12);
Adder_half Adder_half_1(partial_product[1][3],C12,S13,C13);
//第二行乘法器
Adder_half Adder_half_2(S11,partial_product[2][0],Sum[2],C20);
Adder Adder_2(S12,partial_product[2][1],C20,S21,C21);
Adder Adder_3(S13,partial_product[2][2],C21,S22,C22);
Adder Adder_4(C13,partial_product[2][3],C22,S23,C23);
//第三行加法器
Adder_half Adder_half_3(S21,partial_product[3][0],Sum[3],C30);
Adder Adder_5(S22,partial_product[3][1],C30,Sum[4],C31);
Adder Adder_6(S23,partial_product[3][2],C31,Sum[5],C32);
Adder Adder_7(C23,partial_product[3][3],C32,Sum[6],Sum[7]);
Endmodule
module Adder (
input Mult1,
input Mult2,
input I_carry,
output Res,
output Carry
);
assign Res = Mult1 ^ Mult2 ^ I_carry;
assign Carry = (Mult1 & Mult2) | ((Mult1 ^ Mult2) & I_carry);
endmodule
module Adder_half (
input Mult1,
input Mult2,
output Res,
output Carry
);
assign Res = Mult1 ^ Mult2;
assign Carry = Mult1 & Mult2;
endmodule