一、说明

        逻辑回归模型是处理分类问题的最常见机器学习模型之一。二项式逻辑回归只是逻辑回归模型的一种类型。它指的是两个变量的分类，其中概率用于确定二元结果，因此“二项式”中的“bi”。结果为真或假 — 0 或 1。

        二项式逻辑回归的一个例子是预测人群中 COVID-19 的可能性。一个人要么感染了COVID-19，要么没有，必须建立一个阈值以尽可能准确地区分这些结果。

二、sigmoid函数

        这些预测不适合一条线，就像线性回归模型一样。相反，逻辑回归模型拟合到右侧所示的 sigmoid 函数。

        对于每个 x，生成的 y 值表示结果为 True 的概率。在 COVID-19 示例中，这表示医生对某人感染病毒的信心。在右图中，阴性结果为蓝色，阳性结果为红色。

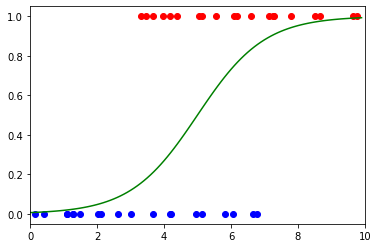
图片来源：作者

三、过程

        要进行二项式逻辑回归，我们需要做各种事情：

1. 创建训练数据集。
2. 使用 PyTorch 创建我们的模型。
3. 将我们的数据拟合到模型中。

        逻辑回归问题的第一步是创建训练数据集。首先，我们应该设置一个种子来确保我们的随机数据的可重复性。

import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
from torch.nn import Linear

torch.manual_seed(42)   # set a random seed

我们必须使用 PyTorch 的线性模型，因为我们正在处理一个输入 x 和一个输出 y。因此，我们的模型是线性的。为此，我们将使用 PyTorch 的函数：Linear

model = Linear(in_features=1, out_features=1) # use a linear model

接下来，我们必须生成蓝色 X 和红色 X 数据，确保将它们从行向量重塑为列向量。蓝色的在 0 到 7 之间，红色的在 7 到 10 之间。对于 y 值，蓝点表示 COVID-19 测试阴性，因此它们都将是

1. 对于红点，它们代表 COVID-19 测试呈阳性，因此它们将为 1。下面是代码及其输出：

blue_x = (torch.rand(20) * 7).reshape(-1,1)   # random floats between 0 and 7
blue_y = torch.zeros(20).reshape(-1,1)

red_x = (torch.rand(20) * 7+3).reshape(-1,1)  # random floats between 3 and 10
red_y = torch.ones(20).reshape(-1,1)

X = torch.vstack([blue_x, red_x])   # matrix of x values
Y = torch.vstack([blue_y, red_y])   # matrix of y values

现在，我们的代码应如下所示：

import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
from torch.nn import Linear

torch.manual_seed(42)   # set a random seed

model = Linear(in_features=1, out_features=1) # use a linear model

blue_x = (torch.rand(20) * 7).reshape(-1,1)   # random floats between 0 and 7
blue_y = torch.zeros(20).reshape(-1,1)

red_x = (torch.rand(20) * 7+3).reshape(-1,1)  # random floats between 3 and 10
red_y = torch.ones(20).reshape(-1,1)

X = torch.vstack([blue_x, red_x])   # matrix of x values
Y = torch.vstack([blue_y, red_y])   # matrix of y values

四、优化

        我们将使用梯度下降过程来优化 S 形函数的损失。损失是根据函数拟合数据的优度计算的，数据由 S 形曲线的斜率和截距控制。我们需要梯度下降来找到最佳斜率和截距。

        我们还将使用二进制交叉熵（BCE）作为我们的损失函数，或对数损失函数。对于一般的逻辑回归，不包含对数的损失函数将不起作用。

        为了实现BCE作为我们的损失函数，我们将它设置为我们的标准，并将随机梯度下降作为我们优化它的手段。由于这是我们将要优化的函数，我们需要传入模型参数和学习率。

epochs = 2000   # run 2000 iterations
criterion = nn.BCELoss()    # implement binary cross entropy loss function

optimizer = torch.optim.SGD(model.parameters(), lr = .1) # stochastic gradient descent

        现在，我们准备开始梯度下降以优化我们的损失。我们必须将梯度归零，通过将我们的数据插入 sigmoid 函数来找到 y-hat 值，计算损失，并找到损失函数的梯度。然后，我们必须迈出一步，确保存储我们的新斜率并为下一次迭代进行拦截。

optimizer.zero_grad()
Yhat = torch.sigmoid(model(X)) 
loss = criterion(Yhat,Y)
loss.backward()
optimizer.step() 

五、收尾

        为了找到最佳斜率和截距，我们本质上是在训练我们的模型。我们必须对多次迭代或纪元应用梯度下降。在此示例中，我们将使用 2,000 个纪元进行演示。

epochs = 2000   # run 2000 iterations
criterion = nn.BCELoss()    # implement binary cross entropy loss function

optimizer = torch.optim.SGD(model.parameters(), lr = .1) # stochastic gradient descent

for i in range(epochs):
    optimizer.zero_grad()
    Yhat = torch.sigmoid(model(X))
    loss = criterion(Yhat,Y)
    loss.backward()
    optimizer.step()

    print(f"epoch: {i+1}")
    print(f"loss: {loss: .5f}")
    print(f"slope: {model.weight.item(): .5f}")
    print(f"intercept: {model.bias.item(): .5f}")
    print()

将所有代码片段放在一起，我们应该得到以下代码：

import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
from torch.nn import Linear

torch.manual_seed(42)   # set a random seed

model = Linear(in_features=1, out_features=1) # use a linear model

blue_x = (torch.rand(20) * 7).reshape(-1,1)   # random floats between 0 and 7
blue_y = torch.zeros(20).reshape(-1,1)

red_x = (torch.rand(20) * 7+3).reshape(-1,1)  # random floats between 3 and 10
red_y = torch.ones(20).reshape(-1,1)

X = torch.vstack([blue_x, red_x])   # matrix of x values
Y = torch.vstack([blue_y, red_y])   # matrix of y values

epochs = 2000   # run 2000 iterations
criterion = nn.BCELoss()    # implement binary cross entropy loss function

optimizer = torch.optim.SGD(model.parameters(), lr = .1) # stochastic gradient descent

for i in range(epochs):
    optimizer.zero_grad()
    Yhat = torch.sigmoid(model(X))
    loss = criterion(Yhat,Y)
    loss.backward()
    optimizer.step()

    print(f"epoch: {i+1}")
    print(f"loss: {loss: .5f}")
    print(f"slope: {model.weight.item(): .5f}")
    print(f"intercept: {model.bias.item(): .5f}")
    print()
两千个时期后的最终输出：

epoch: 2000
loss:  0.53861
slope:  0.61276
intercept: -3.17314

两千个时期后的最终输出：

epoch: 2000
loss:  0.53861
slope:  0.61276
intercept: -3.17314 

六、可视化

        最后，我们可以将数据与 sigmoid 函数一起绘制，以获得以下可视化效果：

x = np.arange(0,10,.1)
y = model.weight.item()*x + model.bias.item()

plt.plot(x, 1/(1 + np.exp(-y)), color="green")

plt.xlim(0,10)
plt.scatter(blue_x, blue_y, color="blue")
plt.scatter(red_x, red_y, color="red")

plt.show()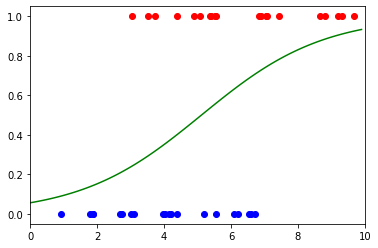

图片来源：作者

七、局限性

        二元分类的最大问题之一是需要阈值。在逻辑回归的情况下，此阈值应为 x 值，其中 y 为 50%。我们试图回答的问题是将阈值放在哪里？

        在 COVID-19 测试的情况下，原始示例说明了这种困境。如果我们将阈值设置为 x=5，我们可以清楚地看到应该是红色的蓝点和应该是蓝色的红点。

        悬垂的红点称为误报，即模型错误地预测正类的区域。悬垂的蓝点称为假阴性 - 模型错误地预测负类的区域。

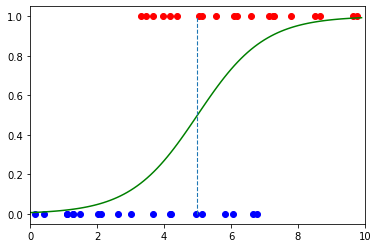
 八、结论

        成功的二项式逻辑回归模型将减少假阴性的数量，因为这些假阴性通常会导致最大的危险。患有COVID-19但检测呈阴性对他人的健康和安全构成严重风险。

        通过对可用数据使用二项式逻辑回归，我们可以确定放置阈值的最佳位置，从而有助于减少不确定性并做出更明智的决策。