LEC 3

1. Contingent Formulas：

定义：Truth or falsity of a propositional formula depends on the truth/falsity of the atoms in the formula

例子：p ∧ q is true if both p and q are true, false otherwise.这里p和q就是atoms，p ∧ q这个公式需要根据p和q的正确性来决定正确性，所以p ∧ q就是contingent formula

2. Valid Formulas：

   a. 定义:

   The formulas that are always true are of special interest,我们叫他valid formulas

   b. 符号：

   c.Valid inference

   d.Validity Summary

3. Finding Valid Inferences Semantically（语义地）

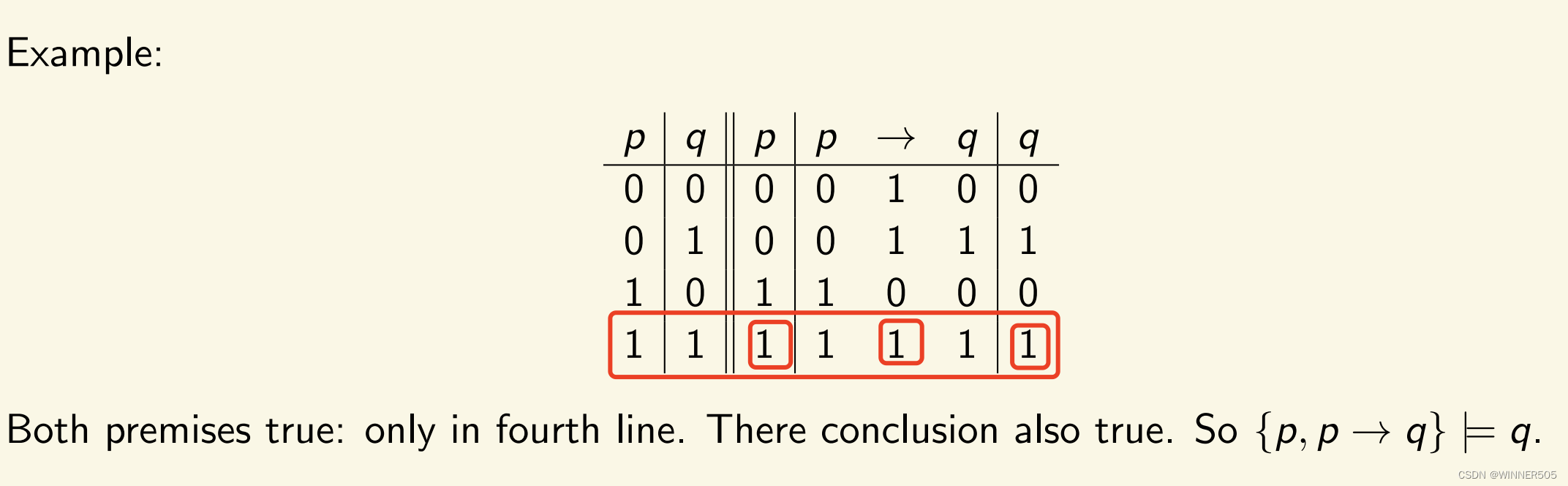
Build “truth tables” for all relevant formulas.

Check whether every row that makes all premises true makes the conclusion true

1. Example of valid

2. Example of non-validity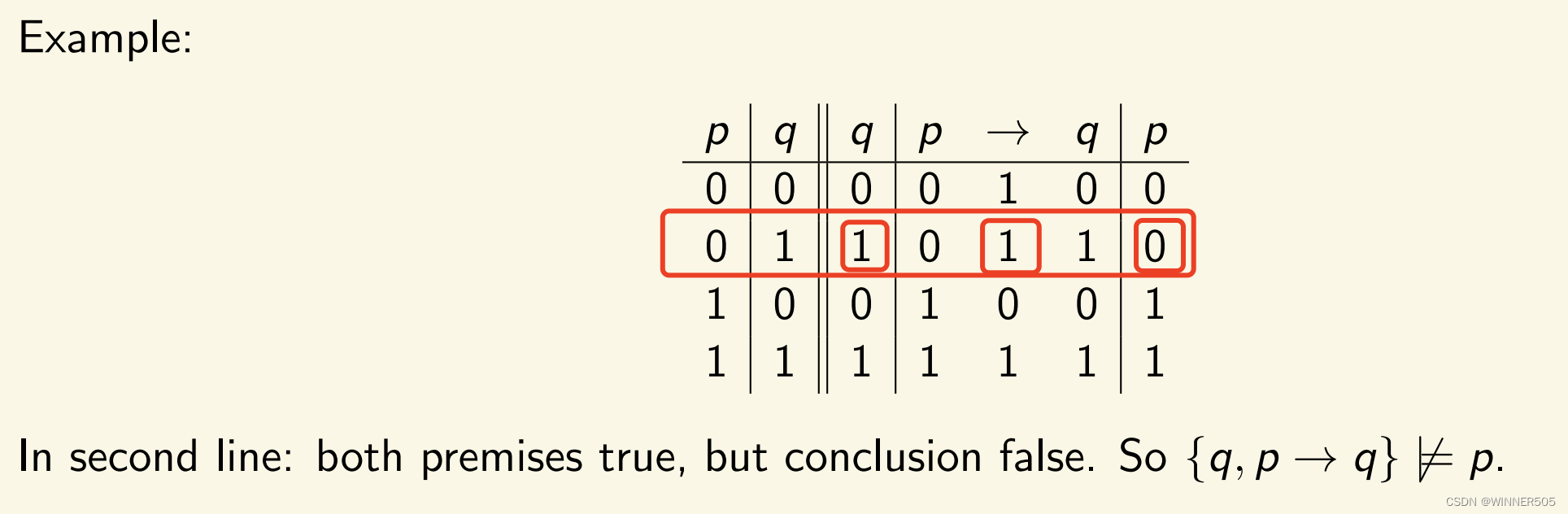

4. Finding Valid Inferences Syntactically(依照语法地)

Alternative method: use a formal proof system

Start with premises and axioms

Derive new valid inferences using an inference rule

5. Abbreviations

 ⊤ and ⊥

Defining ∧,→ and ↔