这篇文章我们来看一下avl树
目录
1.概述
2.AVL树的实现
1.概述
我们前面讲了二叉搜索树,它是有一个key值,然后比父节点key值大的在左边,小的在右边。这样设计是为了便于查找。但是有一种极端的情况,就是所有的结点都在一边,那查找的时间复杂度和在链表的查找时间复杂度就一样了。那有没有解决方法呢?有!
为了解决上述的问题,人们提出了一种新的概念:平衡二叉树
平衡二叉树:它且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树,avl树是平衡二叉树的一种。
这个方案很好的解决了二叉查找树退化成链表的问题,把插入,查找,删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间,不过相对二叉查找树来说,时间上稳定了很多。

如上图所示,就是一个典型的平衡二叉树。
当平衡二叉树添加或删除节点失去平衡的时候,它就进行自选,从而使自己达到平衡。
下面说一下旋转:
左旋:当根节点的右子树的高度减去左子树的高度大于1时,此时二叉树(肯定是二叉搜索树)不平衡了,需要左旋转。具体做法是:以当前根节点的右孩子为新的根节点,当前跟结点及其左子树为新根节点的左孩子,如果新的根节点原本就有左孩子,则其左孩子作为新根节点的新左孩子的右孩子。

右旋:当根节点的左子树的高度减去右子树的高度大于1时,此时二叉树(肯定是二叉搜索树)不平衡了,需要左旋转。具体做法是:以当前根节点的左孩子为新的根节点,当前跟结点及其右子树为新根节点的右孩子,如果新的根节点原本就有右孩子,则其右孩子作为新根节点的新右孩子的左孩子。

2.AVL树的实现
下面看一下AVL树的实现:
package Tree;
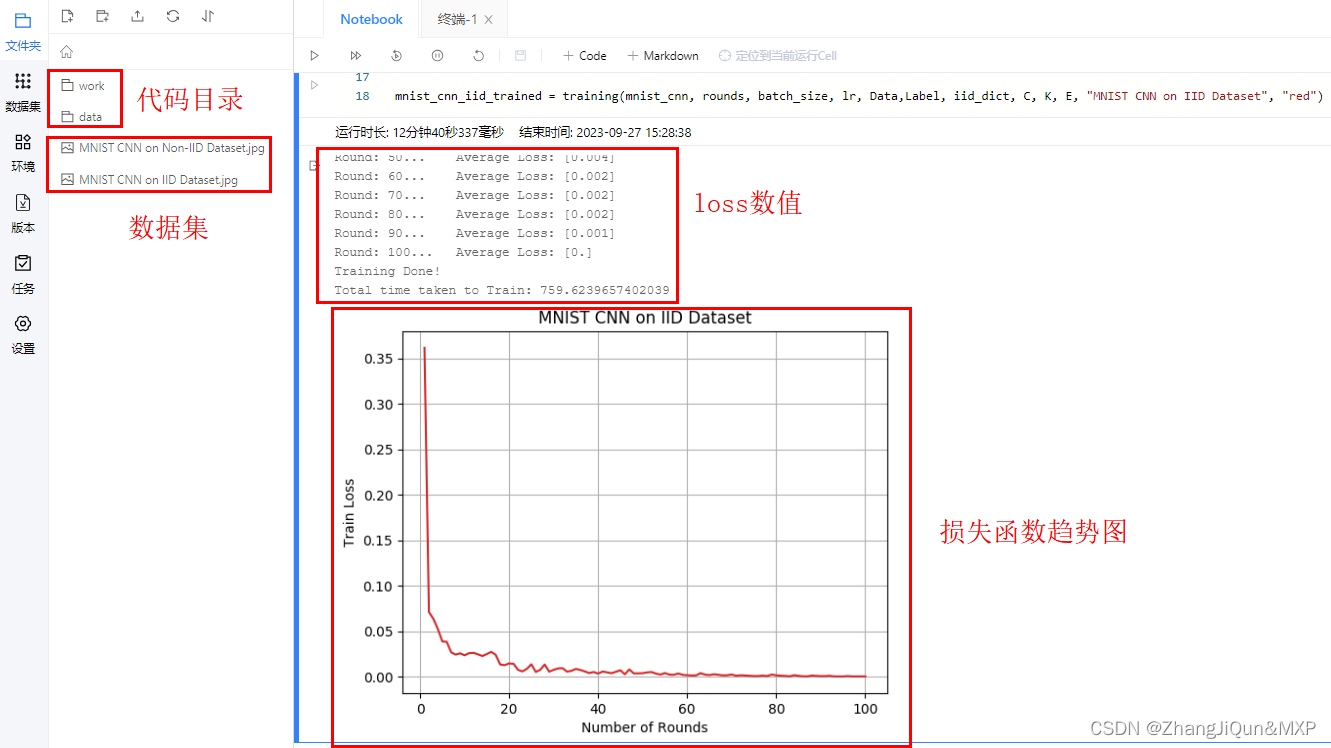
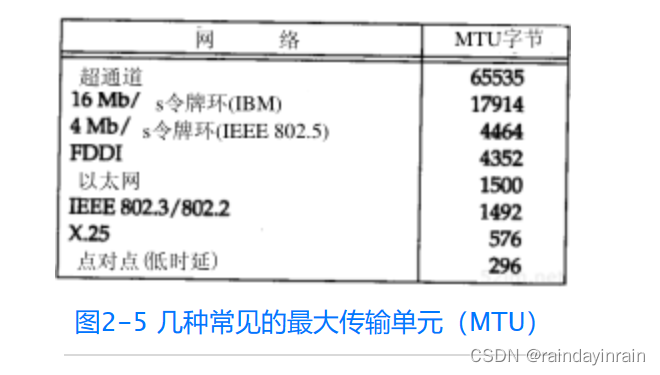
/**AVL树的操作*/
public class L3_AVLTree {
static class AVLNode{
int key;
Object value;
AVLNode left;
AVLNode right;
int height = 1; //高度
public AVLNode(int key, Object value) {
this.key = key;
this.value = value;
}
public AVLNode(int key) {
this.key = key;
}
public AVLNode(int key, Object value, AVLNode left, AVLNode right) {
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
}
/**求节点的高度*/
private int getHeight(AVLNode node){
return node == null? null:node.height;
}
/**更新节点的高度*/
private void updateHeight(AVLNode node){
node.height =
Integer.max(getHeight(node.left),getHeight(node.right))+1;
}
/**求一个节点左右子树的高度差*/
private int bf(AVLNode node){
return (getHeight(node.left) - getHeight(node.right));
}
/**
*右旋
* 参数:失衡的结点(即要选择的结点)
* 返回值:新的根节点
* */
private AVLNode rightRotate(AVLNode node){
AVLNode nodeLeft = node.left;
AVLNode nodeRightLeft = nodeLeft.right;
nodeLeft.right = node;//上位
node.left = nodeRightLeft;//换爹
updateHeight(node);
updateHeight(nodeLeft);
return nodeLeft;
}
/**
* 左旋
* 参数:失衡的结点(即要选择的结点)
* 返回值:新的根节点
* */
private AVLNode leftRotate(AVLNode node){
AVLNode nodeRight = node.right;
AVLNode nodeRightLeft = nodeRight.left;
nodeRight.left = node;//上位
node.right = nodeRightLeft;//换爹
updateHeight(node);
updateHeight(nodeRight);
return nodeRight;
}
/**
* 先左旋左子树,再右旋根节点
* */
private AVLNode leftRightRotate(AVLNode node){
node.left = leftRotate(node.left);
return rightRotate(node);
}
/**
* 先右旋右子树,再左旋根节点
* */
private AVLNode rightLeftRotate(AVLNode node){
node.right = rightRotate(node.right);
return leftRotate(node);
}
/**检查结点是否失衡,如果失衡,则重新平衡结点*/
private AVLNode balance(AVLNode node){
if (node == null){
return null;
}
int bf = bf(node);
if (bf > 1 && bf(node.left) >= 0){//LL
return rightRotate(node);
}else if (bf > 1 && bf(node.left) < 0){//LR
return leftRightRotate(node);
}else if (bf < -1 && bf(node.right) <= 0){//RR
return leftRotate(node);
}else if (bf < -1 && bf(node.right) > 0){//RL
return rightLeftRotate(node);
}
return node;
}
AVLNode root;
/**新增结点*/
public void put(int key,Object value){
root = doPut(root,key,value);
}
private AVLNode doPut(AVLNode node,int key,Object value){
//找到空位,创建新节点
if (node == null){
return new AVLNode(key,value);
}
//key已有,更新操作
if (key == node.key){
node.value = value;
return node;
}
//继续查找
if (key < node.key){
node.left = doPut(node.left,key,value);//向左
}else {
node.right = doPut(node.right,key,value);//向右
}
updateHeight(node);
return balance(node);
}
public void remove(int key){
root = doRemove(root,key);
}
private AVLNode doRemove(AVLNode node,int key){
if (node == null){
return null;
}
//没找到key
if (key < node.key){
node.left = doRemove(node.left,key);
}else if (node.key < key){
node.right = doRemove(node.right,key);
}else { //找到key:没有孩子;只有一个孩子,两个孩子都有
if (node.left == null && node.right == null){
return null;
}else if (node.left == null){
node = node.right;
}else if (node.right == null){
node = node.left;
}else {
AVLNode s = node.right;//后继结点
while (s.left != null){
s = s.left;
}
s.right = doRemove(node.right,s.key);
s.left = node.left;
node = s;
}
}
//更新 高度
updateHeight(node);
//检查失衡
return balance(node);
}
}
总结:会者不难,难者不会。知道定义,会画图,会递归,那就能写出来。然后再查缺补漏一下,就没啥问题。