1. 循环神经网络 RNN( Recurrent Neural Network)
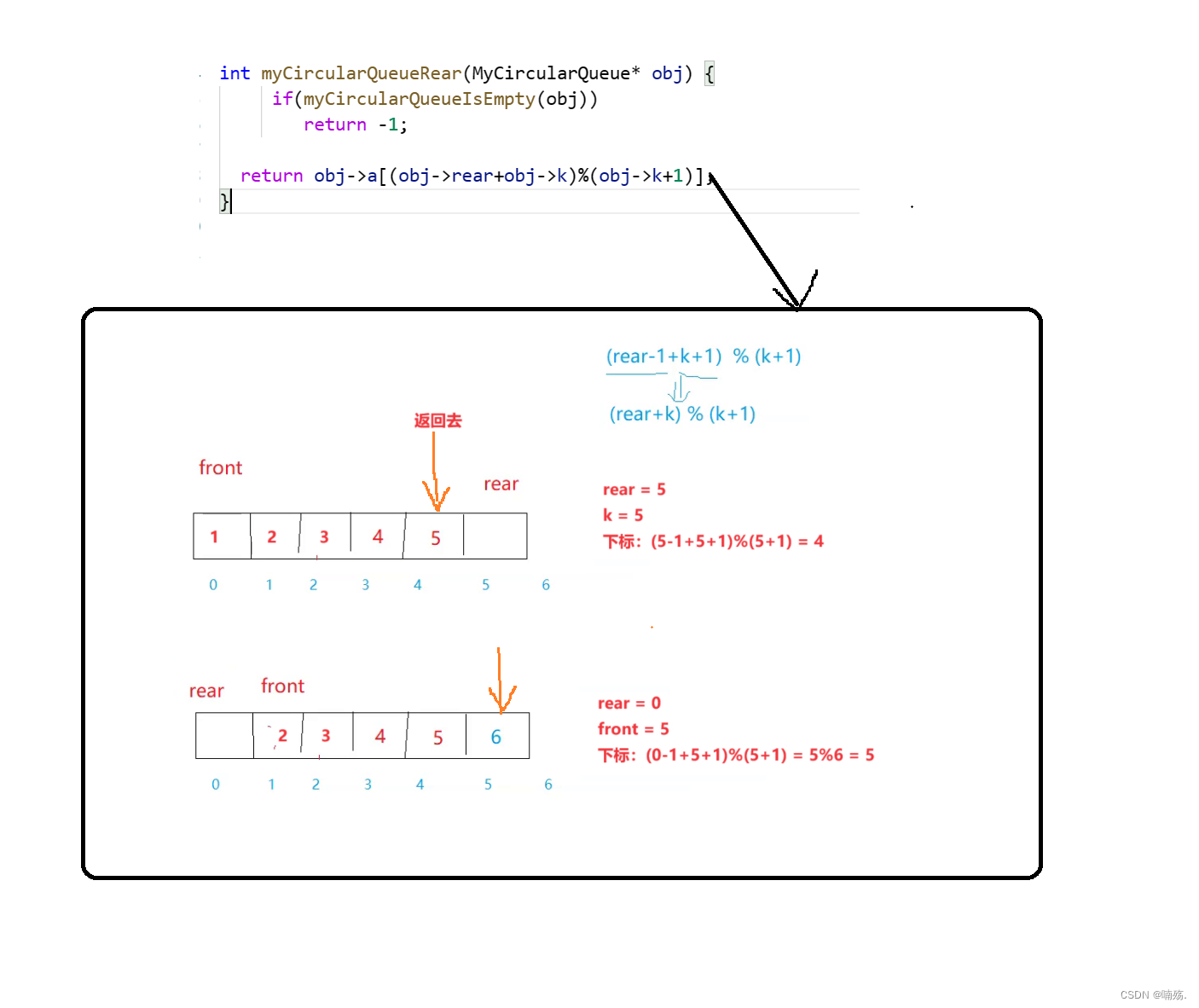
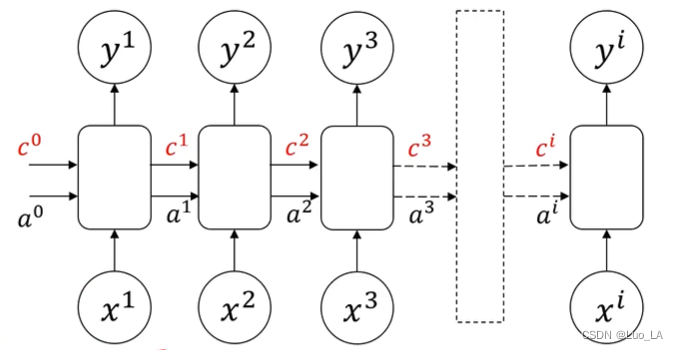
循环神经网络的一个核心是可以把前面的序列数据用到后面的结果预测里面。怎么样实现这一点呢。RNN 结构如下图所示。
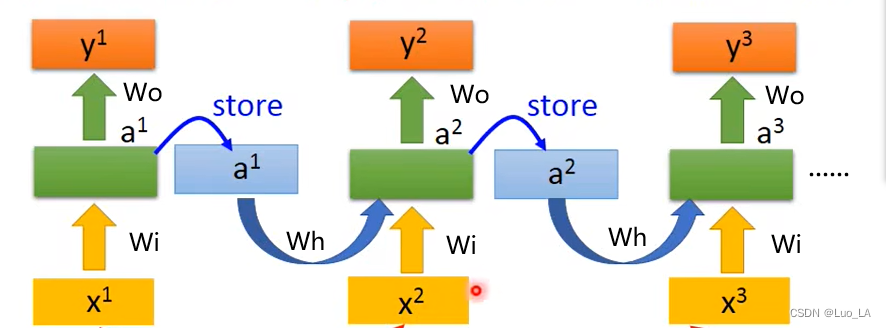
前部序列的信息经处理后,作为输入信息传递到后部序列。
数学模型:
a
1
=
g
a
(
W
h
a
0
+
W
i
x
1
+
b
a
)
a^1=g_a(W_{h}a^0+W_{i}x^1+b_a)
a1=ga(Wha0+Wix1+ba),
y
1
=
g
y
(
W
y
a
0
+
W
o
x
1
+
b
i
)
y^1=g_y(W_{y}a^0+W_{o}x^1+b_i)
y1=gy(Wya0+Wox1+bi)
a
2
=
g
a
(
W
h
a
1
+
W
i
x
2
+
b
a
)
a^2=g_a(W_{h}a^1+W_{i}x^2+b_a)
a2=ga(Wha1+Wix2+ba),
y
2
=
g
y
(
W
y
a
1
+
W
o
x
2
+
b
i
)
y^2=g_y(W_{y}a^1+W_{o}x^2+b_i)
y2=gy(Wya1+Wox2+bi)
……
a
t
=
g
a
(
W
h
a
t
−
1
+
W
i
x
t
+
b
a
)
a^t=g_a(W_{h}a^{t-1}+W_{i}x^t+b_a)
at=ga(What−1+Wixt+ba),
y
t
=
g
y
(
W
y
a
t
−
1
+
W
o
x
t
+
b
i
)
y^t=g_y(W_{y}a^{t-1}+W_{o}x^t+b_i)
yt=gy(Wyat−1+Woxt+bi)
g g g 为激活函数, W , b W,b W,b为训练参数。
2. 不同类型的RNN模型
基本的RNN模型结构
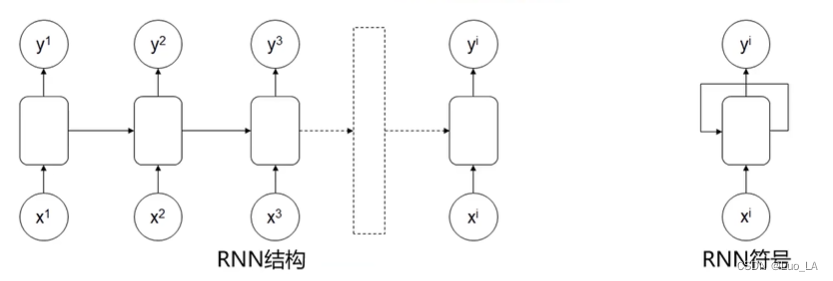
输入:
x
1
,
x
2
,
x
2
,
.
.
.
,
x
i
x^1,x^2,x^2,... ,x^i
x1,x2,x2,...,xi,输出:
y
1
,
y
2
,
y
2
,
.
.
.
,
y
i
y^1,y^2,y^2,... ,y^i
y1,y2,y2,...,yi
多输入对多输出、维度相同RNN结构。
应用:特定信息识别。
多输入单输出RNN结构
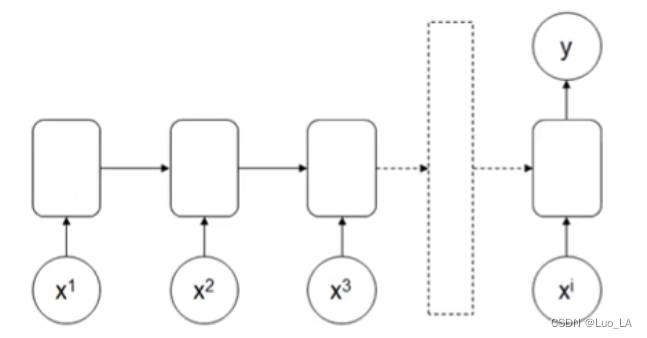
输入:
x
1
,
x
2
,
x
2
,
.
.
.
,
x
i
x^1,x^2,x^2,... ,x^i
x1,x2,x2,...,xi,输出:
y
y
y
应用:情感识别
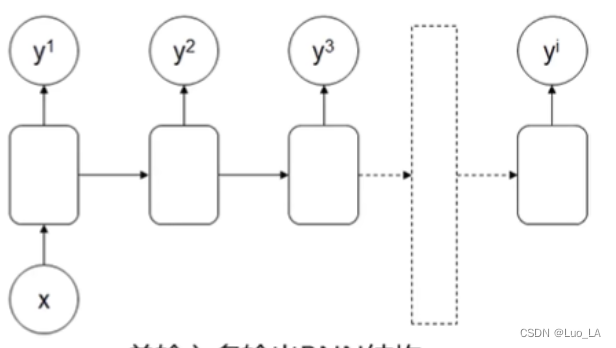
单输入多输出RNN结构
输入:
x
i
xi
xi,输出:
y
1
,
y
2
,
y
2
,
.
.
.
,
y
i
y^1,y^2,y^2,... ,y^i
y1,y2,y2,...,yi
应用:序列数据生成器,如文章生成、音乐生成
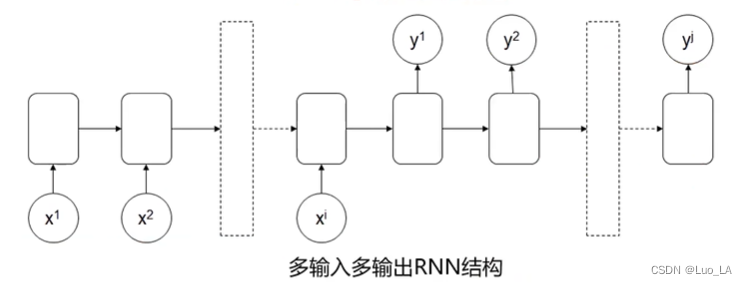
多输入多输出RNN结构
输入:
x
1
,
x
2
,
x
2
,
.
.
.
,
x
i
x^1,x^2,x^2,... ,x^i
x1,x2,x2,...,xi,输出:
y
1
,
y
2
,
y
2
,
.
.
.
,
y
j
y^1,y^2,y^2,... ,y^j
y1,y2,y2,...,yj
应用:语言翻译
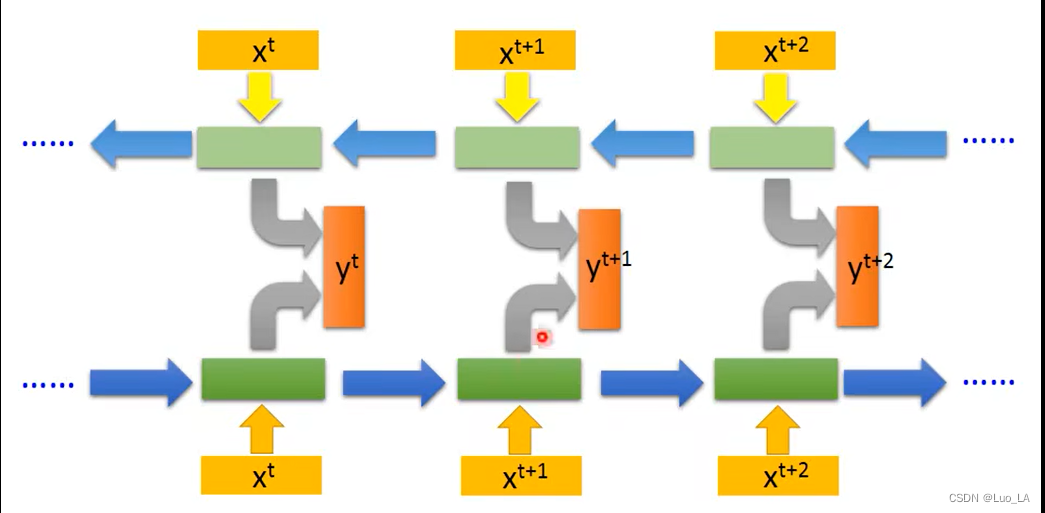
双向循环神经网络(BRNN)
做判断时,把后部序列信息也考虑进去
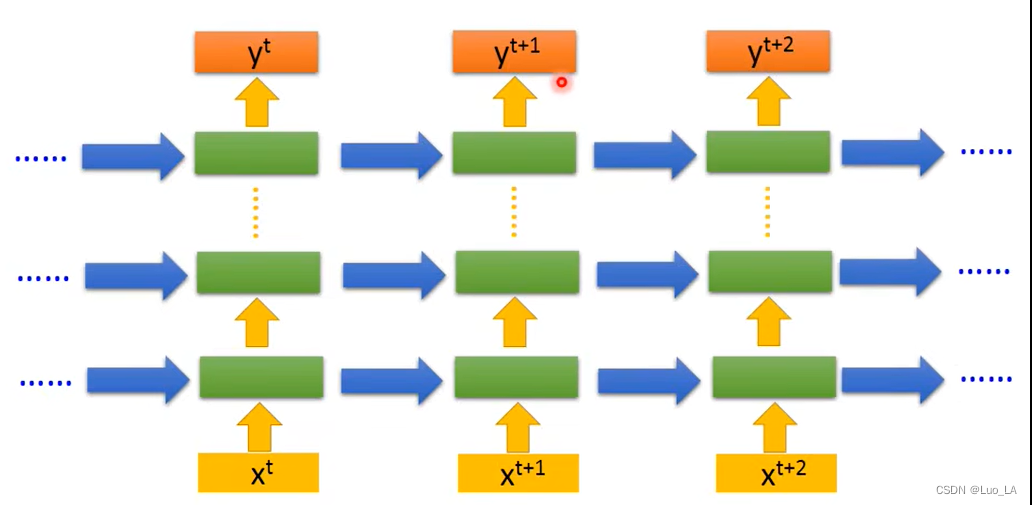
深层循环神经网络(DRNN)
解决更复杂的序列任务,可以把单层RNN叠起来或者输出前全连接结合使用。
普通RNN结构的缺陷
第一,前部序列信息在传递到后部的同时,信息权重下降,导致重要信息丢失。求解过程中梯度消失。

第二,RNN在训练过程中有时会出现参数丢失的情况。
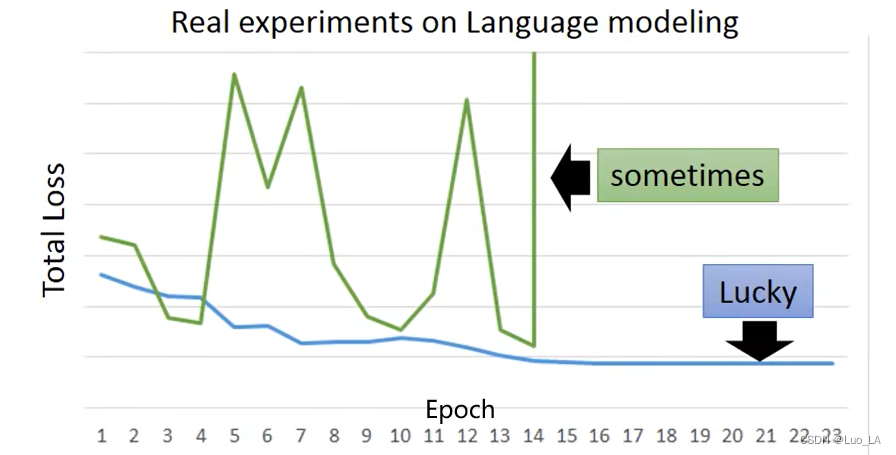
在最小化损失函数的过程中,会遇到梯度突然剧烈抖动的情况,从而导致参数丢失。
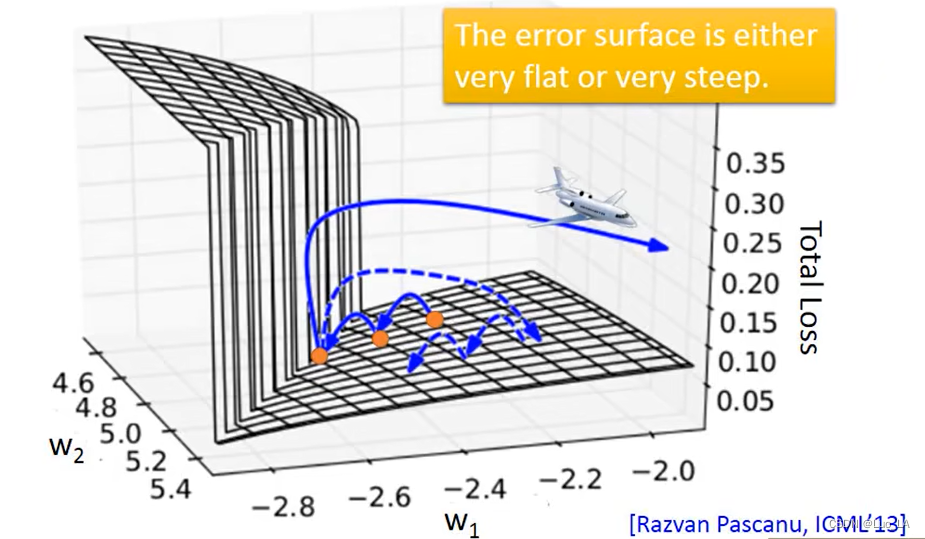
那么为什么会这样呢?
以下图的RNN结构为例,假设
W
i
,
W
o
W^i,W^o
Wi,Wo 都是1,输入长度为1000,那么
y
1000
=
w
999
y^{1000}=w^{999}
y1000=w999
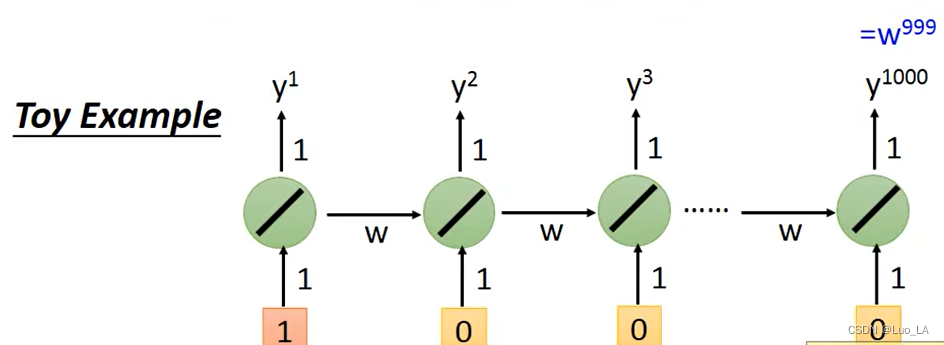
我们假设
w
w
w初值为1,在
w
w
w进行小幅度变化时,会发生什么情况呢?

所以 RNN 的问题就是它在训练过程中,同样的
w
w
w 在不同的时间点被反复使用,
w
w
w 一旦产生影响,都将会造成很大的影响。
长短期记忆网络 LSTM(Long Short-term Memory)
使用 LSTM 可以优化上面提到的 RNN 结构的缺陷。在原有的普通RNN结构单元上增加记忆细胞
c
i
c^i
ci ,可以传递前部远处部位信息。
LSTM结构由三个门,四个输入,一个输出组成。三个门分别是 input gate,forget gate,output gate。通过这三个门来控制哪些信息该遗忘丢弃,哪些信息该保留,或者保持不变。四个输入分别是,输入数据
Z
Z
Z,输入门控制信号
Z
i
Z_i
Zi ,忘记门控制信号
Z
f
Z_f
Zf和输出门控制信号
Z
o
Z_o
Zo。
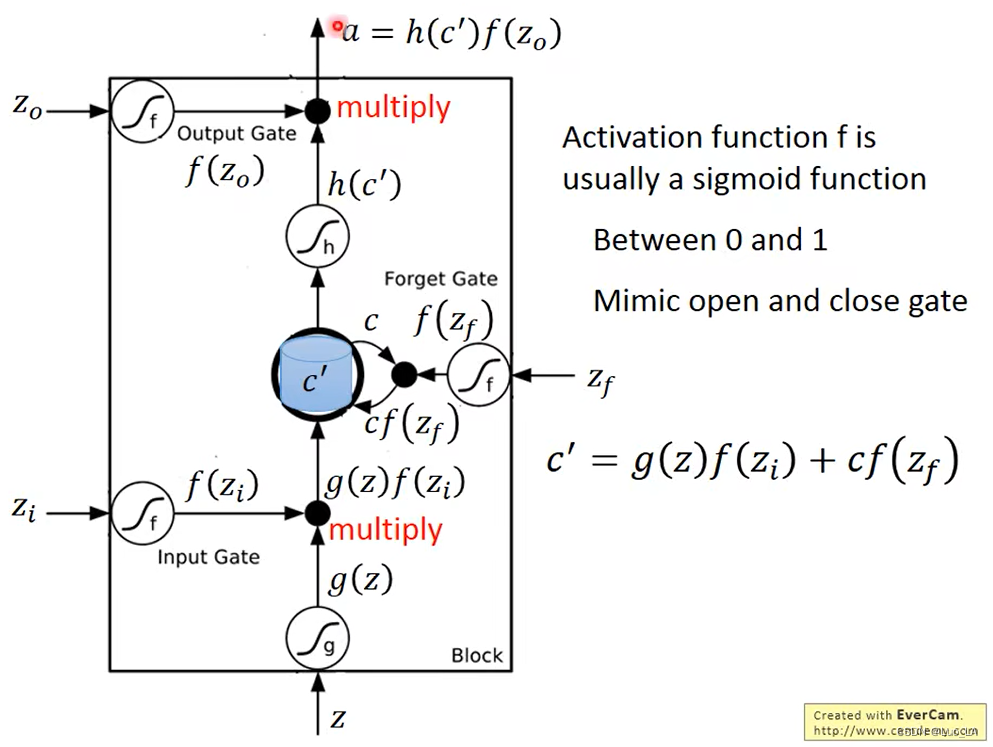
这里的门可以理解成为一个激活函数,这个激活函数通常是 sigmoid 函数,因为经过 sigmoid 函数的值在0和1之间,用来控制门的关闭和打开。
假设 memory 中原来存放的值为 c c c,更新之后的值为 c ′ = g ( z ) f ( z i ) + c f ( z f ) c'=g(z)f(z_i)+cf(z_f) c′=g(z)f(zi)+cf(zf), c ′ c' c′就是新的存放在 memory 中的值。从这个公式中我们可以看出, f ( z i ) f(z_i) f(zi) 就是控制 Z Z Z 可不可以输入的一道关卡, f ( z i ) = 0 f(z_i)=0 f(zi)=0 则没有输入, f ( z i ) = 1 f(z_i)=1 f(zi)=1 则有输入。 f ( z f ) f(z_f) f(zf) 控制memory中的值会不会更新。 f ( z f ) = 0 f(z_f)=0 f(zf)=0 时,忘记门开启,把0写进cell, f ( z f ) = 1 f(z_f)=1 f(zf)=1 时,直接通过,cell中值不变还是c。 f ( z o ) f(z_o) f(zo) 控制是否有输出的值。
Z
i
,
Z
f
,
Z
,
Z
o
Z_i,Z_f,Z_,Z_o
Zi,Zf,Z,Zo 都是由
X
X
X 乘上权重矩阵得到的输入。如下如所示进行序列输入。
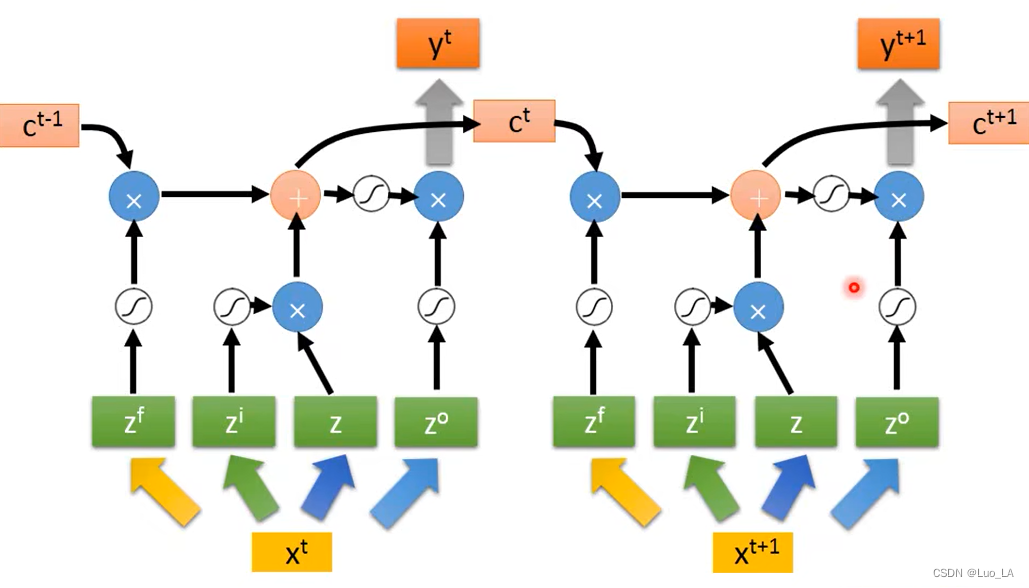
LSTM 可以解决 RNN 梯度消失的问题。RNN memory里面的值每一次都会被清空,而LSTM 里面的 memory 是一直被叠加的,除非忘记门被关闭的时候才会清空。