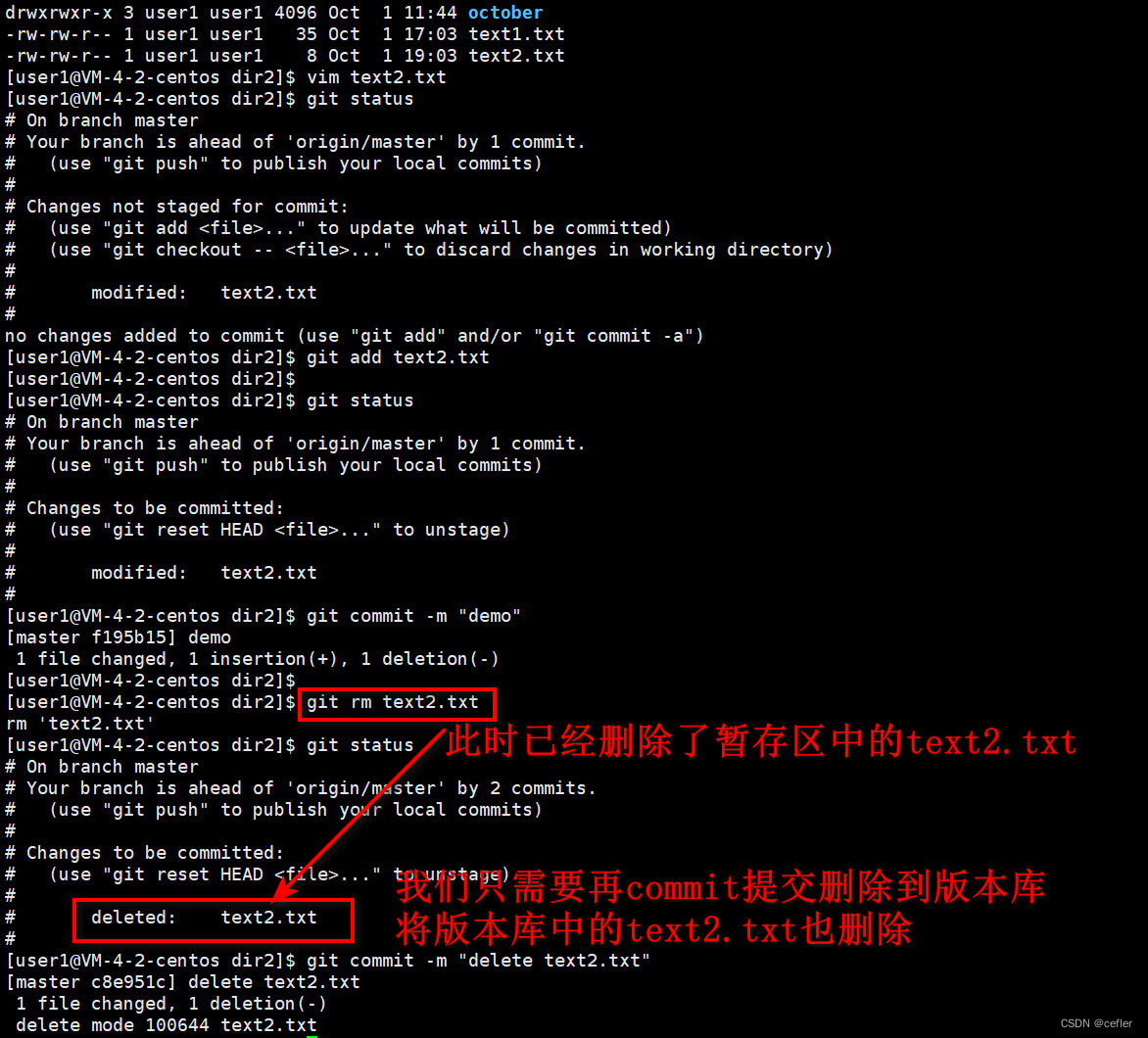
质数的判定：

质数：i>1，并且i的因子只有1和它本身。

思路：

对于n如果n%i==0那么n/i和i都是n的因子，对于n的每一对因子，至少有一个在1-,所以我们只需要判断1-是否有能整数n的数即可。时间复杂度o().

代码：

#define _CRT_SECURE_NO_WARNINGS 
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<unordered_map>
#include<map>
using namespace std;
#define LL  long long
const int N = 1e5+1000;
const long long  mod = 1e9 + 7;
#define  rep(i,a,b) for (int i = a; i <= b; i++) 
#define per(i, a, b) for(int  i=a;i>=b;i--)
int n,cnt;
int su[N], a[N],x,flag=0;
unordered_map<int, int> p;
int isprime(int x)
{
    if (x < 2) return 0;
    for (int i = 2; i <= x/ i; i++)
    {
        if (x % i == 0)
            return 0;    
    }
    return 1;
}
int main()
{
    
    cin >> n;
    while (n--)
    {
        cin >> x;
        if (isprime(x))
            cout << "Yes" << endl;
        else
            cout << "No" << endl;
    }
    return 0;
}

质因子分解： 

思路：

对于任意整数，他的质因子最多只有一个落在-n中间，所以我们可以先求1-的质因子，如果n>1，再输出n即可。

#define _CRT_SECURE_NO_WARNINGS 
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<unordered_map>
#include<map>
using namespace std;
#define LL  long long
const int N = 1e5+1000;
const long long  mod = 1e9 + 7;
#define  rep(i,a,b) for (int i = a; i <= b; i++) 
#define per(i, a, b) for(int  i=a;i>=b;i--)
int n,cnt;
int su[N], a[N],x,flag=0;
unordered_map<int, int> p;
void into()
{
    a[0] = a[1] = 1;
    rep(i, 1, N)
    {
        if (a[i]) continue;
        su[++cnt] = i;
        p[i] = 1;
        for (int j = 2 * i; j <= N; j += i)
            a[j] = 1;
    }
}
int main()
{
    into();
    cin >> n;
    while (n--)
    {
        cin >> x;
        int i = 2,cn=0,t=x;
        while (x>1&&i<=t/i)
        {
            while (x % i == 0)
                cn++, x /=i;
            if (cn != 0)
                cout << i << " " << cn << endl;
            i++;
            cn = 0;
        }
        if (x > 1)
            cout << x << " " << 1 << endl;
        cout << endl;
    }
    return 0;
}