算法通关手册 刷题笔记1 数组基础

持续更新中

数组操作题目

题号	标题	题解	标签	难度
0189	轮转数组	Python	数组	中等
0066	加一	Python	数组	简单
0724	寻找数组的中心下标	Python	数组	简单
0485	最大连续 1 的个数	Python	数组	简单
0238	除自身以外数组的乘积	Python	数组	中等

0189 轮转数组

AC

自己的解法

• 一开始犯了错误：注意python中数组的赋值

  • 两个列表list1和list2，直接用等号赋值，list2修改后，list1也会被修改
    

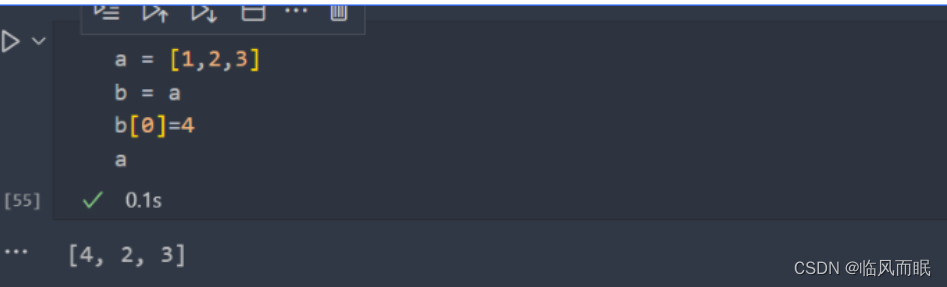
    • 想要不改变原列表，使用[:]或者.copy()

  • 参考:python把一个数组赋值给另一个数组

  • 一开始的错误代码

    def rotate2( nums, k):
            """
            :type nums: List[int]
            :type k: int
            :rtype: None Do not return anything, modify nums in-place instead.
            """
            nums2 = nums
            for i in range(len(nums)):
                nums2[i] =  nums[(i+k+1)%len(nums)]
    
            return nums2
    rotate2([1,2,3,4,5,6,7],3)
    

    [5, 6, 7, 5, 6, 7, 5]
    

    来分析一下： nums2[0] = nums[4] , 这时候 nums2[0]和nums[0]都变成了5 ,所以nums2[3] = nums[0] = 5…

• 改了改，以为自己做对了，但是没AC

  def rotate(nums, k):
          """
          :type nums: List[int]
          :type k: int
          :rtype: None Do not return anything, modify nums in-place instead.
          """
          # nums2 = num
          nums2 = []
          for i in range(len(nums)):
              nums2.append(0)
          for i in range(len(nums)):
          #下面这俩应该都可以
  **            nums2[i] = nums[(i+k+1) % len(nums)]
              # nums2[(i+k)%len(nums)] =  nums[i]**
          return nums2
  rotate([1,2,3,4,5,6,7],3)
  

  [5, 6, 7, 1, 2, 3, 4]    
  

  难绷，审题！ 去掉return就行了

  

其他解法

• 算法通关手册上的python解法

  class Solution:
      def rotate(self, nums: List[int], k: int) -> None:
          """
          Do not return anything, modify nums in-place instead.
          """
          n = len(nums)
          k = k % n
          self.reverse(nums, 0, n-1)
          self.reverse(nums, 0, k-1)
          self.reverse(nums, k, n-1)
      
      def reverse(self, nums: List[int], left: int , right: int) -> None:
          while left < right:
              tmp = nums[left]
              nums[left] = nums[right]
              nums[right] = tmp
              left += 1
              right -=1
  

• 力扣题解区上面看到切片的解法，感觉very smart

  class Solution:
      def rotate(self, nums: List[int], k: int) -> None:
          """
          Do not return anything, modify nums in-place instead.
          """
          k = k % len(nums)
          nums[:] = nums[-k:] + nums[:-k]
  

知识点查漏补缺

关于python中的数组赋值

• https://www.geeksforgeeks.org/array-copying-in-python/
• https://www.runoob.com/w3cnote/python-understanding-dict-copy-shallow-or-deep.html

python中对象的引用

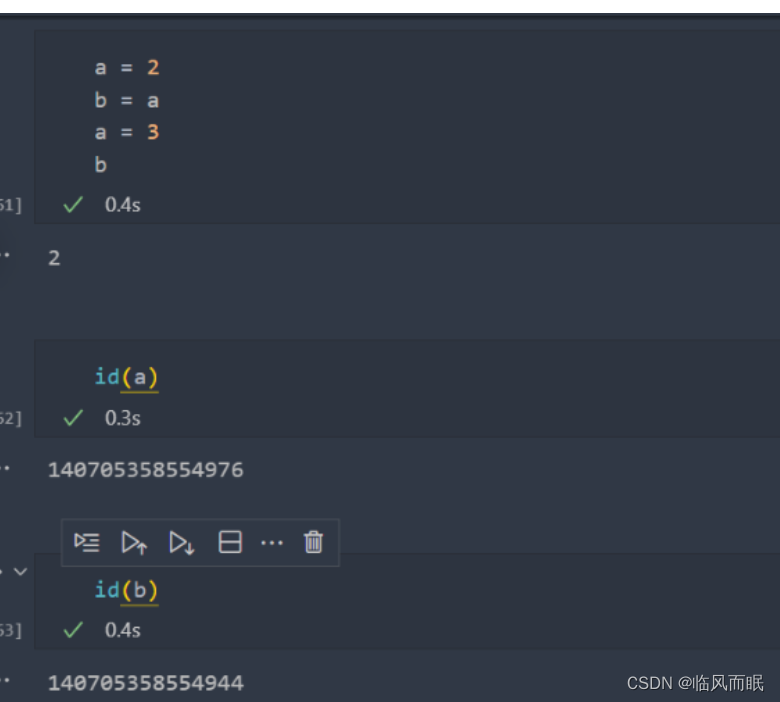
• 试了下整数变量会不会和那个数组也是一样的情况，不是的

  

• 于是去查了查

  

  • Python可变对象和不可变对象

0066 加一

AC

自己的解法

• 一开始写的代码

  class Solution:
      def plusOne(self, digits: List[int]) -> List[int]:
          k = len(digits)
          sum = 0
          m = 1
          while k >= 1:
              sum += m*digits[k-1]
              m *= 10
              k -= 1
          newlis = []
          sum += 1
          j = 0
          while sum > 0:
  
              # newlis.append(sum % 10)
              newlis.insert(j, sum % 10)
              sum //=10
          return newlis
  

其他解法

• 看《算法通关手册》的题解

  • 感觉思路很清晰

    有可能有进位，先在前面放个0，末位加个1，啥时候会有进位呢，那个位置上的数字为10的时候，如果低位都没碰到10，那么高位肯定不会碰到10，直接break，返回原来的列表，即现在的digits[1:]

    哪一位有进位，就把那一位变成0，然后它的前一位+1

    如果会一直进位到最高位，那么就返回digits

    

    def plusOne(self, digits: List[int]) -> List[int]:
        digits = [0] + digits
        digits[len(digits)-1] += 1
        for i in range(len(digits)-1,0,-1):
            if digits[i] != 10:
                break
            else:
                digits[i] = 0
                digits[i-1] += 1
            
        if digits[0] == 0:
            return digits[1:] 
        else:
            return digits
    

  • 注意 [0] + digits的顺序是有影响的

    

• 力扣官方题解 妙啊

  • 思路

    • 找出最长的后缀9
      • 如果 $\textit{digits} $的末尾没有 999，例如 [1,2,3]，那么我们直接将末尾的数加一，得到 [1, 2, 4]并返回；
      • 如果 $\text{digits}$ 的末尾有若干个 9，例如 [1,2,3,9,9]那么我们只需要找出从末尾开始的第一个不为 999的元素，即 333，将该元素加一，得到 [1,2,4,9,9]]。随后将末尾的 999 全部置零，得到 [1,2,4,0,0]并返回。
      • 如果 $\text{digits}$ 的所有元素都是 999，例如 [9,9,9,9,9]，那么答案为$[1,0,0,0,0,0]$。我们只需要构造一个长度比 $\text{digits}$多 111 的新数组，将首元素置为 111，其余元素置为 000 即可。

  • 算法

    • 只需要对数组$\text{digits}$进行一次逆序遍历，找出第一个不为 999 的元素，将其加一并将后续所有元素置零即可。如果 $\text{digits}$中所有的元素均为 999，那么对应着「思路」部分的第三种情况，我们需要返回一个新的数组。

      class Solution:
          def plusOne(self, digits: List[int]) -> List[int]:
              n = len(digits)
              for i in range(n -1, -1, -1):
                  if digits[i] != 9:
                      digits[i] += 1
                      for j in range(i + 1, n):
                          digits[j] = 0
                      return digits
      
              return [1] + [0] * n
      

知识点查漏补缺

• 在前面自己的解法那个代码里面

  • 放到vscode里面会有这个问题

    

    • 需要from typing import List

  • 那一步用append顺序会反 双边队列里面才有appendleft

    • 用insert比较好

    • 另外别记混了 那个appendleft是双边队列才有的 之前在头歌学过👇

    • ​ 2-4 Python入门之collections模块

    • 不过这题确实可以试试双边队列

      • ​ Deque in Python - GeeksforGeeks

  • python里面的//和/ 两种除法的区别

    

    • //是向下取整

0724 寻找数组的中心下标

AC

自己的解法

• 一开始的错误代码

      - 一开始的代码
  class Solution:
      def pivotIndex(self, nums: List[int]) -> int:
          suml = 0 # 从左往右的和
          sumr = 0 # 从右往左的和
          # l = len(nums)
          lisl = []
          lisr = []
          for i in range(len(nums)):
              suml += nums[i]
              lisl.append(suml)
          for i in range(len(nums)-1,-1,-1):
              sumr += nums[i]
              lisr.append(sumr)   
          # flag = 0
          if lisl[0] == lisl[len(nums)-1]:
              return 0
          elif lisr[0] == lisr[len(nums)-1]:
              return len(nums)-1
          else:
              for j in range(len(nums)):
                  
                  if lisl[j] == lisr[j]:
                      return j
      
          return -1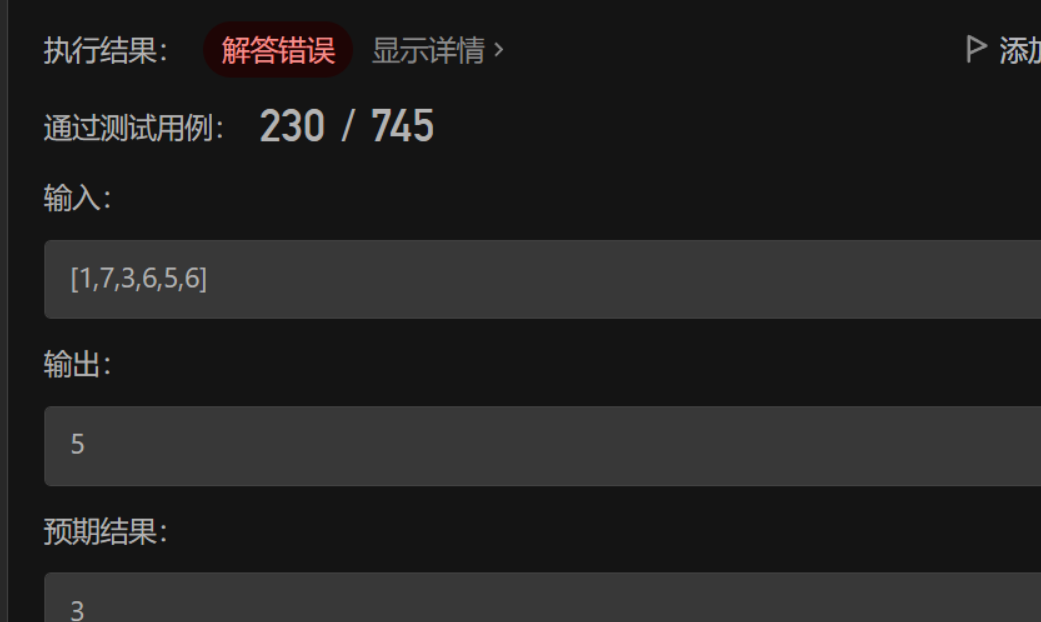   
  

  

  lisl=[1,8,11,17,22,28]

  lisr=[6,11,17,20,21,28]

  返回5是不正确的，突然发现自己这个代码只适合中心点两边元素个数相等的情况…

  按照那个思路，在左和数组and 右和数组相同位置的话，那只能是元素个数相同了

• 改了改，还是有问题

  class Solution:
      def pivotIndex(self, nums: List[int]) -> int:
          suml = 0 # 从左往右的和
          sumr = 0 # 从右往左的和
          # l = len(nums)
          lisl = []
          lisr = []
          for i in range(len(nums)):
              suml += nums[i]
              lisl.append(suml)
          for i in range(len(nums)-1,-1,-1):
              sumr += nums[i]
              lisr.append(sumr)   
          # flag = 0
          if lisl[0] == lisl[len(nums)-1]:
              return 0
          elif lisr[0] == lisr[len(nums)-1]:
              return len(nums)-1
          else:
              for j in range(len(nums)):
                  if lisl[j] == lisr[len(nums)-1-j]:
                      return j
  
      
          return -1   
  

  

  一开始感觉自己把两种特殊情况提出来很聪明，结果发现好像题目中这个条件的限制

  如果数组有多个中心下标，应该返回 最靠近左边 的那一个

  那么当左边的和为0的话，右边如果很多0，就会返回最右边的0

• AC了

  • 总结一下自己的思路

    • 设立一个数组，每一位依次存储原数组nums从左到右的和

  • 再设立一个数组，每一位一次存储原数组nums从右到左的和

    • 然后由于题目要求返回靠左的中心点，那下标就从0到 len(nums)-1 从小到大遍历

  • 遇到相等的就返回j

• 代码如下

  class Solution:
      def pivotIndex(self, nums: List[int]) -> int:
          suml = 0 # 从左往右的和
          sumr = 0 # 从右往左的和
          # l = len(nums)
          lisl = []
          lisr = []
          for i in range(len(nums)):
              suml += nums[i]
              lisl.append(suml)
          for i in range(len(nums)-1,-1,-1):
              sumr += nums[i]
  
          for j in range(len(nums)):
                  if lisl[j] == lisr[len(nums)-1-j]:
                      return j
  
      
          return -1   
  

  ​ 但时空复杂度大了些

  

其他做法

• 官方题解：前缀和

  • 思路
    • 记数组的和为$total$,当遍历到第$i$个元素时，左侧元素之和为$sum$,那么右侧元素的和为$total-num{s}_i-sum$,左右侧元素相等即为$sum=total-num{s}_i-sum$，即$2\times sum+num{s}_i=total$
    • 当中心索引左侧或右侧没有元素时，即为零个项相加，这在数学上称作「空和」（$\text{empty sum}$）。在程序设计中我们约定「空和是零」

• 题解没给python的，自己AC

  • 对着题解的文字解释，自己写了一个…但是不全对

    class Solution:
        def pivotIndex(self, nums: List[int]) -> int:
            total = 0
            sum = 0
            for i in range(len(nums)):
                total += nums[i]
            for i in range(1,len(nums)):
                sum +=nums[i-1]
                if 2*sum + nums[i] == total:
                        return i
                # if i != len(nums)-1:
                #     if 2*sum + nums[i+1] == total:
                #         return i-1
                
            return -1
    

    

    ​ 代码的问题在于下面的循环的i是从1开始遍历

  • 改了个离谱的

    class Solution:
        def pivotIndex(self, nums: List[int]) -> int:
            total = 0
            sum = 0
            for i in range(len(nums)):
                total += nums[i]
            for i in range(len(nums)):
                sum +=nums[i]
                if i != len(nums)-1:
                    if 2*sum + nums[i+1] == total:
                        return i+1
                    return len(nums) - 1
            return -1
    

  • AC了

    ​ 既然一开始写的漏了0的情况，那就单独考虑嘛

    ​ 这样会是啥情况，除了第一个元素，右边的和为0，那么列表的和肯定等于第一个元素

    class Solution:
        def pivotIndex(self, nums: List[int]) -> int:
            total = 0
            sum = 0
            for i in range(len(nums)):
                total += nums[i]
            if total == nums[0]:
                return 0
            for i in range(1,len(nums)):
                sum +=nums[i-1]
                if 2*sum + nums[i] == total:
                        return i
    
                
            return -1
    

• 算法通关手册题解

  • 只要改一下我的AC写法一点点就行，就是我是从下标1开始遍历，只要改一处代码的位置，就可以从0开始遍历，无需单独处理

    class Solution:
        def pivotIndex(self, nums: List[int]) -> int:
            total = 0
            sum = 0
            for i in range(len(nums)):
                total += nums[i]
            if total == nums[0]:
                return 0
            for i in range(len(nums)):
                
                if 2*sum + nums[i] == total:
                        return i
                sum +=nums[i]
                
            return -1
    

0485 最大连续1的个数

AC

• 刚开始的思路

  • 想到了奇偶校验码😂

  • 想到了看成连续的数字，110111：十一万零一百一十一

  • 记录0的位置，然后逐个计算0之间的距离，选出最大的，同时 ，数组的第一个元素的前一个元素记为-1以及最后一个元素的后一个记为len(nums)

    • 把这些0所在的位置存在一个数组里面，然后计算每两个之间的差，把这些差存入数组，然后选出里面最大的

    • 初始数组[-1]

    • 遍历的时候一直append 0的下标

    • 最后再append len(nums)

    • 突然发现这样子还不如直接统计1的位置…

    • 因为可能出现连续的0… 而不是说0全是分开的…

    • 下面这个感觉用处不大

      class Solution:
          def findMaxConsecutiveOnes(self, nums: List[int]) -> int:
              maxLen = len(nums)
              # zeroNums = [-1,maxLen]
              zeorNums = [-1]
              for  i in range(len(nums)):
                  if nums[i]==0:
                      zeroNums.append(i)
              
              zeroNums.append(maxLen)
              
    

  • 记录1的位置

  • 思考了十分钟…看答案吧…

• 官方题解思路

  • 一次遍历
    • 记录两个数：当前连续的1的个数和最大的连续的1的个数
      • 一开始两个量都是0
      • 当遇到第一个1的时候，当前连续的1的个数加1，后面遇到1，当前连续的1的个数就加1，遇到0，就把当前连续的1的个数置为0，同时更新最大的连续的1的个数
        • 更新指：比较这一次的连续的1的个数和之前记录的最大的连续的1的个数，取最大值
    • 遍历数组结束之后，需要再更新（比较）一次，因为数组的最后一个元素可能是1，且最长连续1的子数组可能出现在数组的末尾
    • 复杂度分析
      • 时间复杂度：O(n)，其中n为数组的长度
      • 空间复杂度：O(1)

• 看完思路自己写一遍

  class Solution:
      def findMaxConsecutiveOnes(self, nums: List[int]) -> int:
          maxCount = count = 0
          
          for i in range(len(nums)):
              if nums[i] == 1:
                  count += 1
              else:
                  maxCount = max(maxCount,count) 
                  count = 0
          maxCount = max(maxCount,count)
          
          return maxCount
          
  

• 力扣官方题解代码

  class Solution:
      def findMaxConsecutiveOnes(self, nums: List[int]) -> int:
          maxCount = count = 0
  
          for i, num in enumerate(nums):
              if num == 1:
                  count += 1
              else:
                  maxCount = max(maxCount, count)
                  count = 0
          
          maxCount = max(maxCount, count)
          return maxCount
  
  

知识点查漏补缺

enumerate

• https://www.runoob.com/python3/python3-func-enumerate.html

• 描述

  • enumerate() 函数用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列，同时列出数据和数据下标，一般用在 for 循环当中

• 语法

  • enumerate(sequence, [start=0])
    

• 参数

  • sequence – 一个序列、迭代器或其他支持迭代的对象
  • start – 下标起始位置

• 返回值

  • 返回enumerate（枚举）对象

• 实例

  • seasons = ['Spring', 'Summer', 'Fall', 'Winter']
    list(enumerate(seasons)) [(0, 'Spring'), (1, 'Summer'), (2, 'Fall'), (3, 'Winter')]
    list(enumerate(seasons, start=1)) # 小标从 1 开始 
    [(1, 'Spring'), (2, 'Summer'), (3, 'Fall'), (4, 'Winter')]
    

0238 除自身以外数组的乘积

AC

• 刚开始思路 暴力解法

  • 哈哈哈，如果没说 请不要使用除法 ， 我感觉我一开始还想不到这个方法

  • 无脑求解

  • class Solution:
        def productExceptSelf(self, nums: List[int]) -> List[int]:
            answer = []
            l = len(nums)
            for i in range(l):
                ans = 1
                for k in range(l):
                    if k != i:
                        ans *= nums[k]
                answer.append(ans)
        
            return answer
                    
    

  • 简单的可以，但是复杂的时间复杂度会爆

  

• 直接看题解… 摆烂

  • 方法一：左右乘积列表

    • 利用索引左侧所有数字的乘积和右侧所有数字的乘积（即前缀与后缀）相乘得到答案

    • 算法描述

      • 初始化俩空数组L和R。对于给定的索引i，L[i]代表i左侧所有数字的乘积,R[i]代表i右侧所有数字的乘积

      • 用两个循环来填充L和R数组的值

        • 对于数组L，L[0]应该是1，因为第一个元素的左边没有元素。对于其他元素：L[i] = L[i-1] * nums[i-1]
        • 对于数组R，R[length-1] 应为 1。length 指的是输入数组的大小。其他元素：R[i] = R[i+1] * nums[i+1]

      • 当 R 和 L 数组填充完成，我们只需要在输入数组上迭代，且索引 i 处的值为：L[i] * R[i]

    • 代码

      class Solution:
          def productExceptSelf(self, nums: List[int]) -> List[int]:
              length = len(nums)
              
              # L 和 R 分别表示左右两侧的乘积列表
              L, R, answer = [0]*length, [0]*length, [0]*length
              
              # L[i] 为索引 i 左侧所有元素的乘积
              # 对于索引为 '0' 的元素，因为左侧没有元素，所以 L[0] = 1
              L[0] = 1
              for i in range(1, length):
                  L[i] = nums[i - 1] * L[i - 1]
              
              # R[i] 为索引 i 右侧所有元素的乘积
              # 对于索引为 'length-1' 的元素，因为右侧没有元素，所以 R[length-1] = 1
              R[length - 1] = 1
              for i in reversed(range(length - 1)):
                  R[i] = nums[i + 1] * R[i + 1]
      
              # 对于索引 i，除 nums[i] 之外其余各元素的乘积就是左侧所有元素的乘积乘以右侧所有元素的乘积
              for i in range(length):
                  answer[i] = L[i] * R[i]
              
              return answer
      
      

    • 复杂度分析

      • 时间复杂度：O(N)，其中 N 指的是数组 nums 的大小。预处理 L 和 R 数组以及最后的遍历计算都是 O(N) 的时间复杂度。
      • 空间复杂度：O(N)，其中 N 指的是数组 nums 的大小。使用了 L 和 R 数组去构造答案，L 和 R 数组的长度为数组 nums 的大小。

• 方法二：空间复杂度为O(1)的方法

  

  • 算法描述

    • 初始化 answer 数组，对于给定索引 i，answer[i] 代表的是 i 左侧所有数字的乘积。
    • 构造方式与之前相同，只是我们试图节省空间，先把 answer 作为方法一的 L 数组。
    • 这种方法的唯一变化就是我们没有构造 R 数组。而是用一个遍历来跟踪右边元素的乘积。并更新数组 answer[i]=answer[i]R。然后 R更新为 R=Rnums[i]，其中变量 R表示的就是索引右侧数字的乘积。

  • 代码

    class Solution:
        def productExceptSelf(self, nums: List[int]) -> List[int]:
            length = len(nums)
            answer = [0]*length
            
            # answer[i] 表示索引 i 左侧所有元素的乘积
            # 因为索引为 '0' 的元素左侧没有元素， 所以 answer[0] = 1
            answer[0] = 1
            for i in range(1, length):
                answer[i] = nums[i - 1] * answer[i - 1]
            
            # R 为右侧所有元素的乘积
            # 刚开始右边没有元素，所以 R = 1
            R = 1;
            for i in reversed(range(length)):
                # 对于索引 i，左边的乘积为 answer[i]，右边的乘积为 R
                answer[i] = answer[i] * R
                # R 需要包含右边所有的乘积，所以计算下一个结果时需要将当前值乘到 R 上
                R *= nums[i]
            
            return answer
    

python reversed

二维数组题目

题号	标题	题解	标签	难度
0498	对角线遍历	Python	数组、矩阵、模拟	中等
0048	旋转图像	Python	数组	中等
0073	矩阵置零	Python	数组	中等
0054	螺旋矩阵	Python	数组	中等
0059	螺旋矩阵 II	Python	数组、矩阵、模拟	中等
0289	生命游戏	Python	数组、矩阵、模拟	中等

参考资料

• 算法通关手册在线开源书