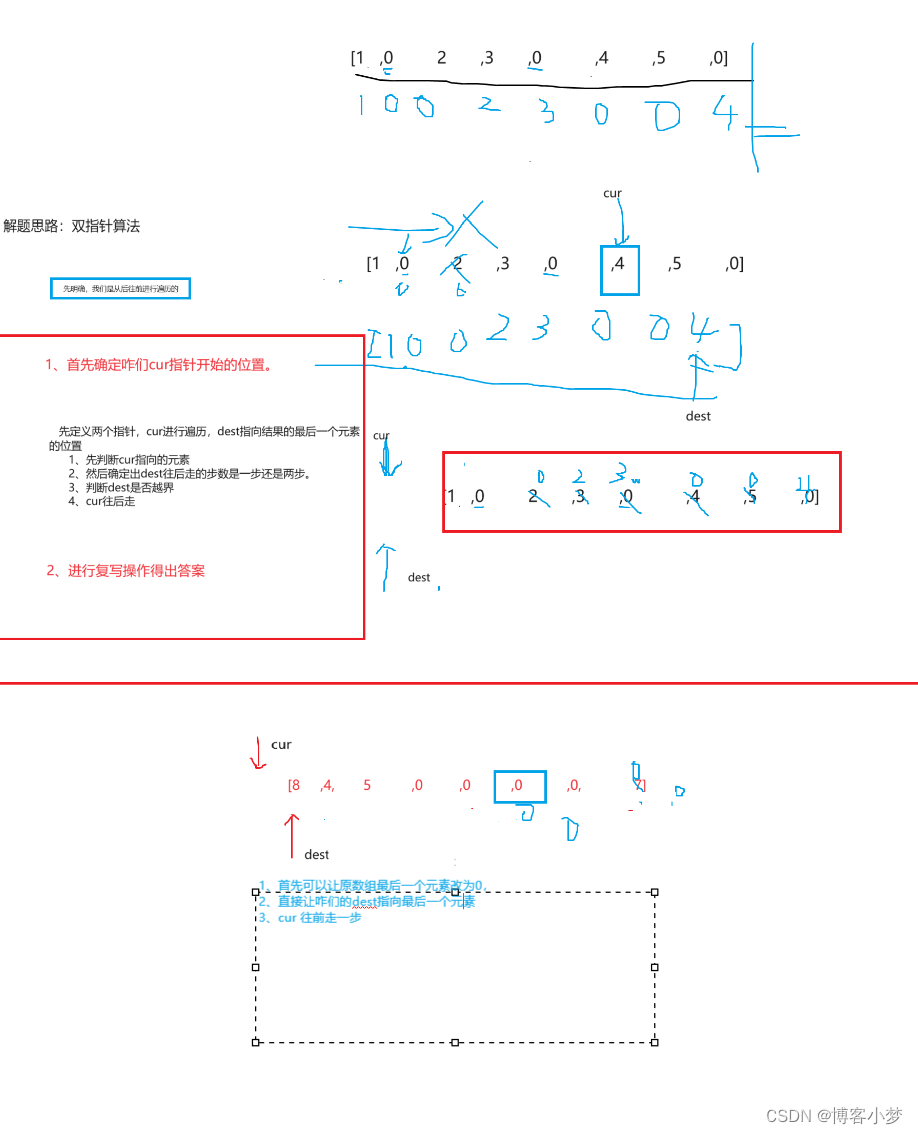
本文还是来源于http://t.csdnimg.cn/P5zOD,但肯定不可能只有这些内容,否则那位作者应该会打我……,在这里,只是讲解优化类问题比较常用的方法,以TSP问题为例,适合入门。
模拟退火
模拟退火是一种概率算法,它从某个解出发,随机产生下一个解,并根据一定的准则来接受或拒绝新解,同时随着迭代的进行逐渐降低“温度”。
基础示例
%% 模拟退火
clc,clear
% 模拟退火(求最小)。模拟退火是一种概率算法,它从某个解出发,随机产生下一个解
% 并根据一定的准则来接受或拒绝新解,同时随着迭代的进行逐渐降低“温度”。
temperature = 100; % 初始温度,开始时较高以接受更多的解。
final_temperature = 1; % 算法停止的最低温度。
time_temperature = 1; % 用来计算当前温度下已经迭代了多少步,作用类似于计数器。
time_tuihuo = 10; % 退火步长,是每个温度下的迭代步数。
cooling_rate = 0.95; % 是每次降温的比率。
% 初始化随机数生成器,以使结果具备可重复性
% rng(0,'twister');
% 生成范围a-b的随机数
a = -10; b = 10;
% rang_math = (b-a).*rand(1000,1) + a;是初始解。
rang_math = (b-a).*rand + a;
% 定义函数,求最小值
f = @(x)(x.^4 + 4.*x.^3 - x.^2);
current_old = f(rang_math);
while final_temperature < temperature
rang_math = (b-a).*rand + a; % 随机数
current_new = f(rang_math); % 生成新解
diff = current_new - current_old; %diff 是新旧解的差值。
% 使用 Metropolis 准则来决定是否接受新解。
%如果新解比旧解好(即 diff<0)或者满足一定的概率(rand < exp(-diff/(temperature))),则接受新解。
if(diff<0)||(rand < exp(-diff/(temperature)))
route = rang_math;
current_old = current_new;
time_temperature = time_temperature + 1;
end
% 当在一个温度下迭代了 time_tuihuo 步之后,降低温度 (temperature = temperature * cooling_rate)。
if time_temperature == time_tuihuo
temperature = temperature * cooling_rate;
time_temperature = 0;
end
end
plot([a:b],f([a:b])); % 原函数图像
hold on;
plot(route,current_old,'ko', 'linewidth', 2); % 作解的图像这段代码是使用模拟退火算法来找到一个函数的最小值。其中,基础部分涉及到匿名函数:
在 MATLAB 中,当你创建一个匿名函数时,你必须使用
.进行点乘或点除等运算,以确保每个元素都被单独操作。而且你应该使用.*、./和.^而不是*,/, 和^。此外,您应该避免使用未定义的变量和符号。下面是你给出的函数的一些可能的正确形式。
1.使用 .* 和 .^ 进行点乘和点幂运算:
f = @(x)(x.^4 + 4.*x.^3 - x.^2);2.如果你想进行标量操作(而不是数组操作),你可以直接使用 * 和 ^,但这种情况下 x 只能是一个标量,而不是一个数组:
f = @(x)(x^4 + 4*x^3 - x^2);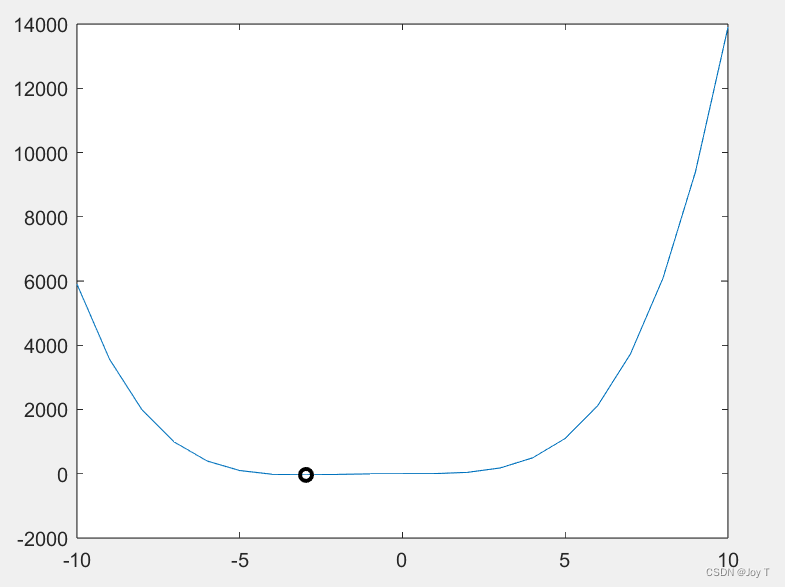
上图结果表明找到了函数的近似最小值,不一定是全局最优解哦,只能说比较接近。优化类方法都是这样,都是满足结果在一个正确合理的范围就行。
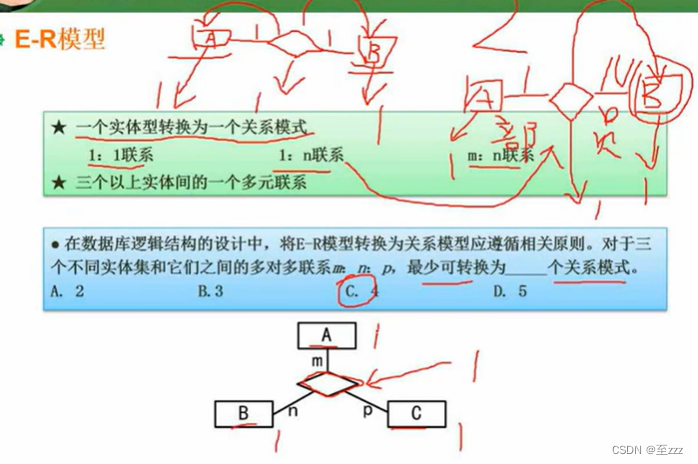
模拟退火求解TSP问题
% 实际操作
citys = [
1304 2312;
3639 1315;
4177 2244;
3712 1399;
3488 1535;
3326 1556;
3238 1229;
4196 1004;
4312 790;
4386 570;
3007 1970;
2562 1756;
2788 1491;
2381 1676;
1332 695;
3715 1678;
3918 2179;
4061 2370;
3780 2212;
3676 2578;
4029 2838;
4263 2931;
3429 1908;
3507 2367;
3394 2643;
3439 3201;
2935 3240;
3140 3550;
2545 2357;
2778 2826;
2370 2975;
];
save('citys_data.mat', 'citys');% 使用 save 命令将数据保存为 .mat 文件:
% 导入数据
load citys_data.mat
% 初始化参数
temperature = 1000;
final_temperature = 1;
cooling_rate = 0.995;
time_temperature = 1;
time_tuihuo = 100;
% 初始化路径
route = 1:31;
current_dist = total_distance(route, citys);
% 存储每次迭代的距离
distances = [];
while temperature > final_temperature
for i = 1:time_tuihuo
% 随机交换两个城市的位置来产生新的路径
new_route = swapCities(route);
new_dist = total_distance(new_route, citys);
diff = new_dist - current_dist;
% 使用 Metropolis 准则来决定是否接受新路径
if (diff < 0) || (rand < exp(-diff / temperature))
route = new_route;
current_dist = new_dist;
time_temperature = time_temperature + 1;
end
end
% 存储当前的总距离
distances = [distances, current_dist];
% 降温
temperature = temperature * cooling_rate;
end
% 输出最终结果
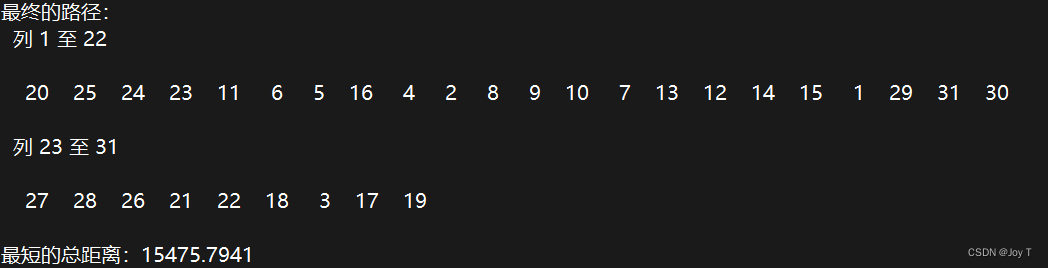
disp('最终的路径:');
disp(route);
fprintf('最短的总距离:%.4f\n', current_dist);
% 绘制最终路径
figure;
plot(citys(:,1), citys(:,2), 'o'); % 绘制城市
hold on;
% 绘制路径
for i = 1:(length(route)-1)
plot([citys(route(i), 1), citys(route(i+1), 1)], ...
[citys(route(i), 2), citys(route(i+1), 2)], 'k-');
end
% 绘制从最后一个城市到第一个城市的路径
plot([citys(route(end), 1), citys(route(1), 1)], ...
[citys(route(end), 2), citys(route(1), 2)], 'k-');
hold off;
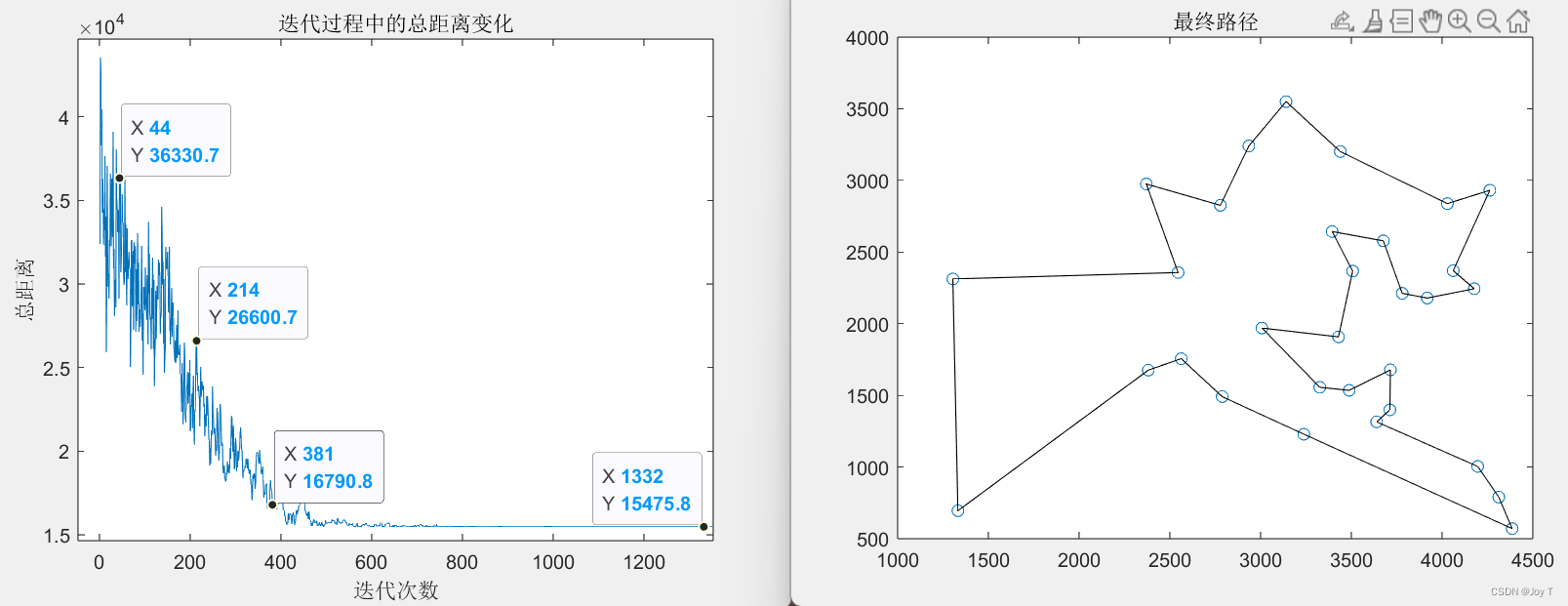
title('最终路径');
% 绘制迭代曲线图
figure;
plot(distances);
title('迭代过程中的总距离变化');
xlabel('迭代次数');
ylabel('总距离');
%下面是两个函数,注意一定要重新创建函数文件啊!
% 计算总距离的函数
function dist = total_distance(route, citys)
dist = 0;
for i = 1:(length(route)-1)
dist = dist + sqrt(sum((citys(route(i),:) - citys(route(i+1),:)).^2));
end
dist = dist + sqrt(sum((citys(route(end),:) - citys(route(1),:)).^2));
end
% 随机交换两个城市的位置的函数
function new_route = swapCities(route)
idx = randperm(length(route), 2);
new_route = route;
new_route(idx(1)) = route(idx(2));
new_route(idx(2)) = route(idx(1));
end结果:
蚁群算法
蚁群算法简介
蚁群算法 (Ant Colony Optimization, ACO) 是一种启发式搜索算法,灵感来源于现实世界中蚁群的觅食行为。在自然界中,蚂蚁通过释放一种称为信息素的化学物质来找到食物源,并通过这些信息素的浓度来引导其他蚂蚁。该算法模拟了这种行为。
蚁群算法和模拟退火的区别
基本原理:
- 蚁群算法是通过模拟蚂蚁寻找食物的行为来找到最优路径。
- 模拟退火是通过不断地在当前解的邻域中随机选取新的解,再根据某种准则来决定是否接受这个新解。
搜索策略:
- 蚁群算法利用多个搜索点(蚂蚁)同时进行搜索,并通过信息素来交流信息。
- 模拟退火通常从一个解开始,并在每个步骤中进行小的随机改变。
信息传递:
- 蚁群算法中,蚂蚁通过信息素进行信息交流。
- 模拟退火则没有这种信息交流机制。
适用问题:
- 蚁群算法主要用于解决组合优化问题,如TSP。
- 模拟退火可以应用于广泛的优化问题,包括组合优化和连续优化问题。
蚁群算法求解TSP
在应用蚁群算法求解TSP(旅行商问题)时,每一只蚂蚁都代表一种可能的路径。蚂蚁在路径上释放信息素,而后续的蚂蚁根据信息素的浓度来选择路径。最终信息素浓度最高的路径被认为是最优路径。
%% 蚁群算法求解TSP问题
% 计算城市间相互距离
n = size(citys,1);
D = zeros(n,n);
for i = 1:n
for j = 1:n
if i ~= j
D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));
else
D(i,j) = 1e-4;
end
end
end
% 初始化参数
m = 80; % 蚂蚁数量
alpha = 1; % 信息素重要程度因子
beta = 5; % 启发函数重要程度因子
rho = 0.1; % 信息素挥发因子
Q = 1; % 常系数
Eta = 1./D; % 启发函数
Tau = ones(n,n); % 信息素矩阵
Table = zeros(m,n); % 路径记录表
iter = 1; % 迭代次数初值
iter_max = 200; % 最大迭代次数
Route_best = zeros(iter_max,n); % 各代最佳路径
Length_best = zeros(iter_max,1); % 各代最佳路径的长度
Length_ave = zeros(iter_max,1); % 各代路径的平均长度
% 迭代寻找最佳路径
while iter <= iter_max
% 随机产生各个蚂蚁的起点城市
start = zeros(m,1);
for i = 1:m
temp = randperm(n);
start(i) = temp(1);
end
Table(:,1) = start;
% 构建解空间
citys_index = 1:n;
% 逐个蚂蚁路径选择
for i = 1:m
% 逐个城市路径选择
for j = 2:n
tabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表)
allow_index = ~ismember(citys_index,tabu);
allow = citys_index(allow_index); % 待访问的城市集合
P = allow;
% 计算城市间转移概率
for k = 1:length(allow)
P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta;
end
P = P/sum(P);
% 轮盘赌法选择下一个访问城市
Pc = cumsum(P);
target_index = find(Pc >= rand);
target = allow(target_index(1));
Table(i,j) = target;
end
end
% 计算各个蚂蚁的路径距离
Length = zeros(m,1);
for i = 1:m
Route = Table(i,:);
for j = 1:(n - 1)
Length(i) = Length(i) + D(Route(j),Route(j + 1));
end
Length(i) = Length(i) + D(Route(n),Route(1));
end
% 计算最短路径距离及平均距离
if iter == 1
[min_Length,min_index] = min(Length);
Length_best(iter) = min_Length;
Length_ave(iter) = mean(Length);
Route_best(iter,:) = Table(min_index,:);
else
[min_Length,min_index] = min(Length);
Length_best(iter) = min(Length_best(iter - 1),min_Length);
Length_ave(iter) = mean(Length);
if Length_best(iter) == min_Length
Route_best(iter,:) = Table(min_index,:);
else
Route_best(iter,:) = Route_best((iter-1),:);
end
end
% 更新信息素
Delta_Tau = zeros(n,n);
% 逐个蚂蚁计算
for i = 1:m
% 逐个城市计算
for j = 1:(n - 1)
Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i);
end
Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i);
end
Tau = (1-rho) * Tau + Delta_Tau;
% 迭代次数加1,清空路径记录表
iter = iter + 1;
Table = zeros(m,n);
end
% 结果显示
[Shortest_Length,index] = min(Length_best);
Shortest_Route = Route_best(index,:);
disp(['最短距离:' num2str(Shortest_Length)]);
disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);
% 绘图
figure(1)
plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
grid on
for i = 1:size(citys,1)
text(citys(i,1),citys(i,2),[' ' num2str(i)]);
end
text(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),' 起点');
text(citys(Shortest_Route(end),1),citys(Shortest_Route(end),2),' 终点');
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
title(['蚁群算法优化路径(最短距离:' num2str(Shortest_Length) ')'])
figure(2)
plot(1:iter_max,Length_best,'b',1:iter_max,Length_ave,'r:')
legend('最短距离','平均距离')
xlabel('迭代次数')
ylabel('距离')
title('各代最短距离与平均距离对比')
结果:

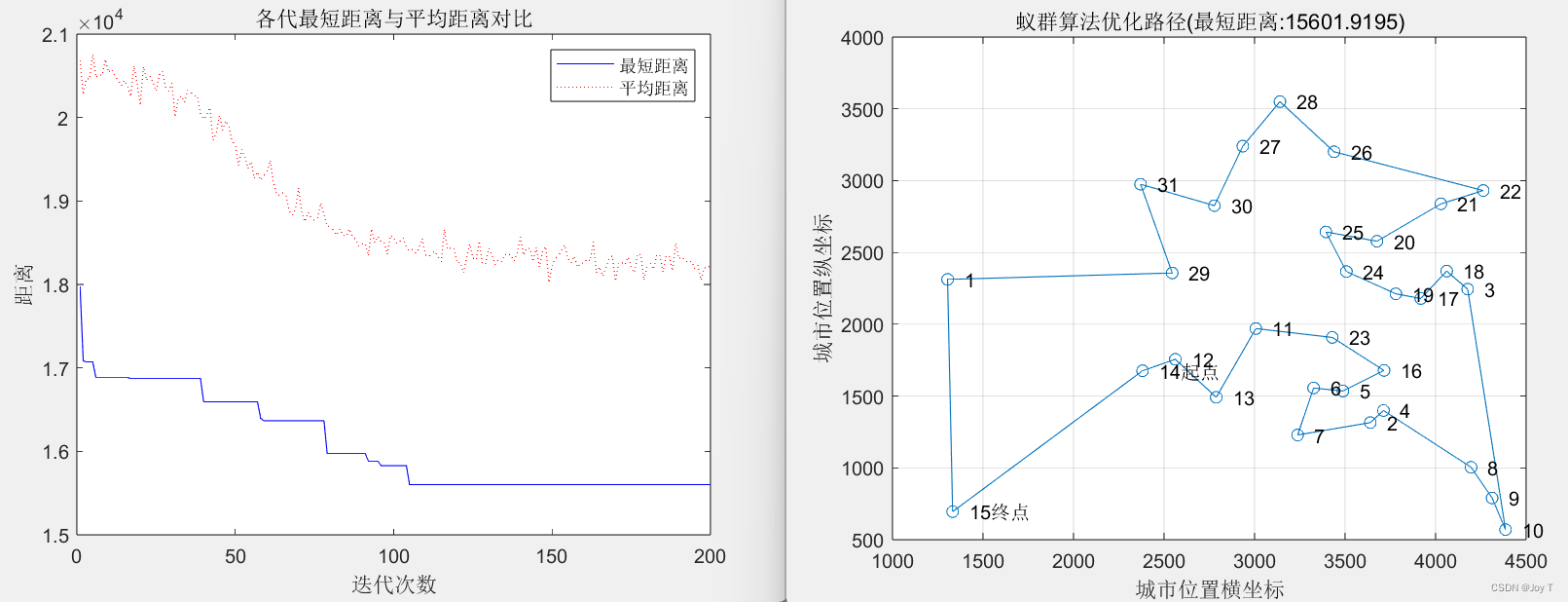
一般来说,使用两种方法对比一下,然后选结果好的作为最终结果就挺不错的了,因为优化类问题没有这么简单,能做出来就很棒了。
联合使用蚁群算法和模拟退火
1. 使用蚁群算法找到一个初始解
2. 将该解作为模拟退火算法的初始解
3. 使用模拟退火算法进行优化
4. 输出最终结果
简单来说,就是使用蚁群算法先求出一个最短路径作为初始解,然后把它作为模拟退火的最优解,使用退火进行进一步的优化。

但是作者发现效果并不好,其迭代曲线啊,还是和之前一样从高高的位置迭代,结果也不好,肯定是模拟退火的原因,于是作者有了以下想法:当已经有了一个不错的初始解(通过蚁群算法获得)时,模拟退火算法的参数需要进行相应的调整以避免在初始阶段进行过大的“跳跃”。
可以减小初始温度、减小冷却速度(都能使得搜索更充分)、修改接受准则以更倾向于接受与当前解相近的解和设置交换城市函数的交换“步长”。
修改接受准则,加入一些额外条件或参数以减小接受差解的概率。例如,可以使用一个基于当前温度和解的差异的函数来调整接受概率。
if (diff < 0) || (rand < exp(-diff / (temperature * some_factor)))
route = new_route;
current_dist = new_dist;
end
其中 some_factor 是一个你可以调整的参数,用来控制接受新解的概率。
在交换城市时,可以只考虑交换相邻城市的位置,这会限制每次迭代的“步长”。
function new_route = swapCities2(route)
n = length(route);
idx = randi(n-1);
new_route = route;
new_route([idx idx+1]) = route([idx+1 idx]);
end
经过作者尝试,这种设置还是蛮动态的,不一定都需要改,改多了就很难得到更小的解,作者就没用新的交换函数(可能是因为数据太少)。得到结果如下:
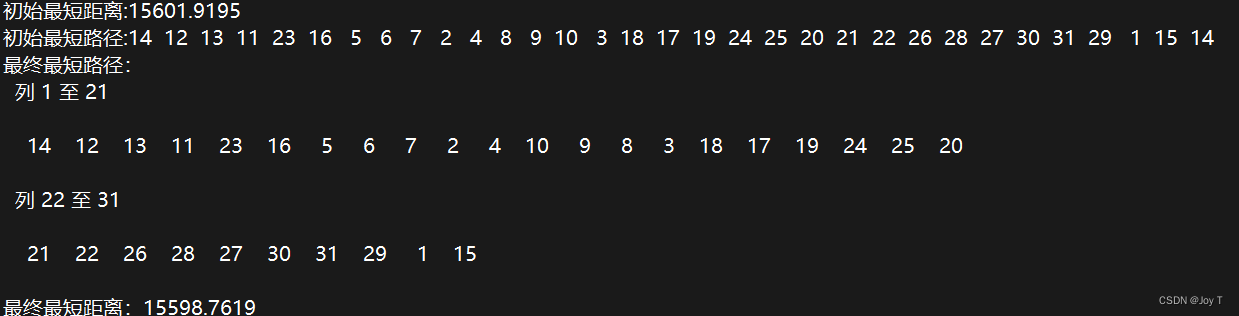
最终结合代码如下:
%% 二者结合
% 蚁群算法求解TSP问题
% 计算城市间相互距离
n = size(citys,1);
D = zeros(n,n);
for i = 1:n
for j = 1:n
if i ~= j
D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));
else
D(i,j) = 1e-4;
end
end
end
% 初始化参数
m = 80; % 蚂蚁数量
alpha = 1; % 信息素重要程度因子
beta = 5; % 启发函数重要程度因子
rho = 0.1; % 信息素挥发因子
Q = 1; % 常系数
Eta = 1./D; % 启发函数
Tau = ones(n,n); % 信息素矩阵
Table = zeros(m,n); % 路径记录表
iter = 1; % 迭代次数初值
iter_max = 200; % 最大迭代次数
Route_best = zeros(iter_max,n); % 各代最佳路径
Length_best = zeros(iter_max,1); % 各代最佳路径的长度
Length_ave = zeros(iter_max,1); % 各代路径的平均长度
% 迭代寻找最佳路径
while iter <= iter_max
% 随机产生各个蚂蚁的起点城市
start = zeros(m,1);
for i = 1:m
temp = randperm(n);
start(i) = temp(1);
end
Table(:,1) = start;
% 构建解空间
citys_index = 1:n;
% 逐个蚂蚁路径选择
for i = 1:m
% 逐个城市路径选择
for j = 2:n
tabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表)
allow_index = ~ismember(citys_index,tabu);
allow = citys_index(allow_index); % 待访问的城市集合
P = allow;
% 计算城市间转移概率
for k = 1:length(allow)
P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta;
end
P = P/sum(P);
% 轮盘赌法选择下一个访问城市
Pc = cumsum(P);
target_index = find(Pc >= rand);
target = allow(target_index(1));
Table(i,j) = target;
end
end
% 计算各个蚂蚁的路径距离
Length = zeros(m,1);
for i = 1:m
Route = Table(i,:);
for j = 1:(n - 1)
Length(i) = Length(i) + D(Route(j),Route(j + 1));
end
Length(i) = Length(i) + D(Route(n),Route(1));
end
% 计算最短路径距离及平均距离
if iter == 1
[min_Length,min_index] = min(Length);
Length_best(iter) = min_Length;
Length_ave(iter) = mean(Length);
Route_best(iter,:) = Table(min_index,:);
else
[min_Length,min_index] = min(Length);
Length_best(iter) = min(Length_best(iter - 1),min_Length);
Length_ave(iter) = mean(Length);
if Length_best(iter) == min_Length
Route_best(iter,:) = Table(min_index,:);
else
Route_best(iter,:) = Route_best((iter-1),:);
end
end
% 更新信息素
Delta_Tau = zeros(n,n);
% 逐个蚂蚁计算
for i = 1:m
% 逐个城市计算
for j = 1:(n - 1)
Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i);
end
Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i);
end
Tau = (1-rho) * Tau + Delta_Tau;
% 迭代次数加1,清空路径记录表
iter = iter + 1;
Table = zeros(m,n);
end
% 结果显示
[Shortest_Length,index] = min(Length_best);
Shortest_Route = Route_best(index,:);
disp(['初始最短距离:' num2str(Shortest_Length)]);
disp(['初始最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);
% 初始化参数
temperature = 200;
final_temperature = 1;
cooling_rate = 0.9;
time_temperature = 1;
time_tuihuo = 100;
% 初始路径就是蚁群算法得到的路径
route = Shortest_Route;
current_dist = Shortest_Length;
% 存储每次迭代的距离
distances = [];
%控制接受新解的概率
some_factor=0.3;
while temperature > final_temperature
for i = 1:time_tuihuo
% 交换两个城市的位置来产生新的路径
new_route = swapCities(route);
new_dist = total_distance(new_route, citys);
diff = new_dist - current_dist;
% 使用 Metropolis 准则来决定是否接受新路径
if (diff < 0) || (rand < exp(-diff / (temperature*some_factor)))
route = new_route;
current_dist = new_dist;
time_temperature = time_temperature + 1;
end
end
% 存储当前的总距离
distances = [distances, current_dist];
% 降温
temperature = temperature * cooling_rate;
end
% 输出最终结果
disp('最终最短路径:');
disp(route);
fprintf('最终最短距离:%.4f\n', current_dist);
% 绘制最终路径
figure;
plot(citys(:,1), citys(:,2), 'o'); % 绘制城市
hold on;
% 绘制路径
for i = 1:(length(route)-1)
plot([citys(route(i), 1), citys(route(i+1), 1)], ...
[citys(route(i), 2), citys(route(i+1), 2)], 'k-');
end
% 绘制从最后一个城市到第一个城市的路径
plot([citys(route(end), 1), citys(route(1), 1)], ...
[citys(route(end), 2), citys(route(1), 2)], 'k-');
hold off;
title('最终路径');
% 绘制迭代曲线图
figure;
plot(distances);
title('迭代过程中的总距离变化');
xlabel('迭代次数');
ylabel('总距离');可能的方法还有:使用模拟退火算法来优化蚁群算法的一些参数,或者在每一次迭代后使用模拟退火算法来进行局部搜索。都是作者推荐的方法哦!