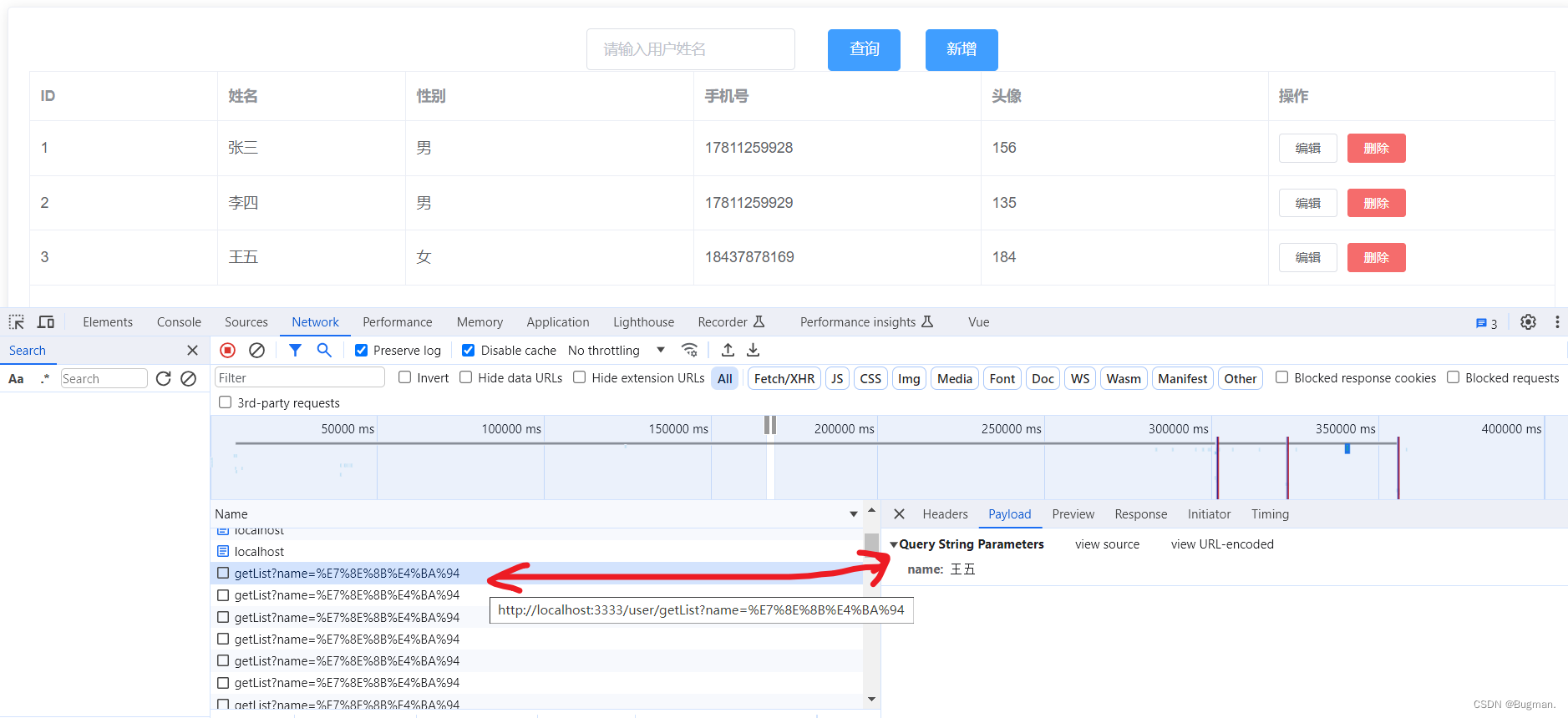
我们在中学阶段就遇到过线性规划问题,主要是二维的情况,而求解的方法一般是非常直观、高效的图解法。根据过往的经验,线性规划问题的最优目标值一般在可行域的顶点处取得,那么本文就对这个问题进行更深入的探讨,维度也从二维推广至高维,内容主要包括以下问题:
- 线性规划问题的可行域有哪些性质?
- 线性规划问题的可行域顶点有哪些特点?
- 为什么可行域的顶点有最优解?
- 顶点的数学描述?
- 高维模型有哪些性质?
1. 线性规划模型的一些基本概念
为了便于描述,我们首先给出几个基本的概念:
- 可行域(可行集):满足线性规划问题所有约束条件的决策变量集合称为可行集(图解法的过程中称为可行域)。
- 可行解:在可行域内的解(决策变量)称为可行解。
- 基本解:能够使线性规划问题的某些约束条件等式成立的解称为基本解。此时,等式成立的约束条件称为起作用的约束,其构成线性方程组得到唯一解,即基本解。注意:基本解不一定在可行域内,因为并不一定满足所有的约束条件。
补充:非齐次线性方程组 AX=b 有唯一解的条件是,系数矩阵与增广矩阵的秩相同且都等于 X 的维度n,即r( A A A) = r( A ^ \hat{A} A^) = n,其中增广矩阵 A ^ = [ A , b ] \hat{A} =[A, b] A^=[A,b]。详细说明过程可以参考博客:【线性代数】齐次与非齐次线性方程组有解的条件
- 基本可行解:在可行域的基本解称为基本可行解。
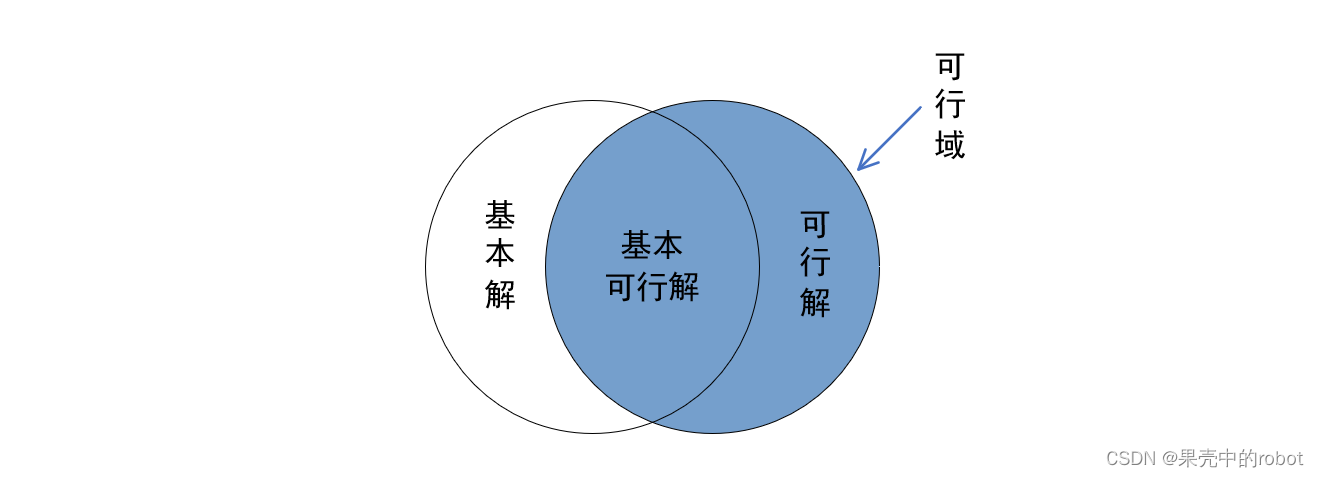
直观而言,基本可行解就是可行域的顶点,且顶点个数总是有限的。
2. 线性规划问题的可行集与凸集
凸集和凸集顶点的定义
如果某个集合中任意两点连起来的直线都属于该集合,则称其为凸集,否则为非凸集,如下图所示:

凸集数学定义: Ω 是凸集,当且仅当对 ∀ 0 < α < 1 和任意的 X 1 , X 2 ∈ Ω 均有下式成立: α X 1 + ( 1 − α ) X 2 ∈ Ω \Omega是凸集,当且仅当对~ \forall~0 < \alpha < 1 和 任意的 X_1, X_2 \in \Omega均有下式成立:\alpha X_1 + (1-\alpha)X_2 \in \Omega Ω是凸集,当且仅当对 ∀ 0<α<1和任意的X1,X2∈Ω均有下式成立:αX1+(1−α)X2∈Ω
如果凸集内的一点不在凸集内任何不同的两点连起来的直线上,则称该点为该凸集的顶点,如下所示:
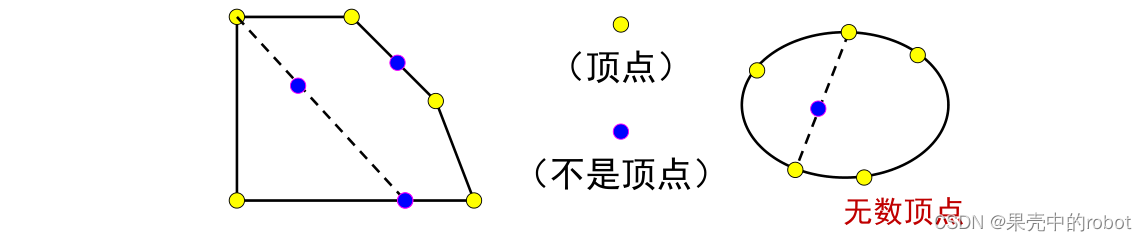
凸集顶点的数学定义: X ∈ Ω 是凸集的顶点,当且仅当对不存在实数 0 < α < 1 和 X 1 , X 2 ∈ Ω , X 1 ≠ X 2 满足: X = α X 1 + ( 1 − α ) X 2 X\in\Omega是凸集的顶点,当且仅当对不存在实数~0 < \alpha < 1 和 X_1, X_2 \in \Omega,X_1\neq X_2满足:X = \alpha X_1 + (1-\alpha)X_2 X∈Ω是凸集的顶点,当且仅当对不存在实数 0<α<1和X1,X2∈Ω,X1=X2满足:X=αX1+(1−α)X2
线性规划问题的多面体模型

根据该模型以及凸集的定义可以得到:
- 线性规划多面体模型的可行集是凸集。
- 线性规划多面体模型的基本可行解是凸集的顶点。
证明过程暂略。
3. 线性规划可行域的顶点中有最优解
我们分三种情况进行讨论,以说明可行域的顶点处一定有最优解。
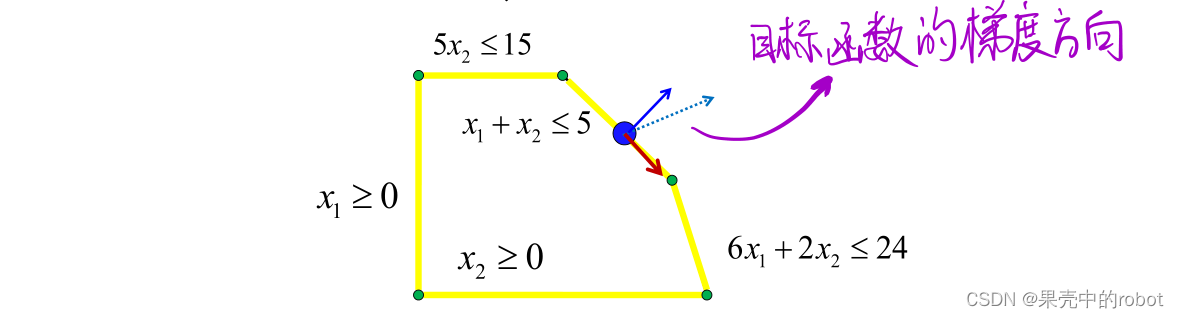
第一种情况:如果可行解没有起作用约束(约束条件中不等式变为等式,则称该约束为起作用约束),即可行解是可行域的内点,那么沿着梯度方向必定可以改进目标函数,所以此时不可能是最优解,如下图所示。

第二种情况:如果可行解不是起作用约束的唯一解,则必定有非零向量和起作用约束的所有法线垂直(如下图蓝色点和蓝实线向量),那么此时将梯度方向投影到蓝色向量的垂直空间得到一个向量(红色向量),则沿此方向前进可以改进目标函数,因此该可行解不可能是最优解。
第三种情况:如果可行解不是起作用约束的唯一解,但梯度如下所示,和所有起作用约束的法线垂直,此时蓝点是最优解,但是沿着红色方向前进可以得到至少增加一个起作用约束的最优解,因此也可得到是最优解的顶点(此时目标函数有无穷多最优解)。
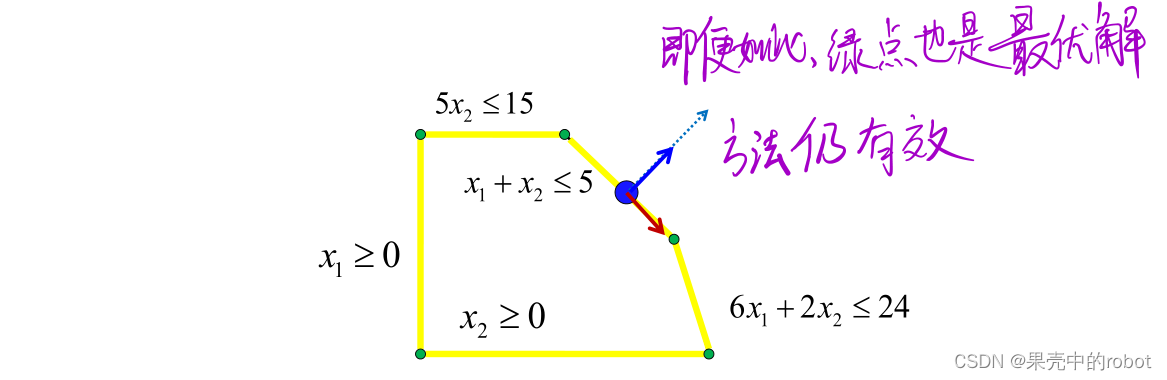
综上,基本可行解是线性规划问题的可行域顶点,该问题的最优解一定存在于基本可行解中。
4. 标准模型顶点的数学描述
回顾:线性规划的标准模型
线性规划标准模型的介绍,可以参考博客:【最优化理论】线性规划的标准模型与基本假定,这里简要回顾一下。
在最优化理论中考虑的线性规划标准模型为:
max C T X s.t. A X = b ⃗ X ≥ 0 \max ~~C^TX ~~~ \\ \text{s.t.} ~~AX = \vec{b} \\ ~~~~~~~~~~X ≥ 0 max CTX s.t. AX=b X≥0
其中, C ∈ R n , X ∈ R n , A ∈ R m × n C \in R^n,X \in R^n,A \in R^{m\times n} C∈Rn,X∈Rn,A∈Rm×n,并假定:
- 系数矩阵 A A A 的列数大于其行数,即 n > m;
- A A A 的行向量线性无关,即A行满秩。
max C T X \max C^TX maxCTX 是该线性规划问题的目标函数, A X = b ⃗ AX = \vec{b} AX=b 是约束条件中的等式约束, X ≥ 0 X ≥ 0 X≥0 是对决策变量的非负性约束。
顶点的充要条件
线性规划标准模型的等式约束描述如下:
∑
j
=
1
n
a
i
j
x
j
=
b
i
,
∀
1
≤
i
≤
m
⇒
∑
j
=
1
n
[
a
1
j
a
2
j
⋮
a
m
j
]
x
j
=
[
b
1
b
2
⋮
b
m
]
⇒
∑
j
=
1
n
P
j
x
j
=
b
⃗
,
P
j
=
(
a
1
j
,
⋯
,
a
m
j
)
T
,
∀
1
≤
j
≤
n
\sum_{j=1}^{n} a_{ij}x_j = b_i,~\forall~1\leq i \leq m \qquad \Rightarrow \qquad \sum_{j=1}^{n} \begin{bmatrix} a_{1j} \\ a_{2j} \\ \vdots \\ a_{mj} \end{bmatrix}x_j = \begin{bmatrix} b_{1} \\ b_{2} \\ \vdots \\ b_{m} \end{bmatrix} \\ \Rightarrow \sum_{j=1}^{n} P_{j}x_j = \vec{b}, \quad P_j = (a_{1j}, \cdots, a_{mj})^T, \quad \forall~1\leq j \leq n
j=1∑naijxj=bi, ∀ 1≤i≤m⇒j=1∑n
a1ja2j⋮amj
xj=
b1b2⋮bm
⇒j=1∑nPjxj=b,Pj=(a1j,⋯,amj)T,∀ 1≤j≤n
根据标准模型的非负性约束条件可知,对于决策变量 X = ( x 1 , x 2 , . . . , x m ) T X = (x_1, x_2, ..., x_m)^T X=(x1,x2,...,xm)T,其分量 x j x_j xj 要么大于0,要么等于0,因此可以对任意的 X ∈ Ω X\in\Omega X∈Ω 进行如下划分(需注意:n > m):
x j > 0 , j = k ( 1 ) , k ( 2 ) , . . . , k ( m ^ ) ; x j = 0 , j = k ( m + 1 ^ ) , . . . , k ( n ) x_j > 0, j = k(1), k(2), ..., k(\hat{m}); \\ x_j = 0, j = k(\hat{m+1}), ..., k(n) xj>0,j=k(1),k(2),...,k(m^);xj=0,j=k(m+1^),...,k(n)
进而可以得到结论: 当且仅当 ∑ t = 1 m ^ P j ( t ) x j ( t ) = b ⃗ 的解唯一时, X 是顶点 . 当且仅当 \sum_{t=1}^{\hat{m}}P_{j(t)}x_{j(t)} = \vec{b}的解唯一时,X是顶点. 当且仅当t=1∑m^Pj(t)xj(t)=b的解唯一时,X是顶点.
解释:因为基本可行解是所有起作用约束的唯一解,而起作用约束就是不等式变为等式的那些约束。
标准模型顶点的等价描述之一
如果把 X ∈ Ω = { X ∈ R n ∣ ∑ j = 1 n P j x j = b ⃗ , X ≥ 0 } X\in \Omega = \{X\in\R^n | \sum_{j=1}^{n}P_{j}x_j = \vec{b},~X\ge0 \} X∈Ω={X∈Rn∣∑j=1nPjxj=b, X≥0} 的非零分量成为正分量,那么任何可行解是顶点的充分必要条件是:
其正分量对应的系数向量 P j 线性无关 ⇔ 如果 X ∈ Ω 划分为 x j > 0 , j = k ( 1 ) , k ( 2 ) , . . . , k ( m ^ ) ; x j = 0 , j = k ( m + 1 ^ ) , . . . , k ( n ) 其为顶点的充要条件是 P j 线性无关 ( j = k ( 1 ) , . . . , k ( m ^ ) ) . 其正分量对应的系数向量P_j线性无关~\Leftrightarrow~如果 X\in\Omega划分为 \\ x_j > 0, j = k(1), k(2), ..., k(\hat{m}); \\ x_j = 0, j = k(\hat{m+1}), ..., k(n) \\其为顶点的充要条件是 P_j 线性无关(j=k(1), ..., k(\hat{m})). 其正分量对应的系数向量Pj线性无关 ⇔ 如果X∈Ω划分为xj>0,j=k(1),k(2),...,k(m^);xj=0,j=k(m+1^),...,k(n)其为顶点的充要条件是Pj线性无关(j=k(1),...,k(m^)).
标准模型顶点的等价描述之二
如果 ( P 1 , . . . , P n ) (P_1, ..., P_n) (P1,...,Pn) 是行满秩矩阵,那么 X X X是可行集 Ω = { X ∈ R n ∣ ∑ j = 1 n P j x j = b ⃗ , X ≥ 0 } \Omega = \{X\in\R^n | \sum_{j=1}^{n}P_{j}x_j = \vec{b},~X\ge0 \} Ω={X∈Rn∣∑j=1nPjxj=b, X≥0} 的顶点充要条件是 :
存在可逆方阵 ( P k ( 1 ) , . . . , P k ( m ) ) ,可以把 X 的分量划分为 x k ( j ) , j = 1 , . . . , n ,使满足: [ x k ( 1 ) ⋮ x k ( m ) ] = ( P k ( 1 ) , . . . , P k ( m ) ) − 1 b ⃗ ; x k ( j ) = 0 , ∀ m + 1 ≤ j ≤ n 存在可逆方阵 \left(P_{k(1)}, ..., P_{k(m)}\right),可以把X的分量划分为x_{k(j)}, j = 1, ..., n,使满足:\\ \begin{bmatrix} x_{k(1)} \\ \vdots \\ x_{k(m)} \end{bmatrix} = \left(P_{k(1)}, ..., P_{k(m)}\right)^{-1} \vec{b}~;\quad x_{k(j)}=0,~\forall m+1 \leq j \leq n 存在可逆方阵(Pk(1),...,Pk(m)),可以把X的分量划分为xk(j),j=1,...,n,使满足: xk(1)⋮xk(m) =(Pk(1),...,Pk(m))−1b ;xk(j)=0, ∀m+1≤j≤n
说明:
对于
A
X
=
b
⃗
,
X
≥
0
,其中
A
∈
R
m
×
n
,
m
<
n
,
A
行满秩,则
A
X
=
b
⃗
可以分解为
:
A
X
=
b
⃗
⇒
[
B
N
]
[
X
B
X
N
]
=
b
⃗
,
其中
B
∈
R
m
×
m
可逆,
N
∈
R
m
×
(
n
−
m
)
,满足
B
⋅
X
B
+
N
⋅
X
N
=
b
⃗
⇒
X
B
=
B
−
1
⋅
b
⃗
≥
0
,
X
N
=
0
,则
X
=
[
X
B
T
,
X
N
T
]
T
均是可行域的顶点
.
对于AX=\vec{b},~X\ge0,其中A\in R^{m\times n}, m<n,A行满秩,则~AX=\vec{b}~可以分解为:\\ AX=\vec{b} \quad \Rightarrow \quad [B\quad N] \begin{bmatrix} X_B \\ X_N \end{bmatrix} = \vec{b}~,~其中 B\in R^{m\times m}可逆,N\in R^{m\times (n-m)},满足\\ B\cdot X_B + N\cdot X_N = \vec{b} \\ \Rightarrow \quad X_B = B^{-1}\cdot \vec{b} \ge 0, X_N = 0,则X= [X_B^T, X_N^T]^T均是可行域的顶点.
对于AX=b, X≥0,其中A∈Rm×n,m<n,A行满秩,则 AX=b 可以分解为:AX=b⇒[BN][XBXN]=b , 其中B∈Rm×m可逆,N∈Rm×(n−m),满足B⋅XB+N⋅XN=b⇒XB=B−1⋅b≥0,XN=0,则X=[XBT,XNT]T均是可行域的顶点.
5. 线性规划标准模型的重要概念和性质
基阵、基本解和基本可行解
称可逆矩阵 ( P k ( 1 ) , . . . , P k ( m ) ) \left(P_{k(1)}, ..., P_{k(m)}\right) (Pk(1),...,Pk(m))为基阵B,称其分量由下式决定的 X X X 为基本解,
[ x k ( 1 ) ⋮ x k ( m ) ] = ( P k ( 1 ) , . . . , P k ( m ) ) − 1 b ⃗ ; x k ( j ) = 0 , ∀ m + 1 ≤ j ≤ n \begin{bmatrix} x_{k(1)} \\ \vdots \\ x_{k(m)} \end{bmatrix} = \left(P_{k(1)}, ..., P_{k(m)}\right)^{-1} \vec{b}~;\quad x_{k(j)}=0,~\forall m+1 \leq j \leq n xk(1)⋮xk(m) =(Pk(1),...,Pk(m))−1b ;xk(j)=0, ∀m+1≤j≤n
需要注意的是,基本解有可能是相交在可行域外的顶点。我们称可行的基本解(在可行域内)为基本可行解;称基阵对应变量为基变量 X B X_B XB,其余变量为非基变量 X N X_N XN。
线性规划标准模型的基本定理
-
一个标准模型的线性规划问题若有可行解,则至少存在一个基本可行解(顶点)。
证明思路:系数矩阵A行满秩,构造可逆矩阵B即可。
注意:标准模型一定有顶点是因为有非负性条件约束。换句话说,如果一般(非标准模型)的线性规划问题有可行解,则并不一定有基本可行解(顶点),比如二维的例子: x 1 + x 2 = 3 x_1 + x_2=3 x1+x2=3,没有非负性约束,则可行域从负无穷延伸到正无穷,就没有顶点。 -
一个标准模型的线性规划问题若有有限的最优目标值,则一定存在一个基本可行解是最优解。
这个定理的等价描述是:若一个线性规划问题在两个顶点上达到最优值,则该线性规划问题必有无穷多个最优解。
证明思路:可以用反证法。
至此,线性规划问题的理论分析已经结束,也就是说已经从数学上解决了线性规划问题,即只需要从顶点中搜索最优解即可。
但是,真正要将线性规划理论应用到实际中,还面临诸多工程问题,比如计算效率问题(求逆的运算量非常大)、如何使用计算机高效解决线性规划问题等等,因此后面会介绍在工程实践上最常用的算法——单纯形算法。需要注意的是,单纯形算法虽然应用广泛,但并没有任何数学上的贡献,而都是工程应用实践的贡献。当然,对于解决现实世界中问题而言,理论和实践都很重要。








![2023年中国体育赛事行业现状及趋势分析:体育与科技逐步融合,推动产业高质量发展[图]](https://img-blog.csdnimg.cn/img_convert/2fc2b3f17b2b5ff4d1b90540be97d9f9.png)
