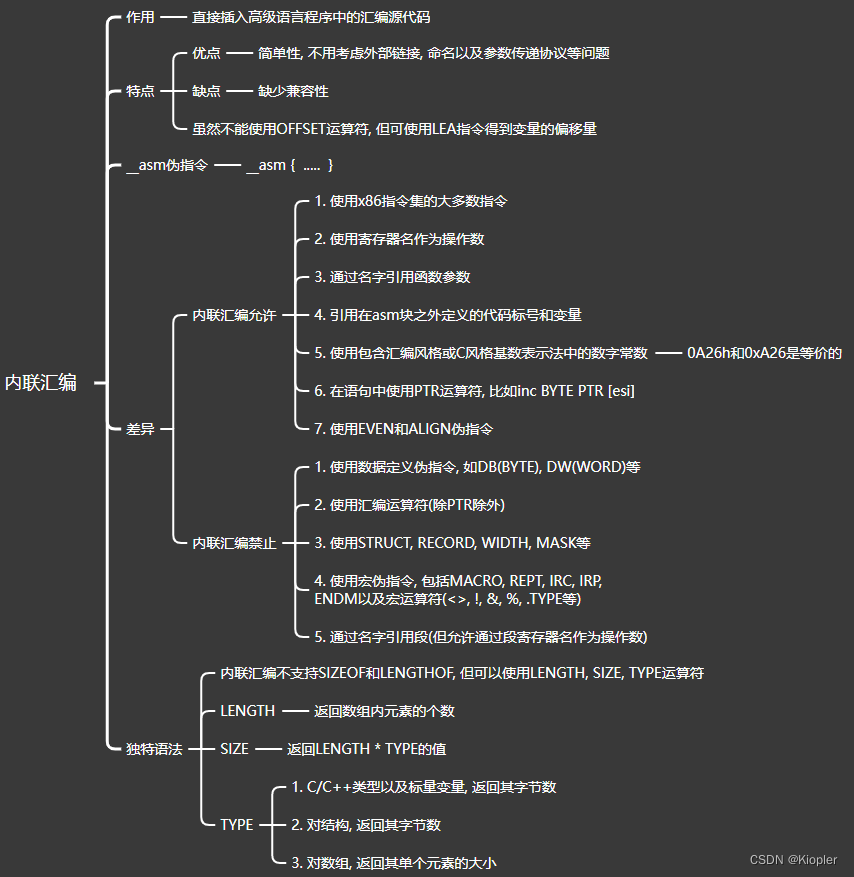
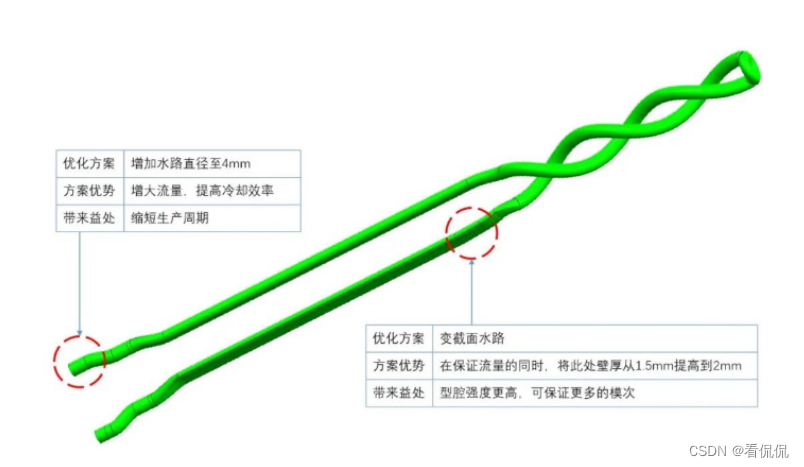
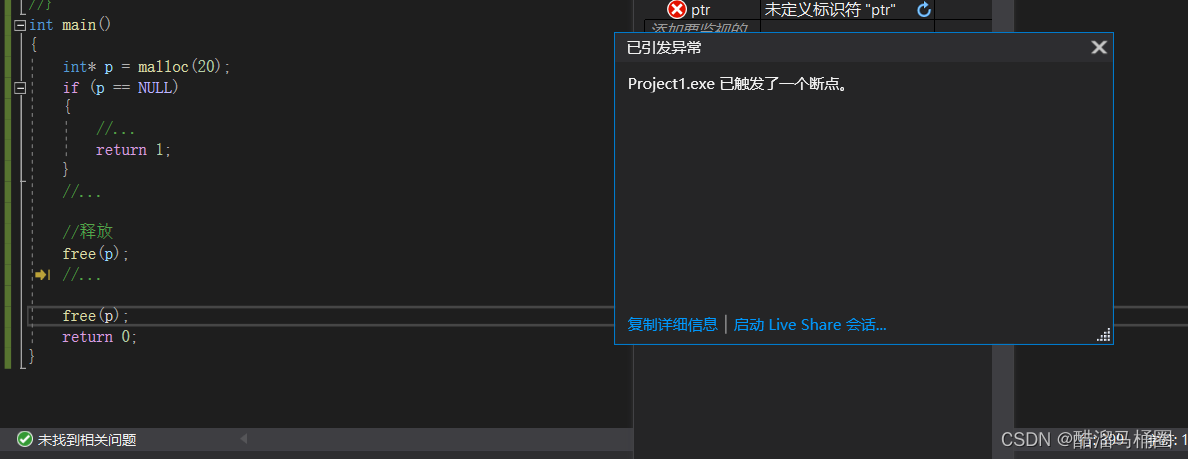
https://codeforces.com/problemset/problem/446/E

把官方题解翻译了一遍

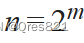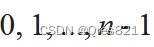考虑暴力，肯定想到dp，然后变成矩阵。设用代替
（这样子数之间的差值不会变化，但对于问题的处理能方便很多）

我们先令（也就是初始时的方案数），然后尝试构造转移矩阵 $B$

$B$ 的大小应该为 $n\times n$，每个格子对应两点之间的路径条数，也就是

我们要算 $t$ 填后的 $B$，也就是 $B^t$

所以答案为

考虑如何不暴力地构造 $B$。由于 $B$ 非常大，所以我们考虑分治构造+构造过程中乘到 $A$ 上面。

先打表 $m=3$ 时的 $B_3$：

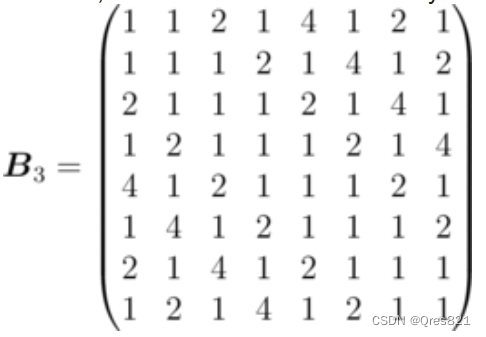
然后可以观察到一些规律：

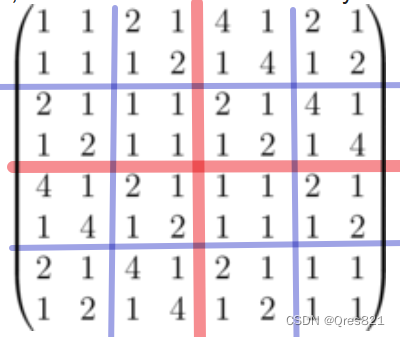
我们可以发现 $B$ 之间的类似递推的构造方式：

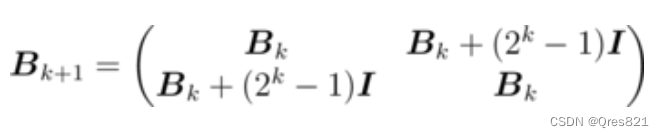
其中

发现其实可以递归下去，所以本质上，其必然可以表示成只存在 $B_0$ 和 $I$ 的形式：

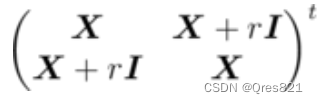
我们刚刚提到要求 $B$ 的过程中在线维护 $A$

但是观察上面的式子。$A$ 乘上一个矩阵的多次幂难以拆开，所以我们可以考虑把 $t$ 放到矩阵每一项上

但是我们直接乘到每一项上对于结果的求解似乎在时间上也无法进行优化。所以我们应该构造一个矩阵，满足其适用于递归进入子问题。

考虑这样子构造：

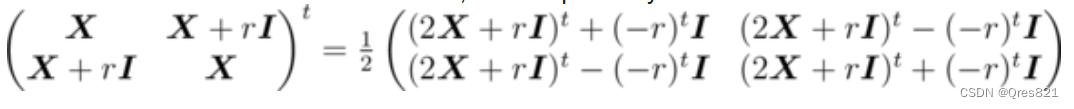
这样子构造，我们要求的是 和

后面的明显可以在线求，前面的考虑递归

我们要对 $A$ 进行分治。那么只有前半部分和后半部分有用，内部具体是什么在当层分治节点并不重要，所以我们设目前 $A=$

然后我们乘一下上面的矩阵试试：

看起来很有用。拿现在考虑递归求解 时，我们还要考虑外面对这里的影响，所以我们必须考虑推广到：

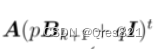
注意，我们现在其实是用 表示 $B_m^t$

所以考虑把上式换成用过 $B_k$ 表示的形式，我们按照之前的式子展开：

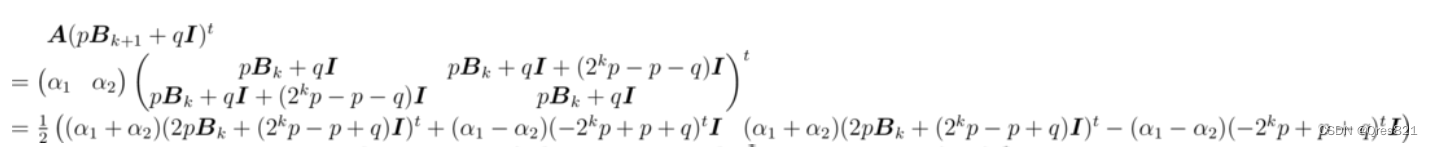
可以发现，我们现在已经消除到$B_{k+1}$，变成了纯用 $B_k$ 表示的式子了

把同类型划出来：

黄色部分可以直接求解，对于我们则进行递归求解

#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar(); while(ch<'0'||
ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
//mt19937 rand(time(0));
//mt19937_64 rand(time(0));
//srand(time(0));
#define N 40000010
//#define M
#define mo 1051131
int pw(int a, int b) {
	int ans=1; 
	while(b) {
		if(b&1) ans*=a; 
		a*=a; b>>=1; 
		ans%=mo; a%=mo; 
	}
	return ans; 
}
const int iv2=525566; 
int n, m, i, j, k, T;
int ans, s, t, a[N]; 

void solve(int k, int p, int q) { //计算k，则应由k-1转移过来 
//	printf("[%lld] %lld %lld\n", k, p, q); 
	if(!k) return a[0]=a[0]*pw(p+q, t)%mo, void(); 
	//B0=1=I, so A=(A*B0')^t=(A*B0^(p+q))^t
	int tw=(1ll<<k-1), i, x, y, G=pw(-(1ll<<k-1)*p+p+q, t)%mo; 
//	printf(">> %lld %lld\n", tw, G); 
	for(i=0; i<(1<<k-1); ++i) {
		x=a[i]; y=a[i+tw]; 
		a[i]=(x+y)%mo; //低位拿下去分治 
		a[i+tw]=(x-y)*G%mo; //(a1-a2)*(-2^k*p+p+q)
	}
	solve(k-1, 2*p%mo, ((1ll<<k-1)*p-p+q)%mo); 
	for(i=0; i<(1<<k-1); ++i) {
		x=a[i]; y=a[i+tw]; 
		a[i]=(x+y)*iv2%mo; //代公式 
		a[i+tw]=(x-y)*iv2%mo; 
	}
}

signed main()
{
//	freopen("in.txt", "r", stdin);
//	freopen("out.txt", "w", stdout);
//	T=read();
//	while(T--) {
//
//	}
//	printf(">> %lld %lld\n", iv2, iv2*2%mo); 
	m=read(); t=read(); s=read(); 
	n=(1ll<<m); 
	for(i=1; i<=s; ++i) a[i]=read(); 
	for(; i<=n; ++i) a[i]=(101*a[i-s]+10007)%mo; 
	a[0]=a[n]; 
//	for(i=0; i<n; ++i) printf("%lld ", a[i]); printf("\n"); 
	solve(m, 1, 0); // 初始ans=A*Bm （=1*Bm+0*I） 
	for(i=0; i<n; ++i) ans^=((a[i]%mo+mo)%mo); 
	printf("%lld", ans); 
	return 0;
}