路径 - 蓝桥云课 (lanqiao.cn)

题目分析 

求最短路问题，有多种解法，下面介绍两种蓝桥杯最常用到的两种解法

方法一

Floyd（求任意两点之间的最短路）注：不能有负权回路

初始化每个点到每个点的距离都为0x3f这样才能对比求出最短路

由题意先将ab差的绝对值小于等于21的边的边权赋予，还有自己到自己的边为0

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 3000;
int ans = 0x3f;
int d[N][N];
int gcd(int a, int b)
{
	return b == 0 ? a : gcd(b, a % b);
}
int lcm(int a, int b)
{
	return a * b / gcd(a, b);
}
int main()
{	
	memset(d, 0x3f, sizeof d);
	for(int i = 1; i <= 2021; i ++)
	{
		for(int j = 1; j <= 2021; j ++)
		{
			if(abs(i - j) <= 21)
			{
				d[i][j] = min(d[i][j], lcm(i, j));
			}
		}
	}
	for(int i = 1; i <= 2021; i ++)d[i][i] = 0;
	for(int k = 1; k <= 2021; k ++)
	{
		for(int i = 1; i <= 2021; i ++)
		{
			for(int j = 1; j <= 2021; j ++)
			{
				d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
			}
		}
	}
	cout << d[1][2021];
	return 0;
}

答案：10266837

方法二

Dijkstra（任意一点到所有点的最短路）

第一步：初始化距离 dist[1] = 0, dist[i] = +∞

第二步：找到当前没有确定点的最小值，找到最小的点之后用这个点去更新它到所有点的距离

 

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const int N = 2e5 + 10;
int e[N], ne[N], w[N], h[N], idx, d[N];
bool st[N]; 
int gcd(int a, int b)
{
	return b == 0 ? a : gcd(b, a % b);
}
int lcm(int a, int b)
{
	return a * b / gcd(a, b);
}
void add(int a, int b, int c)
{
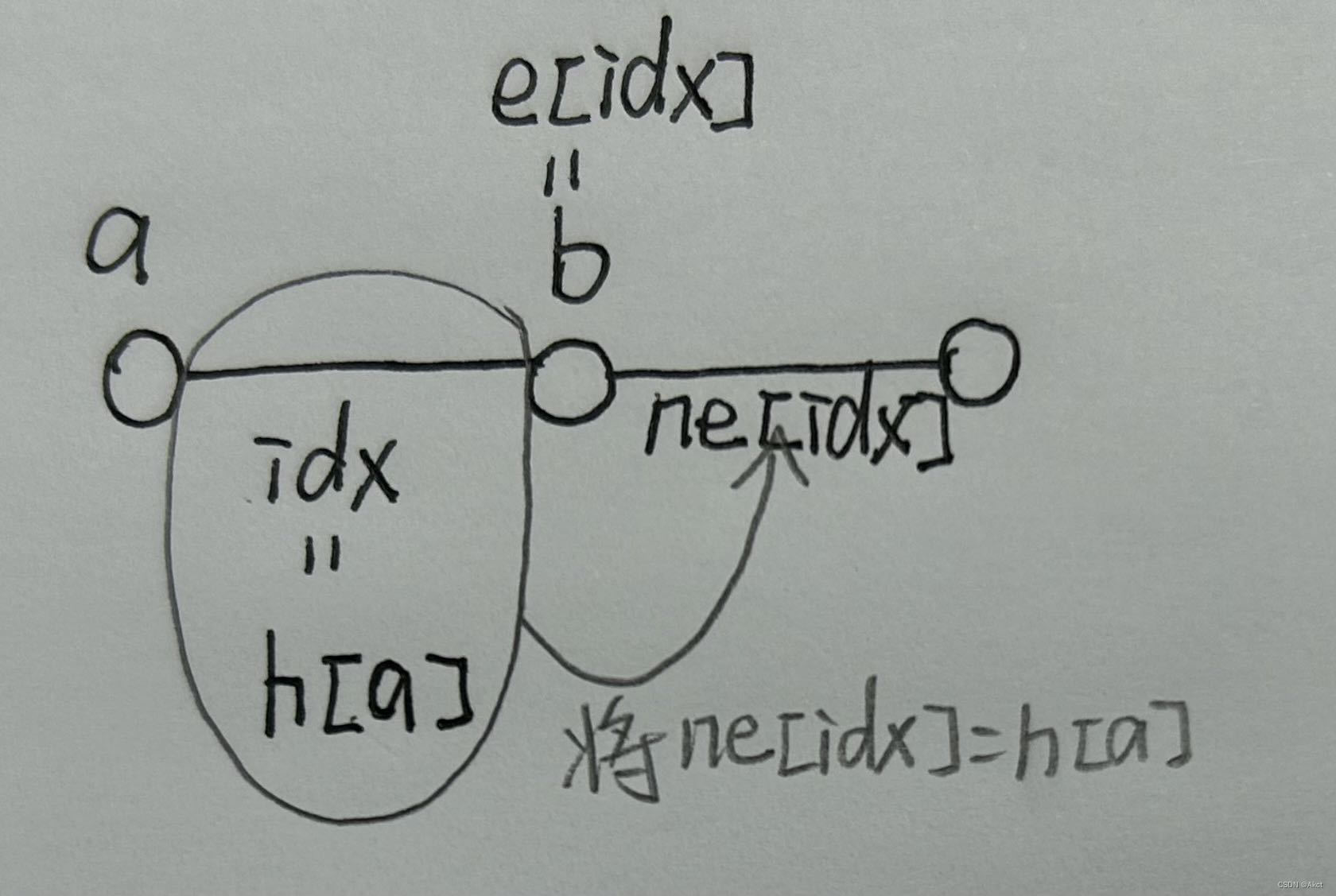
	e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
int dijkstra()
{
	memset(d, 0x3f, sizeof d);
	d[1] = 0;
	priority_queue<PII, vector<PII>, greater<PII>> q;
	q.push({0, 1});
	while(q.size())
	{
		auto t = q.top();
		q.pop();
		int num = t.second, dis = t.first;
		if(st[num])continue;
		st[num] = true;
		for(int i = h[num]; i != -1; i = ne[i])
		{
			int j = e[i];
			if(d[j] > dis + w[i])
			{
				d[j] = dis + w[i];
				q.push({d[j], j});
			}
		}
	}
	//if(d[2021] == 0x3f3f3f3f)return -1;
	return d[2021];
} 
int main()
{	
	memset(h, -1, sizeof h);
	for(int i = 1; i <= 2021; i ++)
	{
		for(int j = 1; j <= 2021; j ++)
		{
			if(abs(i - j) <= 21)
			{
				add(i, j, lcm(i, j));
			}
		}
	}
	cout << dijkstra();
	return 0;
}