参考 $B$ 题做法…

class Solution {
public:
    using ll = long long;

    long long maximumTripletValue(vector<int> &nums) {
        int n = nums.size();
        vector<int> suf(n);
        partial_sum(nums.rbegin(), nums.rend(), suf.rbegin(), [](int x, int y) { return max(x, y); });
        ll res = 0;
        for (int mx = nums[0], j = 1; j < n - 1; j++) {
            if (mx > nums[j])
                res = max(res, 1LL * (mx - nums[j]) * suf[j + 1]);
            mx = max(mx, nums[j]);
        }
        return res;
    }
};

枚举：预处理求出 p r e [ j − 1 ] = m a x { n u m s [ k ]    ∣    0 < k < j } pre[j-1]=max\{ nums[k] \; | \; 0<k<j \} pre[j−1]=max{nums[k]∣0<k<j} 和 s u f [ j + 1 ] = m a x { n u m s [ k ]    ∣    j < k < n u m s . s i z e ( ) } suf[j+1]=max\{ nums[k] \;| \; j<k<nums.size() \} suf[j+1]=max{nums[k]∣j<k<nums.size()}，枚举下标 $j$ ，则三元组中间位置为 $j$ 的三元组的最大值为 $(pre[j-1]-nums[j])\times suf[j+1]$

class Solution {
public:
    using ll = long long;

    long long maximumTripletValue(vector<int> &nums) {
        int n = nums.size();
        vector<int> suf(n);//最大值后缀数组
        partial_sum(nums.rbegin(), nums.rend(), suf.rbegin(), [](int x, int y) { return max(x, y); });
        ll res = 0;
        for (int mx = nums[0], j = 1; j < n - 1; j++) {//mx即为pre[j-1]
            if (mx > nums[j])
                res = max(res, 1LL * (mx - nums[j]) * suf[j + 1]);
            mx = max(mx, nums[j]);
        }
        return res;
    }
};

双指针：设数组元素和为 $s$ ，若 $target\%s==0$，则答案为 $\frac{target}{s}\times nums.size()$，否则问题可以转化为：在数组中找一个子数组或一个前缀加一个后缀，使得找到的元素数尽量少且元素和为 $target\%s$。

class Solution {
public:
    using ll = long long;

    int minSizeSubarray(vector<int> &nums, int target) {
        ll s = accumulate(nums.begin(), nums.end(), 0LL);
        int n = nums.size();
        int res0 = target / s * n;//覆盖完整数组的元素数
        target %= s;
        if (target == 0)
            return res0;
        vector<ll> pre(n), suf(n);//pre:前缀和数组, suf:后缀和数组
        partial_sum(nums.begin(), nums.end(), pre.begin(), [](int x, int y) { return (ll) x + (ll) y; });
        partial_sum(nums.rbegin(), nums.rend(), suf.rbegin(), [](int x, int y) { return (ll) x + (ll) y; });
        int res1 = INT32_MAX;
        for (int l = 0, r = 0; l < n; l++) {//一个前缀加一个后缀的情况
            while (r + 1 < n && pre[l] + suf[r + 1] >= target)
                r++;
            if (pre[l] + suf[r] == target)
                res1 = min(res1, l + 1 + n - r);
        }
        for (int l = 0, r = 0; r < n; r++) {//子数组的情况
            while (l + 1 <= r && pre[r] - pre[l] >= target)
                l++;
            if ((l != 0 ? pre[r] - pre[l - 1] : pre[r]) == target)
                res1 = min(res1, r - l + 1);
        }
        return res1 == INT32_MAX ? -1 : res0 + res1;
    }
};

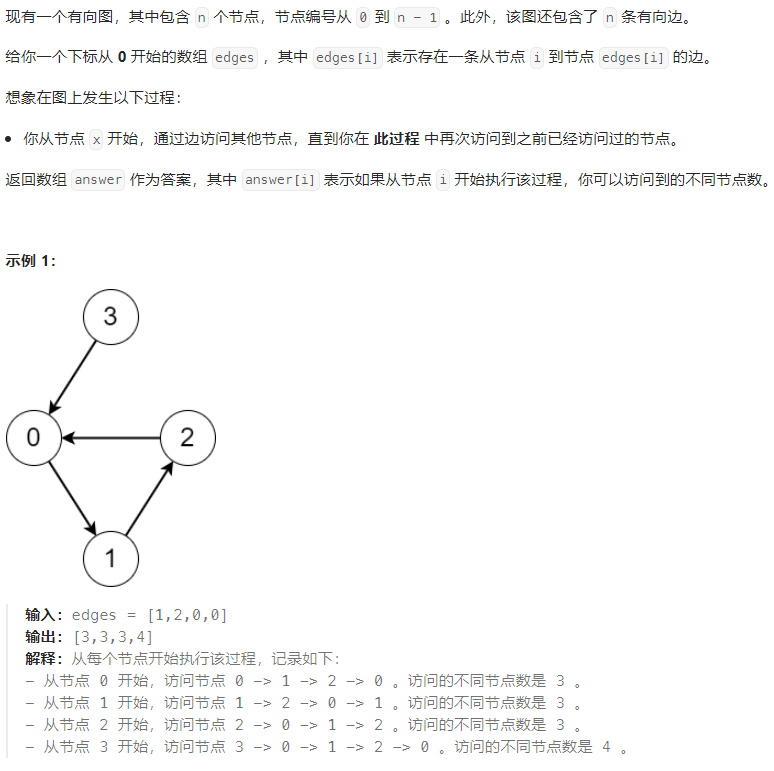
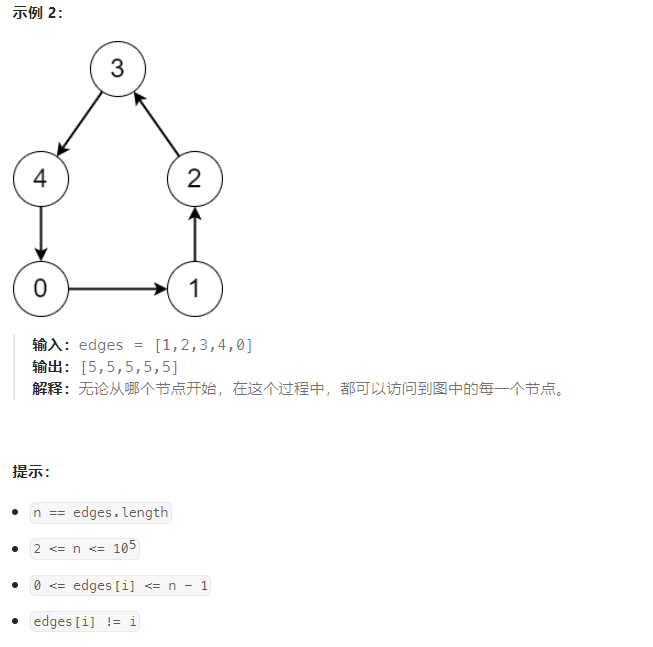
拓扑排序+ $dfs$ ：所述有向图对应的无向图中每个连通分支一定是一个环加若干链的结构，一个点能访问的节点总数为：该点在无向图中所属连通分支的环的大小+该点到环上节点的最小距离。通过拓扑排序求出哪些节点在环上，然后可以求出每个环的大小，再从环上的节点在反向图上跑 $dfs$ ，求出对应链上节点与环上节点的最小距离。

class Solution {
public:
    vector<int> countVisitedNodes(vector<int> &edges) {
        int n = edges.size();
        vector<vector<int>> e_(n);//反向图的邻接表
        vector<int> indegree(n);//入度
        for (int i = 0; i < n; i++) {
            indegree[edges[i]]++;
            e_[edges[i]].push_back(i);
        }
        queue<int> q;
        for (int i = 0; i < n; i++)
            if (!indegree[i])
                q.push(i);
        vector<int> is_out(n);//是否在环外
        while (!q.empty()) {//拓扑排序求出环外的点
            int cur = q.front();
            q.pop();
            is_out[cur] = 1;
            if (--indegree[edges[cur]] == 0)
                q.push(edges[cur]);
        }
        vector<int> size_ring(n, -1);//各节点所在环的大小
        for (int i = 0; i < n; i++)//计算各个环的大小
            if (!is_out[i] && size_ring[i] == -1) {//-1为初始化标志(一个环只用遍历一次)
                int m = 0;
                for (int cur = i;;) {
                    m++;
                    cur = edges[cur];
                    if (cur == i)
                        break;
                }
                for (int cur = i;;) {
                    size_ring[cur] = m;
                    cur = edges[cur];
                    if (cur == i)
                        break;
                }
            }
        vector<int> res(n);
        function<void(int, int, int)> dfs = [&](int cur, int dis, int len_ring) {//cur: 当前节点, dis: 距离环中节点的最小距离, len_ring: 环的大小
            res[cur] = dis + len_ring;
            for (auto j: e_[cur])
                if (is_out[j])
                    dfs(j, dis + 1, len_ring);
        };
        for (int i = 0; i < n; i++)
            if (!is_out[i])
                dfs(i, 0, size_ring[i]);
        return res;
    }
};