[NOIP2011 提高组] 选择客栈

题目描述

丽江河边有 $n$ 家很有特色的客栈，客栈按照其位置顺序从 $1$ 到 $n$ 编号。每家客栈都按照某一种色调进行装饰（总共 $k$ 种，用整数 $0\sim k-1$ 表示），且每家客栈都设有一家咖啡店，每家咖啡店均有各自的最低消费。

两位游客一起去丽江旅游，他们喜欢相同的色调，又想尝试两个不同的客栈，因此决定分别住在色调相同的两家客栈中。晚上，他们打算选择一家咖啡店喝咖啡，要求咖啡店位于两人住的两家客栈之间（包括他们住的客栈），且咖啡店的最低消费不超过 $p$ 。

他们想知道总共有多少种选择住宿的方案，保证晚上可以找到一家最低消费不超过 $p$ 元的咖啡店小聚。

输入格式

共 $n+1$ 行。

第一行三个整数 $n,k,p$，每两个整数之间用一个空格隔开，分别表示客栈的个数，色调的数目和能接受的最低消费的最高值；

接下来的 $n$ 行，第 $i+1$ 行两个整数，之间用一个空格隔开，分别表示 $i $ 号客栈的装饰色调 $a_i$ 和 $i$ 号客栈的咖啡店的最低消费 $b_i$。

输出格式

一个整数，表示可选的住宿方案的总数。

样例 #1

样例输入 #1

5 2 3 
0 5 
1 3 
0 2 
1 4 
1 5

样例输出 #1

3

提示

样例解释

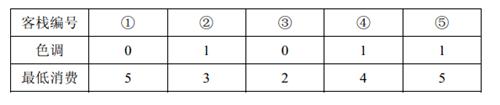
2 人要住同样色调的客栈，所有可选的住宿方案包括：住客栈①③，②④，②⑤，④⑤，但是若选择住 $4,5$号客栈的话，$4,5$ 号客栈之间的咖啡店的最低消费是 $4$ ，而两人能承受的最低消费是 $3$ 元，所以不满足要求。因此只有前 $3$ 种方案可选。

数据范围

• 对于 $30% $ 的数据，有 $n\le 100$ ；
• 对于 $50% $ 的数据，有 $n\le 1000$；
• 对于 $100\%$ 的数据，有 $2\le n\le 2\times 10^5$，$1\le k\le 50$，$0\le p\le 100$，$0\le b_i\le 100$。

大致思路

change[i]存的是i色调客栈距离前一个能够满足p要求的客栈中间隔了多少个待机（也就是不满足要求）的客栈

而sum[i]存的是i色调客栈之前的客栈能够满足要求的客栈总数，（具体做法是和DRJ大佬出校门的时候想到的）

边输入边处理，当到i的时候，如果i之前有个客栈的消费满足小于p，那么这个客栈之前的所有客栈都可以和这个i进行一次匹配，而怎么得到之前满足的数目呢，这时候就要看看i本身怎么处理。

1.如果i本身满足要求小于p，那么就说明i之前的所有待机的客栈在接下来的i-n客栈中都可以匹配一次，所以一次for循环，把change[j]加到sum[j]中去，接下来ans再加一次sum[color]全部匹配一次。

2.如果i本身不满足的话，那么同样要进行一次ans+sum[color]，原因的话看懂了1就明白了。它不满足，如果接下来的i+1-n客栈中没有一个消费满足小于p的消费，那么是不是说明现在的这个i客栈对接下来的客栈一点贡献都没有了？所以把它放到change数组，change[color]++，如果接下来能够碰上为它搭桥（就是满足最低消费小于p）的客栈就把它放到sum，让它能够对接下来的客栈ans做贡献。

最后直接输出ans，愉快的AC

#include<bits/stdc++.h>
using namespace std;
int change[55], sum[55], ans, n, k, p;
int main()
{
    scanf("%d%d%d", &n, &k, &p);
    for(int i = 1; i <= n; ++i){
        int color, cos;
        scanf("%d%d", &color, &cos);
        if(cos <= p){
            for(int j = 0; j <= 50; ++j)
                if(change[j]){sum[j]+=change[j];change[j] = 0;}
            ans += sum[color];
            sum[color]++;
        }
        else
        change[color]++, ans += sum[color];
    }
    printf("%d", ans);
    return 0;
}

封面