Javaweb作业小结
news2026/2/14 13:00:23
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1054412.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
动态规划:两个数组的dp问题(C++)
动态规划:两个数组的dp问题 前言两个数组的dp问题1.最长公共子序列(中等)2.不同的子序列(困难)3.通配符匹配(困难)4.正则表达式(困难)5.交错字符串(中等&…
Go结构体深度探索:从基础到应用
在Go语言中,结构体是核心的数据组织工具,提供了灵活的手段来处理复杂数据。本文深入探讨了结构体的定义、类型、字面量表示和使用方法,旨在为读者呈现Go结构体的全面视角。通过结构体,开发者可以实现更加模块化、高效的代码设计。…
JavaSE学习之--抽象类和接口
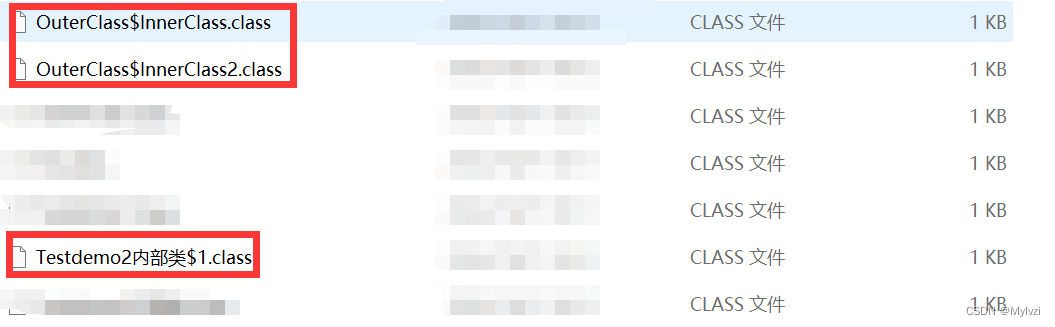
💕"没有眼泪我们就会迷路,彻底变成石头,我们的心会变成冰凌,吻会变成冰块。"💕 作者:Mylvzi 文章主要内容:JavaSE学习之--抽象类和接口 一.抽象类
1.抽象类的定义 我们知道&#x…
数仓精品理论-做大数据还有没有前途?
数仓精品理论-做大数据还有没有前途? 做大数据还有没有前途?大数据三要三不要我来讲讲大数据前景 做大数据还有没有前途? 先说,答案是肯定的,但一定要记住三要三不要。 datapulse官网: github:https://data…
cesium gltf控制
gltf格式详解
glTF格式本质上是一个JSON文件。这一文件描述了整个3D场景的内容。它包含了对场景结构进行描述的场景图。场景中的3D对象通过场景结点引用网格进行定义。材质定义了3D对象的外观,动画定义了3D对象的变换操作(比如选择、平移操作)。蒙皮定义了3D对象如何进行骨骼…
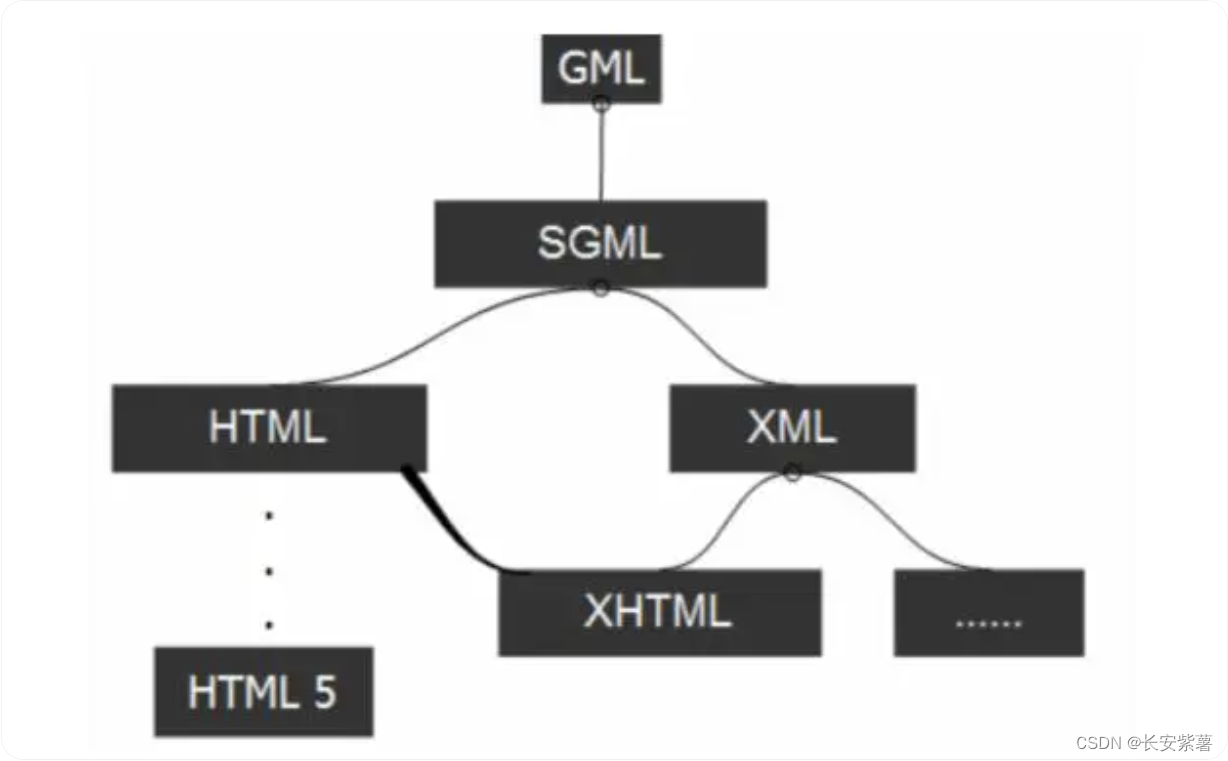
黑豹程序员-架构师学习路线图-百科:HTML-网页三剑客
为什么需要HTML
在网站技术发达之前,千年来我们获取信息是通过书籍。电脑流行后我们看文章、小说通过txt文件。看图通过单独的图片流量工具看单个的图片文件。
而HTML把文字和图片一起展示,让今天的电子书成为可能。
另外一点,我们的信息是…
【操作系统】了解Linux操作系统中PCB进程管理模块与进程PID
本篇要分享的内容是有关于操作系统中进程的内容。
目录
1.进程的简单理解
2.了解task_struct(进程控制模块)内容分类
3.task_struct(进程控制模块)中的PID
4.调用查看PID的函数 1.进程的简单理解
首先我们需要理解的是什么是…
简单讲解 glm::mat4
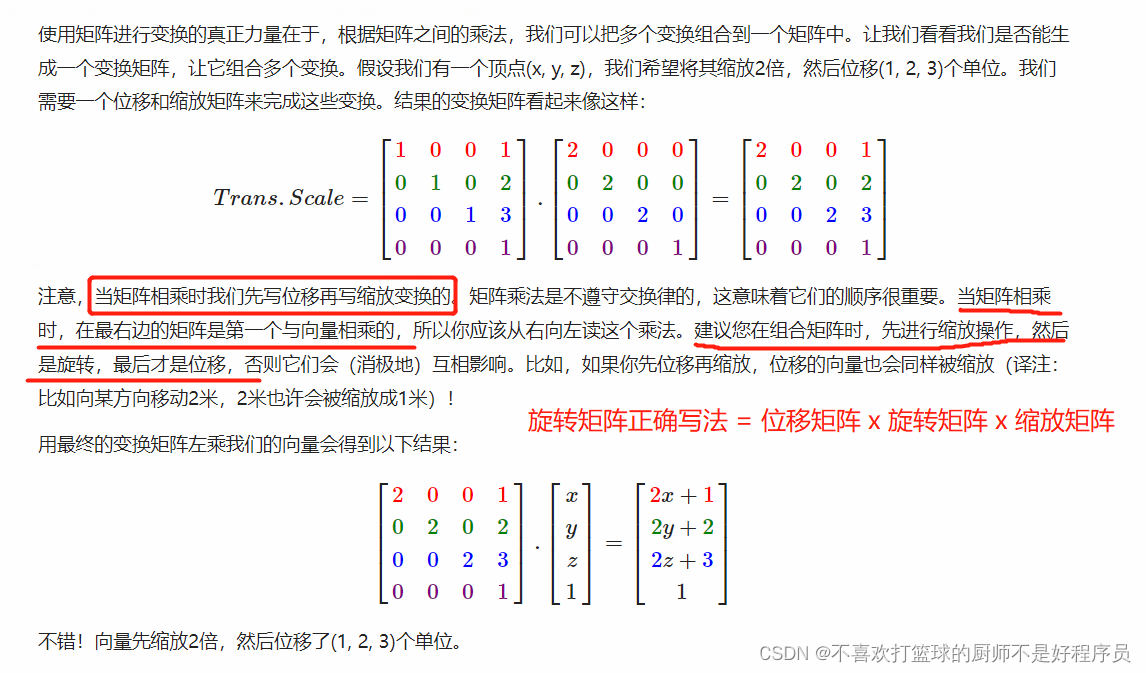
文章目录 前言一、下载glm库二、基本数学知识1. 三维中的 4 x 4 矩阵2.旋转3. 位移4. 缩放5. 组合 三、行向量或列向量四、总结 前言
glm库是OpenGL的官方数学库,里面内置多种跟几何变换相关的函数,熟练掌握glm库可以省下很多麻烦。 因为最近在项目中主…
鞋类 整鞋试验方法 剥离强度
声明
本文是学习GB-T 3903.3-2011 鞋类 整鞋试验方法 剥离强度. 而整理的学习笔记,分享出来希望更多人受益,如果存在侵权请及时联系我们
1 范围
GB/T 3903 的本部分规定了整鞋鞋底与鞋帮或外底与外中底之间剥离强度的试验方法。
本部分适用于采用模压、硫化、注塑、灌注、胶…
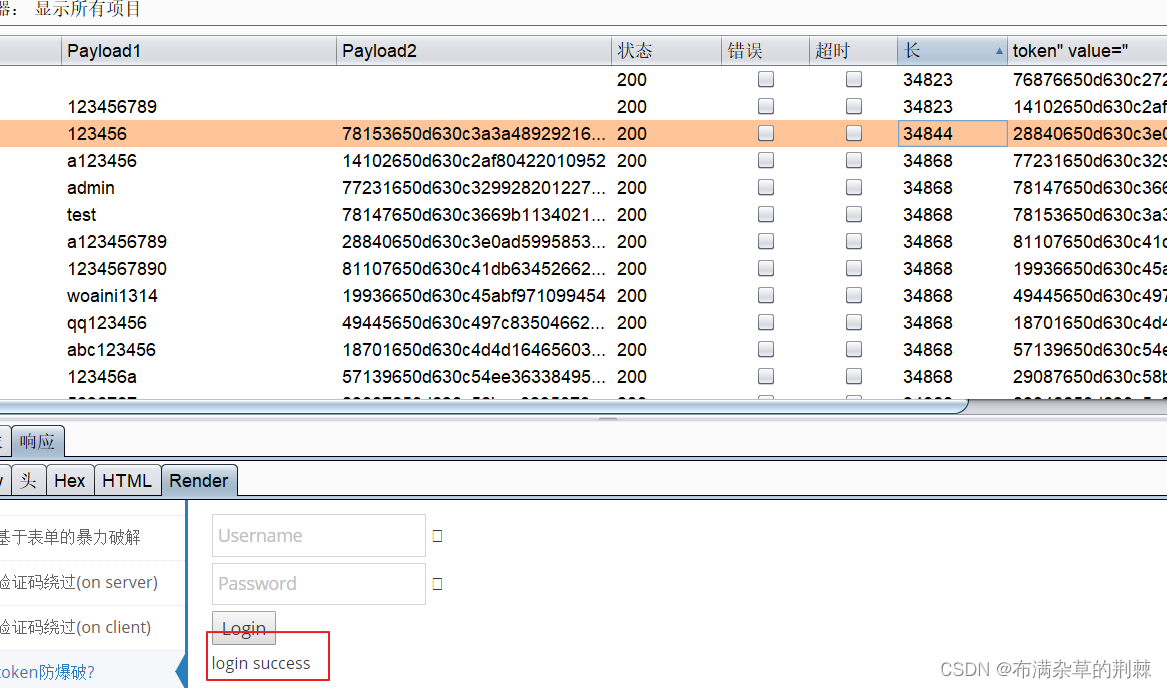
暴力破解及验证码安全
1.暴力破解注意事项 1、破解前一定要有一个有郊的字典(Top100 TOP2000 csdn QQ 163等密码) https://www.bugku.com/mima/ 密码生成器 2、判断用户是否设置了复杂的密码 在注册页面注册一个,用简单密码看是否可以注册成功 3、网站是…
Jenkins集成AppScan实现
一、Jenkins上安装插件 在Jenkins里安装以下插件
ibm-security-appscanstandard-scanner 二、打开AppScan 1、配置需要扫描的地址 配置需要扫描的地址 2、记录好要扫描的URL登录序列 记录好要扫描的URL登录序列 3、导出要扫描的URL登录序列设置 导出要扫描的URL登录序列设置 三…
C程序设计内容与例题讲解 -- 第四章--选择结构程序设计(第五版)谭浩强
前言:在第三章我们介绍了顺序结构程序设计。在顺序结构中,各个语句是按自上而下的顺序执行的,执行完上一个语句就自动执行下一个语句,是无条件的,不必做任何判断。是这最简单的程序结构。实际上,在很多情况…
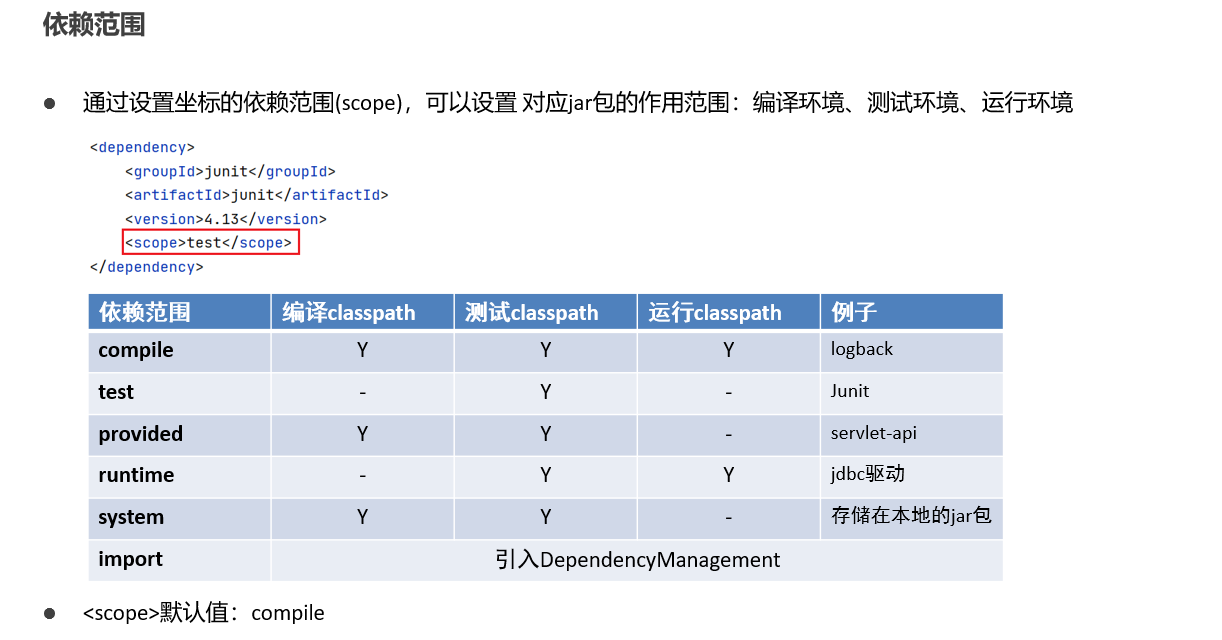
IDEA 配置 Maven(解决依赖下载缓慢)
IDEA 配置 Maven(解决依赖下载缓慢) 这一篇主要介绍 Maven 的基本用法。等我之后学习到框架知识时,会完善此部分内容。 一、Maven 简介 Maven 是专门用于管理和构建 Java 项目的工具,Apache Maven 是一个项目管理和构建工具&#…
ali内核服务器搭建Linux版本的小皮面板(微调)
一、搭建小皮面板
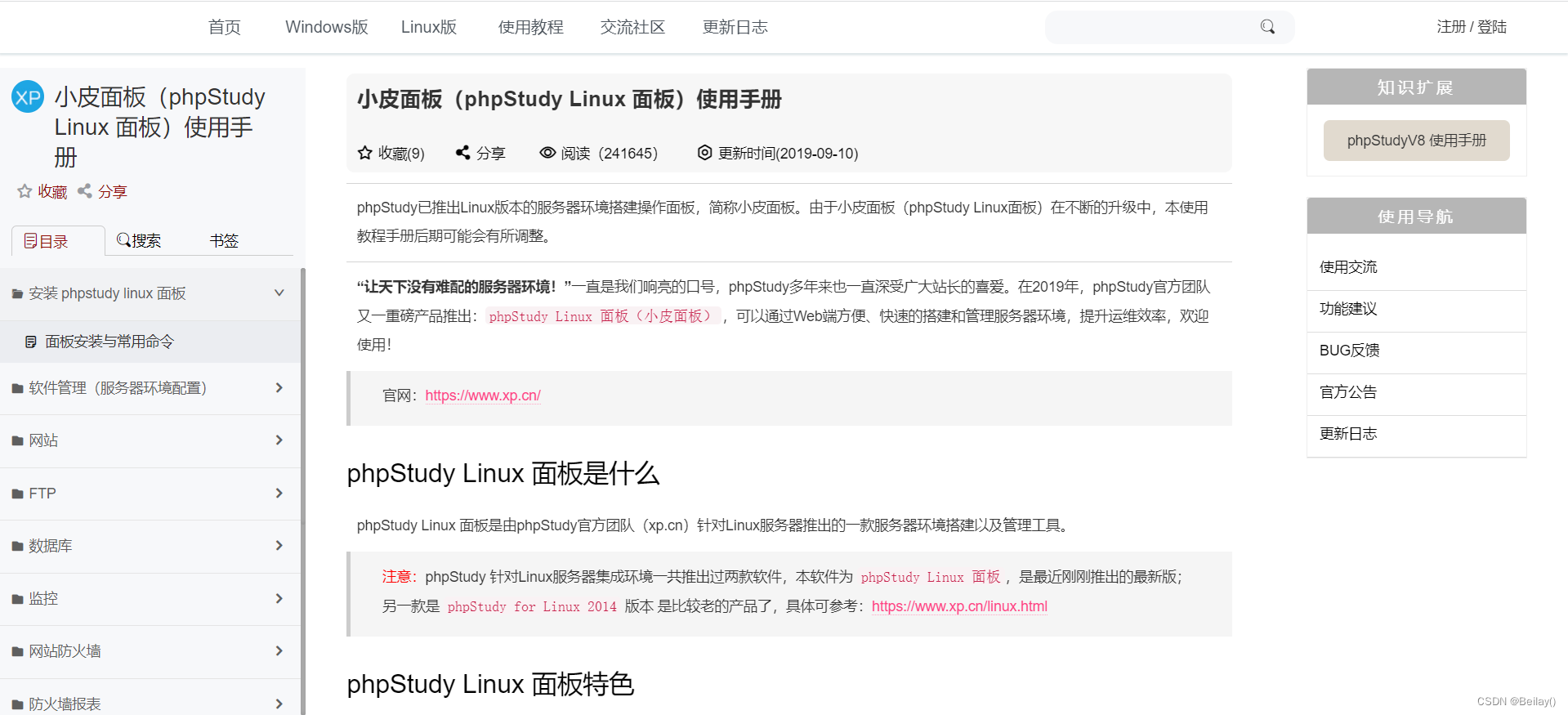
windows版本的小皮面板我们经常使用,早就熟悉了搭建和配置 那么这里我们就来使用Linux版本的小皮面板,看看如何进行操作
安装网址: https://www.xp.cn/linux.html
这里根据自己的操作系统选择合适的命令 我使用的是kali搭建,因此选择Debian安装脚本
注意:…
28270-2012 智能型阀门电动装置 学习笔记
声明
本文是学习GB-T 28270-2012 智能型阀门电动装置. 而整理的学习笔记,分享出来希望更多人受益,如果存在侵权请及时联系我们
1 范围
本标准规定了智能型阀门电动装置(以下简称智能电装)的术语、技术要求、试验方法、检验规则、标
志、包装、运输和贮存条件等。
本标准适…
MATLAB与Python:优势与挑战
本文旨在探讨MATLAB与Python在特定领域内的使用情况,并分析两者之间的优势和挑战。
MATLAB和Python都是流行的编程语言,广泛应用于科学计算、数据分析和机器学习等领域。在某些领域,如航空航天工程、自动化和电子工程嵌入式系统开发等&#…