背包问题

news2024/11/23 9:38:14

目录

开端

01背包问题

AcWing 01背包问题

Luogu P2925干草出售

Luogu P1048采药

完全背包问题

AcWing 完全背包问题

Luogu P1853投资的最大效益

多重背包问题

AcWing 多重背包问题 I

AcWing 多重背包问题 II

Luogu P1776宝物筛选

混合背包问题

AcWing 混合背包问题

Luogu P1833樱花

二维费用背包问题

AcWing 二维费用的背包问题 

Luogu P1507NASA的食物计划

分组背包问题

AcWing 分组背包问题

Luogu P1757 通天之分组背包

开端

关于背包问题，嗯一直学不明白，暑假咸的没事又拾起来学了一下，跟着这位大佬整理的思路（背包九讲——全篇详细理解与代码实现-CSDN博客），对背包的思想有了一定清晰的理解，大佬的文章有些长，所以跟着自己的思路再整理一下。

为了方便统一，先定义一下

c[i]：表示代价

w[i]：表示价值

dp[i][j]：表示前i个物品花费代价为j的可以获得的最大代价

p[i]：表示第i种物品最多有p[i]件

01背包问题

定义：

dp[i][j]：表示前i个物品恰放入一个容量为j的背包下可以获得的最大代价

子问题第i1件物品状态：

①不选：dp[i][j]=dp[i-1][j]

②选：dp[i][j]=dp[i][j-c[i]]+w[i]

状态转移方程：

dp[i][j]=max(dp[i-1][j],dp[i][j-c[i]]+w[i])

优化空间复杂度：

O(V*N)

for(int i=1;i<=n;i++)
    for(int j=c[i];j<=V;j--)
        dp[i][j]=max(dp[i-1][j],dp[i-1][j-c[i]]+w[i]);

O(V)

for(int i=1;i<=n;i++)
    for(int j=V;j>=c[i];j++)
        dp[j]=max(dp[j],dp[j-c[i]]+w[i]);

关于顺序和逆序：

逆序表示：dp[j]=max(dp[j],dp[j-c[i]]+w[i])由dp[i][j]=max(dp[i-1][j],dp[i-1][j-c[i]]+w[i])转移过来的
顺序表示：dp[j]=max(dp[j],dp[j-c[i]]+w[i])由dp[i][j]=max(dp[i][j],dp[i][j-c[i]]+w[i])转移过来的

初始化问题：

①要求恰好装满：dp[i]=-∞,dp[0]=0;

②只要求价值最大：dp[i]=0;

 AcWing 01背包问题

const int N = 1010;
int c[N], w[N], dp[N];
inline void solve()
{
    int N, V;
    cin >> N >> V;
    for (int i = 1; i <= N; i++)
        cin >> c[i] >> w[i];
    for (int i = 1; i <= N; i++)
        for (int j = V; j >= c[i]; j--)
            dp[j] = max(dp[j], dp[j - c[i]] + w[i]);
    cout << dp[V] << endl;
}

Luogu P2925干草出售

const int N = 5e4 + 10;
int w[N], dp[N];
inline void solve()
{
    int C, H;
    cin >> C >> H;
    for (int i = 1; i <= H; i++)
        cin >> w[i];
    for (int i = 1; i <= H; i++)
        for (int j = C; j >= w[i]; j--)
            dp[j] = max(dp[j], dp[j - w[i]] + w[i]);
    cout << dp[C] << endl;
}

Luogu P1048采药

const int N = 1010;
int c[N], w[N], dp[N];
inline void solve()
{
    int T, M;
    cin >> T >> M;
    for (int i = 1; i <= M; i++)
        cin >> c[i] >> w[i];
    for (int i = 1; i <= M; i++)
        for (int j = T; j >= c[i]; j--)
            dp[j] = max(dp[j], dp[j - c[i]] + w[i]);
    cout << dp[T] << endl;
}

完全背包问题

 定义：

dp[i][j]：表示前i种物品恰放入一个容量为j的背包下可以获得的最大代价

子问题第i种物品状态：

①不选该种物品：dp[i][j]=dp[i-1][j];
②选不同件该种物品：选0件、1件、2件……k件：dp[i][j]=dp[i-1][j-c[i]*k]+w[i]*k;

状态转移方程：

dp[i][j]=max(dp[i-1][j-c[i]*k]+w[i]*k)  0<=c[i]*k<=j

优化空间复杂度：

O(N*∑(V/c[i]))

for(int i=1;i<=n;i++)
    for(int j=c[i];j<=V;j++)
        for(int k=0;c[i]*k<=j;k++)
            dp[i][j]=max(dp[i][j],dp[i-1][j-c[i]*k]+w[i]*k);
# 第一个参数，因为k=0时就相当于dp[i-1][j];

O(V*N)转化为01背包问题

for(int i=1;i<=n;i++)
    for(int j=c[i];j<=j;j++)
        dp[j]=max(dp[j],dp[j-c[i]]+w[i]);
//等价于dp[i][j]=max(dp[i-1][j],dp[i][j-c[i]]+w[i]);(不取该物品，取不同件)；

关于顺序和逆序：

逆序表示：dp[j]=max(dp[j],dp[j-c[i]]+w[i])由dp[i][j]=max(dp[i-1][j],dp[i-1][j-c[i]]+w[i])转移过来的
顺序表示：dp[j]=max(dp[j],dp[j-c[i]]+w[i])由dp[i][j]=max(dp[i-1][j],dp[i][j-c[i]]+w[i])转移过来的

初始化问题：

①要求恰好装满：dp[i]=-∞,dp[0]=0;

②只要求价值最大：dp[i]=0;

AcWing 完全背包问题

const int N = 1010;
int c[N], w[N], dp[N];
inline void solve()
{
    int N, V;
    cin >> N >> V;
    for (int i = 1; i <= N; i++)
        cin >> c[i] >> w[i];
    for (int i = 1; i <= N; i++)
        for (int j = c[i]; j <= V; j++)
            dp[j] = max(dp[j], dp[j - c[i]] + w[i]);
    cout << dp[V] << endl;
}

Luogu P1853投资的最大效益

const int N = 1e6 + 10;
int c[N], w[N], dp[N];
inline void solve()
{
    int s, n, d;
    cin >> s >> n >> d;
    for (int i = 1; i <= d; i++)
        cin >> c[i] >> w[i];
    while (n--)
    {
        for (int i = 1; i <= d; i++)
            for (int j = c[i]; j <= s; j++)
                dp[j] = max(dp[j], dp[j - c[i]] + w[i]);
        s += dp[s];
    }
    cout << s << endl;
}
int main(

这个题目有个小坑

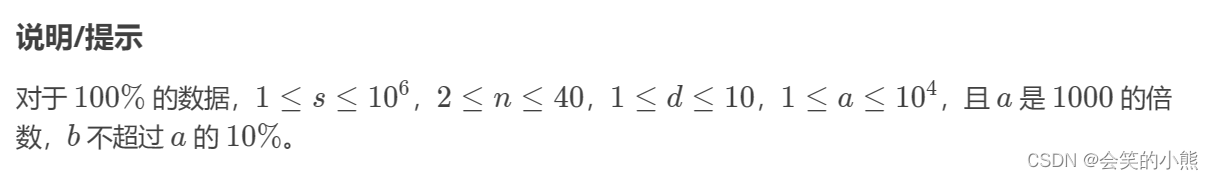
所以要做一下处理：除以1000防止爆空间

const int N = 1e6 + 10;
int c[N], w[N], dp[N];
inline void solve()
{
    int s, n, d;
    cin >> s >> n >> d;
    for (int i = 1; i <= d; i++)
        cin >> c[i] >> w[i];
    while (n--)
    {
        for (int i = 1; i <= d; i++)
            for (int j = c[i] / 1000; j <= s / 1000; j++)
                dp[j] = max(dp[j], dp[j - c[i] / 1000] + w[i]);
        s += dp[s / 1000];
    }
    cout << s << endl;
}

多重背包问题

  定义：

dp[i][j]：表示前i种物品恰放入一个容量为j的背包下可以获得的最大代价

子问题第i种物品状态：

①不选该种物品：dp[i][j]=dp[i-1][j];
②选不同件该种物品：选1件、2件……p[i]件：dp[i][j]=dp[i-1][j-c[i]*k]+w[i]*k;

状态转移方程：

dp[i][j]=max(dp[i-1][j-c[i]*k]+w[i]*k)  0<=k<=p[i]

转化为01背包问题：

方法一：O(V*∑p[i])

for(int i=1;i<=n;i++)
    for(int j=V;j>=c[i];j--)
        for(int k=1;c[i]*k<=j&&k<=p[i];k++)
            dp[j]=max(dp[j],dp[j-c[i]*k]+w[i]*k);
# 第一个参数，因为k=0时就相当于dp[i-1][j];

方法二：二进制优化O(N*log(p)*V)

for (int i = 1; i <= N; i++)
    {
        int a, b, s;
        cin >> a >> b >> s;
        int k = 1;
        while (k <= s)  //0……2^k-1部分的系数1，2，4，8……
        {
            cnt++;
            c[cnt] = k * a;
            w[cnt] = k * b;
            s -= k;
            k *= 2;
        }
        if (s > 0)  //2^k……s部分的系数 s-2^k
        {
            cnt++;
            c[cnt] = s * a;
            w[cnt] = s * b;
        }
    }
    N = cnt;  //更新总数量
    for (int i = 1; i <= N; i++)  //01背包问题
        for (int j = V; j >= c[i]; j--)
            dp[j] = max(dp[j], dp[j - c[i]] + w[i]);
 for (int i = 1; i <= n; i++)
    {
        cin >> c[i] >> w[i] >> p[i];
        int s = min(p[i], W / w[i]);
        for (int k = 1; s > 0; k <<= 1)
        {
            k = min(k, s);
            s -= k;
            for (int j = W; j >= k * w[i]; j--)
            {
                dp[j] = max(dp[j], dp[j - k * w[i]] + k * c[i]);
            }
        }
    }

初始化问题：

①要求恰好装满：dp[i]=-∞,dp[0]=0;

②只要求价值最大：dp[i]=0;

方法一：

AcWing 多重背包问题 I

const int N = 110;
int c[N], w[N], p[N], dp[N];
inline void solve()
{
    int N, V;
    cin >> N >> V;
    int cnt = 0;
    for (int i = 1; i <= N; i++)
        cin >> c[i] >> w[i] >> p[i];
    for (int i = 1; i <= N; i++)
        for (int j = V; j >= c[i]; j--)
            for (int k = 1; c[i] * k <= j && k <= p[i]; k++)
                dp[j] = max(dp[j], dp[j - c[i] * k] + w[i] * k);
    cout << dp[V] << endl;
}

方法二：

AcWing 多重背包问题 II

const int N = 20010;  //注意初始化，否则会越界
int c[N], w[N], dp[N];
inline void solve()
{
    int N, V;
    cin >> N >> V;
    int cnt = 0;
    for (int i = 1; i <= N; i++)
    {
        int a, b, s;
        cin >> a >> b >> s;
        int k = 1;
        while (k <= s)  //0……2^k-1部分的系数1，2，4，8……
        {
            cnt++;
            c[cnt] = k * a;
            w[cnt] = k * b;
            s -= k;
            k *= 2;
        }
        if (s > 0)  //2^k……s部分的系数 s-2^k
        {
            cnt++;
            c[cnt] = s * a;
            w[cnt] = s * b;
        }
    }
    N = cnt;  //更新总数量
    for (int i = 1; i <= N; i++)  //01背包问题
        for (int j = V; j >= c[i]; j--)
            dp[j] = max(dp[j], dp[j - c[i]] + w[i]);
    cout << dp[V] << endl;
}

Luogu P1776宝物筛选

const int N = 1e6 + 10; // 注意初始化，否则会越界
int c[N], w[N], dp[N];
inline void solve()
{
    int n, W;
    cin >> n >> W;
    int cnt = 0;
    for (int i = 1; i <= n; i++)
    {
        int a, b, s;
        cin >> a >> b >> s;
        int k = 1;
        while (k <= s)
        {
            cnt++;
            w[cnt] = k * a;
            c[cnt] = k * b;
            s -= k;
            k *= 2;
        }
        if (s > 0)
        {
            cnt++;
            w[cnt] = s * a;
            c[cnt] = s * b;
        }
    }
    n = cnt;
    for (int i = 1; i <= n; i++)
        for (int j = W; j >= c[i]; j--)
            dp[j] = max(dp[j], dp[j - c[i]] + w[i]);
    cout << dp[W] << endl;
}

简化

const int N = 1e6 + 10; // 注意初始化，否则会越界
int c[N], w[N], p[N], dp[N];
inline void solve()
{
    int n, W;
    cin >> n >> W;
    for (int i = 1; i <= n; i++)
    {
        cin >> c[i] >> w[i] >> p[i];
        int s = min(p[i], W / w[i]);
        for (int k = 1; s > 0; k <<= 1)
        {
            k = min(k, s);
            s -= k;
            for (int j = W; j >= k * w[i]; j--)
            {
                dp[j] = max(dp[j], dp[j - k * w[i]] + k * c[i]);
            }
        }
    }
    cout << dp[W] << endl;
}

混合背包问题

 01背包、完全背包、多重背包的混合状态转移：

for (int i = 1; i <= N; i++)
    {
        cin >> c[i] >> w[i] >> p[i];
        // 01背包
        if (p[i] == -1)
            for (int j = V; j >= c[i]; j--)
                dp[j] = max(dp[j], dp[j - c[i]] + w[i]);
        // 完全背包
        else if (p[i] == 0)
            for (int j = c[i]; j <= V; j++)
                dp[j] = max(dp[j], dp[j - c[i]] + w[i]);
        // 多重背包二进制优化
        else
        {
            int s = min(p[i], V / c[i]);
            for (int k = 1; s > 0; k <<= 1)
            {
                k = max(k, s);
                s -= k;
                for (int j = V; j >= k * c[i]; j--)
                    dp[j] = max(dp[j], dp[j - k * c[i]] + k * w[i]);
            }
        }
    }

AcWing 混合背包问题

const int N = 1e6 + 10; // 注意初始化，否则会越界
int c[N], w[N], p[N], dp[N];
inline void solve()
{
    int N, V;
    cin >> N >> V;
    for (int i = 1; i <= N; i++)
    {
        cin >> c[i] >> w[i] >> p[i];
        // 01背包
        if (p[i] == -1)
            for (int j = V; j >= c[i]; j--)
                dp[j] = max(dp[j], dp[j - c[i]] + w[i]);
        // 完全背包
        else if (p[i] == 0)
            for (int j = c[i]; j <= V; j++)
                dp[j] = max(dp[j], dp[j - c[i]] + w[i]);//或将完全背包转化为多重01背包s=V/c[i]
        // 多重背包二进制优化
        else
        {
            int s = min(p[i], V / c[i]);
            for (int k = 1; s > 0; k <<= 1)
            {
                k = min(k, s);
                s -= k;
                for (int j = V; j >= k * c[i]; j--)
                    dp[j] = max(dp[j], dp[j - k * c[i]] + k * w[i]);
            }
        }
    }
    cout << dp[V] << endl;
}

Luogu P1833樱花

const int N = 1e6 + 10; // 注意初始化，否则会越界
int c[N], w[N], p[N], dp[N];
inline void solve()
{
    int m1, m2, s1, s2, N;
    scanf("%d:%d %d:%d %d", &m1, &s1, &m2, &s2, &N);
    int V = m2 * 60 + s2 - m1 * 60 - s1;
    for (int i = 1; i <= N; i++)
    {
        cin >> c[i] >> w[i] >> p[i];
        int s;
        if (p[i] == 0) // 完全转化为多重
            s = V / c[i];
        else
            s = min(p[i], V / c[i]);
        for (int k = 1; s > 0; k <<= 1)
        {
            k = min(k, s);
            s -= k;
            for (int j = V; j >= k * c[i]; j--)
                dp[j] = max(dp[j], dp[j - k * c[i]] + k * w[i]);
        }
    }
    cout << dp[V] << endl;
}

二维费用背包问题

 定义：每件物品需要同时花费两种不同的代价

dp[i][j][k]：表示前i种物品付出两种代价分别最大为j和k时可获得的最大价值

状态转移方程：

dp[i][j][k]=max(dp[i-1][j][k],dp[i-1][j-c[i]][k-m[i]]+w[i])

01背包代码（完全背包、多重背包可以类比）

for(int i=1;i<=n;i++)
    for(int j=V;j>=c[i];j--)
        for(int k=M;k>=m[i];k--)
            dp[j][k]=max(dp[j][k],dp[j-c[i]][k-m[i]]+w[i]);

AcWing 二维费用的背包问题 

const int N = 1010; // 注意初始化，否则会越界
int c[N], w[N], m[N], dp[N][N];
inline void solve()
{
    int N, V, M;
    cin >> N >> V >> M;

    for (int i = 1; i <= N; i++)
    {
        cin >> c[i] >> m[i] >> w[i];
        for (int j = V; j >= c[i]; j--)
            for (int k = M; k >= m[i]; k--)
                dp[j][k] = max(dp[j][k], dp[j - c[i]][k - m[i]] + w[i]);
    }
    cout << dp[V][M] << endl;
}

Luogu P1507NASA的食物计划

const int N = 1010; // 注意初始化，否则会越界
int c[N], w[N], m[N], dp[N][N];
inline void solve()
{
    int V, M, N;
    cin >> V >> M >> N;

    for (int i = 1; i <= N; i++)
    {
        cin >> c[i] >> m[i] >> w[i];
        for (int j = V; j >= c[i]; j--)
            for (int k = M; k >= m[i]; k--)
                dp[j][k] = max(dp[j][k], dp[j - c[i]][k - m[i]] + w[i]);
    }
    cout << dp[V][M] << endl;
}

分组背包问题

  定义：

dp[k][j]：表示前k组物品花费代价j能取得的最大价值

子问题第k组物品状态：

①不选该组物品：dp[k][j]=dp[k-1][j];
②选该组物品：dp[k][j]=dp[k-1][j-c[i]+w[i]] 物品i属于k组

状态转移方程：

dp[k][j]=max(dp[k-1][j],dp[k-1][j-c[i]]+w[i])

模板：

 for (int k = 1; k <= N; k++)
    {
        int s;
        cin >> s; // 第k组的物品数量
        for (int i = 1; i <= s; i++)
            cin >> c[i] >> w[i]; // 组中每个物品i的属性
        for (int j = V; j >= 0; j--)
            for (int i = 1; i <= s; i++) // 保证每组物品只能选一个，可以覆盖之前组内物品最优解的来取最大值
                if (j >= c[i])
                    dp[j] = max(dp[j], dp[j - c[i]] + w[i]);
    }

AcWing 分组背包问题

const int N = 110; // 注意初始化，否则会越界
int c[N], w[N], m[N], dp[N];
inline void solve()
{
    int N, V;
    cin >> N >> V;
    for (int k = 1; k <= N; k++)
    {
        int s;
        cin >> s; // 第k组的物品数量
        for (int i = 1; i <= s; i++)
            cin >> c[i] >> w[i]; // 组中每个物品i的属性
        for (int j = V; j >= 0; j--)
            for (int i = 1; i <= s; i++) // 保证每组物品只能选一个，可以覆盖之前组内物品最优解的来取最大值
                if (j >= c[i])
                    dp[j] = max(dp[j], dp[j - c[i]] + w[i]);
    }
    cout << dp[V] << endl;
}

Luogu P1757 通天之分组背包

const int N = 110;  // 注意初始化，否则会越界
const int M = 1010; // 注意初始化，否则会越界
int c[M], w[M], dp[M];
int g[N][N], b[M]; // g[k][i]表示小组k种第i个物品的编号,b[k]表示小组k的物品+1；
inline void solve()
{
    int N, V;
    cin >> V >> N;
    int t = 0, k = 0;
    for (int i = 1; i <= N; i++)
    {
        cin >> c[i] >> w[i] >> k;
        t = max(t, k);  // 求小组的组数
        b[k]++;         // 小组k的物品+1；
        g[k][b[k]] = i; // 小组k中第b[k]个物品的编号为i;
    }
    for (int k = 1; k <= t; k++)
        for (int j = V; j >= 0; j--)
            for (int i = 1; i <= b[k]; i++)
                if (j >= c[g[k][i]])
                    dp[j] = max(dp[j], dp[j - c[g[k][i]]] + w[g[k][i]]);

    cout << dp[V] << endl;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1054407.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

JavaSE学习之--抽象类和接口

JavaSE学习之--抽象类和接口

&#x1f495;"没有眼泪我们就会迷路&#xff0c;彻底变成石头&#xff0c;我们的心会变成冰凌&#xff0c;吻会变成冰块。"&#x1f495; 作者&#xff1a;Mylvzi 文章主要内容&#xff1a;JavaSE学习之--抽象类和接口 一.抽象类 1.抽象类的定义 我们知道&#x…
阅读更多...
数仓精品理论-做大数据还有没有前途？

数仓精品理论-做大数据还有没有前途？

数仓精品理论-做大数据还有没有前途&#xff1f; 做大数据还有没有前途&#xff1f;大数据三要三不要我来讲讲大数据前景 做大数据还有没有前途&#xff1f; 先说&#xff0c;答案是肯定的&#xff0c;但一定要记住三要三不要。 datapulse官网&#xff1a; github:https://data…
阅读更多...
cesium gltf控制

cesium gltf控制

gltf格式详解 glTF格式本质上是一个JSON文件。这一文件描述了整个3D场景的内容。它包含了对场景结构进行描述的场景图。场景中的3D对象通过场景结点引用网格进行定义。材质定义了3D对象的外观，动画定义了3D对象的变换操作(比如选择、平移操作)。蒙皮定义了3D对象如何进行骨骼…
阅读更多...
黑豹程序员-架构师学习路线图-百科：HTML-网页三剑客

黑豹程序员-架构师学习路线图-百科：HTML-网页三剑客

为什么需要HTML 在网站技术发达之前&#xff0c;千年来我们获取信息是通过书籍。电脑流行后我们看文章、小说通过txt文件。看图通过单独的图片流量工具看单个的图片文件。 而HTML把文字和图片一起展示&#xff0c;让今天的电子书成为可能。 另外一点&#xff0c;我们的信息是…
阅读更多...
【操作系统】了解Linux操作系统中PCB进程管理模块与进程PID

【操作系统】了解Linux操作系统中PCB进程管理模块与进程PID

本篇要分享的内容是有关于操作系统中进程的内容。 目录 1.进程的简单理解 2.了解task_struct&#xff08;进程控制模块&#xff09;内容分类 3.task_struct&#xff08;进程控制模块&#xff09;中的PID 4.调用查看PID的函数 1.进程的简单理解 首先我们需要理解的是什么是…
阅读更多...
简单讲解 glm::mat4

简单讲解 glm::mat4

文章目录 前言一、下载glm库二、基本数学知识1. 三维中的 4 x 4 矩阵2.旋转3. 位移4. 缩放5. 组合 三、行向量或列向量四、总结 前言 glm库是OpenGL的官方数学库&#xff0c;里面内置多种跟几何变换相关的函数&#xff0c;熟练掌握glm库可以省下很多麻烦。 因为最近在项目中主…
阅读更多...
鞋类 整鞋试验方法 剥离强度

鞋类 整鞋试验方法 剥离强度

声明 本文是学习GB-T 3903.3-2011 鞋类 整鞋试验方法 剥离强度. 而整理的学习笔记,分享出来希望更多人受益,如果存在侵权请及时联系我们 1 范围 GB/T 3903 的本部分规定了整鞋鞋底与鞋帮或外底与外中底之间剥离强度的试验方法。 本部分适用于采用模压、硫化、注塑、灌注、胶…
阅读更多...
暴力破解及验证码安全

暴力破解及验证码安全

1.暴力破解注意事项 1、破解前一定要有一个有郊的字典&#xff08;Top100 TOP2000 csdn QQ 163等密码&#xff09; https://www.bugku.com/mima/ 密码生成器 2、判断用户是否设置了复杂的密码 在注册页面注册一个,用简单密码看是否可以注册成功 3、网站是…
阅读更多...
Jenkins集成AppScan实现

Jenkins集成AppScan实现

一、Jenkins上安装插件 在Jenkins里安装以下插件 ibm-security-appscanstandard-scanner 二、打开AppScan 1、配置需要扫描的地址 配置需要扫描的地址 2、记录好要扫描的URL登录序列 记录好要扫描的URL登录序列 3、导出要扫描的URL登录序列设置 导出要扫描的URL登录序列设置 三…
阅读更多...
C程序设计内容与例题讲解 -- 第四章--选择结构程序设计(第五版)谭浩强

C程序设计内容与例题讲解 -- 第四章--选择结构程序设计(第五版)谭浩强

前言&#xff1a;在第三章我们介绍了顺序结构程序设计。在顺序结构中&#xff0c;各个语句是按自上而下的顺序执行的&#xff0c;执行完上一个语句就自动执行下一个语句&#xff0c;是无条件的&#xff0c;不必做任何判断。是这最简单的程序结构。实际上&#xff0c;在很多情况…
阅读更多...
IDEA 配置 Maven（解决依赖下载缓慢）

IDEA 配置 Maven（解决依赖下载缓慢）

IDEA 配置 Maven&#xff08;解决依赖下载缓慢&#xff09; 这一篇主要介绍 Maven 的基本用法。等我之后学习到框架知识时&#xff0c;会完善此部分内容。 一、Maven 简介 Maven 是专门用于管理和构建 Java 项目的工具&#xff0c;Apache Maven 是一个项目管理和构建工具&#…
阅读更多...
ali内核服务器搭建Linux版本的小皮面板(微调)

ali内核服务器搭建Linux版本的小皮面板(微调)

一、搭建小皮面板 windows版本的小皮面板我们经常使用,早就熟悉了搭建和配置 那么这里我们就来使用Linux版本的小皮面板,看看如何进行操作 安装网址: https://www.xp.cn/linux.html 这里根据自己的操作系统选择合适的命令 我使用的是kali搭建,因此选择Debian安装脚本 注意:…
阅读更多...
28270-2012 智能型阀门电动装置 学习笔记

28270-2012 智能型阀门电动装置 学习笔记

声明 本文是学习GB-T 28270-2012 智能型阀门电动装置. 而整理的学习笔记,分享出来希望更多人受益,如果存在侵权请及时联系我们 1 范围 本标准规定了智能型阀门电动装置(以下简称智能电装)的术语、技术要求、试验方法、检验规则、标 志、包装、运输和贮存条件等。 本标准适…
阅读更多...
24Hibench

24Hibench

1. Hibench 官网 ​ HiBench is a big data benchmark suite that helps evaluate different big data frameworks in terms of speed, throughput and system resource utilizations. It contains a set of Hadoop, Spark and streaming workloads, including Sort, WordCou…
阅读更多...
国庆放假作业2

国庆放假作业2

1、select实现服务器并发 #include <myhead.h>#define PORT 7373 #define IP "192.168.1.9"int main(int argc,const char *argv[]) {//创建报式套接字int sfdsocket(AF_INET,SOCK_STREAM,0);if(sfd<0){ERR_MSG("socket error");return -1;}prin…
阅读更多...
MATLAB与Python：优势与挑战

MATLAB与Python：优势与挑战

本文旨在探讨MATLAB与Python在特定领域内的使用情况&#xff0c;并分析两者之间的优势和挑战。 MATLAB和Python都是流行的编程语言&#xff0c;广泛应用于科学计算、数据分析和机器学习等领域。在某些领域&#xff0c;如航空航天工程、自动化和电子工程嵌入式系统开发等&#…
阅读更多...
【分布式事务】

【分布式事务】

文章目录 解决分布式事务的思路seata四种模式1. XA模式2. AT模式AT模式与XA模式的区别是什么&#xff1f;脏写问题 3. TCC模式事务悬挂和空回滚 4. SAGA模式 四种模式对比口述AT模式与TCC模式高可用 什么是分布式事务&#xff1f; 分布式事务&#xff0c;就是指不是在单个服务或…
阅读更多...
Arduino ESP32/ESP8266 +ST7735 1.8“tft中秋小时钟

Arduino ESP32/ESP8266 +ST7735 1.8“tft中秋小时钟

Arduino ESP32 ST7735 1.8"tft中秋小时钟 &#x1f33c;原作者B站视频&#xff1a; ESP32中秋小时钟&#xff0c;表盘自动切换&#xff0c;代码开源&#xff0c;原图可下载&#xff08;案例应用&#xff09; &#x1f39e;tft ST7735 128160 1.8" 显示效果:(由于原作…
阅读更多...
【vue3】wacth监听，监听ref定义的数据，监听reactive定义的数据，详解踩坑点

【vue3】wacth监听，监听ref定义的数据，监听reactive定义的数据，详解踩坑点

假期第二篇&#xff0c;对于基础的知识点&#xff0c;我感觉自己还是很薄弱的。 趁着假期&#xff0c;再去复习一遍 之前已经记录了一篇【vue3基础知识点-computed和watch】 今天在学习的过程中发现&#xff0c;之前记录的这一篇果然是很基础的&#xff0c;很多东西都讲的不够…
阅读更多...
gcc中-I（大写的i）参数的作用

gcc中-I（大写的i）参数的作用

《gcc -I -L -l区别》是我参考的一篇博客。 gcc中-I参数可以帮助找到头文件的目录&#xff0c;比如在当前目录下有一个名为includeTestCom.c的c文件和名为includeCom的目录。 includeTestCom.c里边的内容如下&#xff1a; #include "good.h" int main(){printf(&q…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023