概述
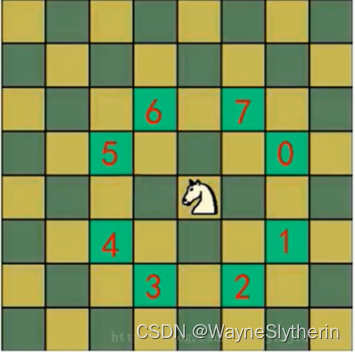
骑士周游算法,叫做“马踏棋盘算法”或许更加直观。在国际象棋8x8的棋盘中,马也是走“日字”进行移动,相应的产生了一个问题:“如果要求马 在每个方格只能进入一次,走遍全部的64个方格需要如何行进?”这就是著名的 骑士周游算法的由来。
思路
相信大家看到这个问题首先想到就是回溯。
马踏棋盘问题(骑士周游问题) 实际上是图的深度优先搜索(DFS)的应用。
如果使用回溯(就是深度优先搜索) 来解决,假如马儿踏了53个点,走到了第53个,坐标(1,0),发现已经走到尽头,没办法,那就只能回退了,查看其他的路径,就在棋盘上不停的回溯。
基于回溯的解决方案
- 创建棋盘chessBoard,是一个二维数组;
- 将当前位置设置为已经访问,然后根据当前位置,计算马还能走哪些位置,并放入到一个集合中(ArrayList),最多有8个位置,每走一步,就使用step+1;
- 遍历arrayList中存放的所有位置,看看哪个可以走通;
- 判断马儿是否完成了任务,使用step和应该走的步数(即棋盘格子数-1)比较,如果没有达到数量,则表示没有完成任务,将整个棋盘置0;
注:马 不同的走法(策略),会得到不同的结果,效率也会有影响(优化)。
代码实现
public class HorseChessBoard {
private static int X;//棋盘的列数
private static int Y;//棋盘的行数
//创建一个数组, 标记棋盘的各个位置是否被访问过
private static boolean visited[];
//试用一个属性,标记是否棋盘的所有位置都被访问过了
private static boolean finished;//如果为true,表示成功
public static void main(String[] args) {
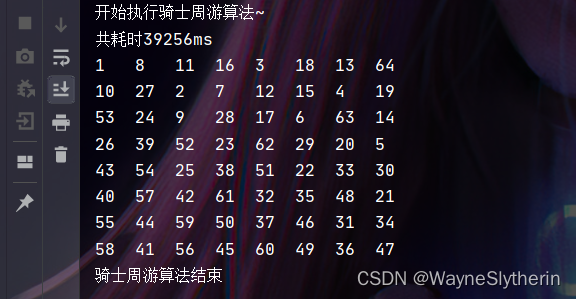
System.out.println("开始执行骑士周游算法~");
//测试
X = 8;
Y = 8;
int row = 1;//马儿初始位置的行,从1开始编号
int column = 1;//马儿初始位置的列,从1开始编号
//创建棋盘
int[][] chessboard = new int[X][Y];
visited = new boolean[X*Y];//初始值都是false
//测试一下耗时
long start = System.currentTimeMillis();
traversalCheessBoard(chessboard,row-1,column-1,1);
long end = System.currentTimeMillis();
System.out.println("共耗时"+(end - start)+"ms");
//输出棋盘的最终状况
for (int[] rows : chessboard) {
for (int step : rows) {
System.out.print(step+"\t");
}
System.out.println();
}
System.out.println("骑士周游算法结束");
}
/**
* 骑士周游问题算法
* @param chessBoard 棋盘
* @param row 马儿当前位置的行 从0开始
* @param column 马儿当前位置的列 从0开始
* @param step 是第几步,初始位置是第1步
*/
public static void traversalCheessBoard(int[][] chessBoard,int row,int column,int step){
chessBoard[row][column] = step;
//row = 4; X=8; column=4; 4*8+4=36;
visited[row*X+column] = true;//标记该位置已经访问
//获取当前位置可以走的下一个位置的集合
ArrayList<Point> ps = next(new Point(column, row));
//遍历ps
while (!ps.isEmpty()){
Point p = ps.remove(0);//取出下一个可以走的位置
//判断该点是否已经访问过
if(!visited[p.y*X+p.x]){//说明还没访问过
traversalCheessBoard(chessBoard,p.y,p.x,step+1);
}
}
//判断马儿是否完成了任务,使用step和应该走的步数(即棋盘格子数-1)比较,
//如果没有达到数量,则表示没有完成任务,将整个棋盘置0;
//说明: step<X*Y成立的情况有两种
//1.棋盘到目前位置,仍然没有走完
//2.棋盘处于回溯过程
if (step<X*Y&&!finished){
chessBoard[row][column]=0;
visited[row * X + column] = false;
}else {
finished = true;
}
}
/**
* 根据当前位置(Point) ,计算马儿还能走哪些位置(Point),并放入到一个集合中(ArrayList),最多有八个位置
* @param curPoint
* @return
*/
public static ArrayList<Point> next(Point curPoint){
//创建一个ArrayList
ArrayList<Point> ps = new ArrayList<>();
//创建一个Point
Point p1 = new Point();
//判断马儿下一步是否可以走,若可以,将这个位置放入集合
//判断马儿是否可以走 位置5
if ((p1.x=curPoint.x-2)>=0 && (p1.y = curPoint.y-1)>=0){
ps.add(new Point(p1));
}
//判断马儿是否可以走 位置6
if ((p1.x=curPoint.x-1)>=0 && (p1.y = curPoint.y-2)>=0){
ps.add(new Point(p1));
}
//判断马儿是否可以走 位置7
if ((p1.x=curPoint.x+1) < X && (p1.y = curPoint.y-2)>=0){
ps.add(new Point(p1));
}
//判断马儿是否可以走 位置0
if ((p1.x=curPoint.x+2) < X && (p1.y = curPoint.y-1)>=0){
ps.add(new Point(p1));
}
//判断马儿是否可以走 位置1
if ((p1.x=curPoint.x+2) < X && (p1.y = curPoint.y+1)< Y){
ps.add(new Point(p1));
}
//判断马儿是否可以走 位置2
if ((p1.x=curPoint.x+1)<X && (p1.y = curPoint.y+2)<Y){
ps.add(new Point(p1));
}
//判断马儿是否可以走 位置3
if ((p1.x=curPoint.x-1)>=0 && (p1.y = curPoint.y+2)<Y){
ps.add(new Point(p1));
}
//判断马儿是否可以走 位置4
if ((p1.x=curPoint.x-2)>=0 && (p1.y = curPoint.y+1)<Y){
ps.add(new Point(p1));
}
return ps;
}
}
效率分析
采用回溯的方案思路上自然是可行的,那么它的效率究竟如何呢?可以说很不乐观!测算下来差不多要40秒左右,优化的空间很大。
回溯分析与贪心优化
我们思考可以在此思考一下上面解决方案的是否有可以优化的地方?能否用贪心算法进行优化呢?
- 我们获取当前位置,可以走的下一个位置的集合:
ArrayList ps = next(new Point(column,row)); - 需要对ps中所有Point 下一步的所有集合数目进行非递减排序;
a. 递减是:9,7,6,5,4…
b. 递增排序:4,5,6,7,8…
c. 非递减排序: 1,2,2,3,3,4,4,4,4,4,4,4,5,8,10…
d. 非递增排序: 9,9,9,8,7,5,3… - 如果下一步的选择越少,意味着回溯时的步骤越少,相应的效率也会越高,所以我们应该采用非递减排序,使得回溯的代价尽可能的低。
核心优化代码
我们不妨编写一个方法,根据当前这一步的所有下一步的选择位置,进行非递减排序,以求减少回溯的次数
public static void sort(ArrayList<Point> ps){
ps.sort(new Comparator<Point>(){
@Override
public int compare(Point o1, Point o2) {
//获取到o1的下一步的所有位置个数
int count1 = next(o1).size();
//获取到o2的下一步的所有位置个数
int count2 = next(o2).size();
if (count1<count2){
return -1;
}else if (count1==count2){
return 0;
}else {
return 1;
}
}
});
}
这样,在上面的回溯算法中,我们可以先对ps进行排序处理,再进行后面的测算
//获取当前位置可以走的下一个位置的集合
ArrayList<Point> ps = next(new Point(column, row));
//对ps进行排序,排序的规则就是对ps的所有的Point对象的下一步的位置数目进行非递减排序
sort(ps);
//遍历ps
while (!ps.isEmpty()){
Point p = ps.remove(0);//取出下一个可以走的位置
//判断该点是否已经访问过
if(!visited[p.y*X+p.x]){//说明还没访问过
traversalCheessBoard(chessBoard,p.y,p.x,step+1);
}
}
效率分析
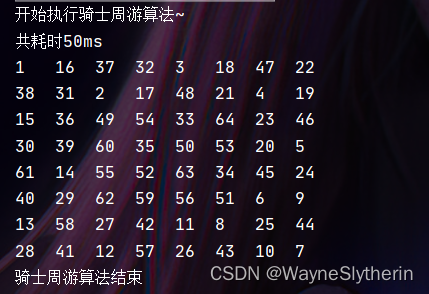
经过贪心算法的优化后,相同的配置下,测算时间直接降到了50ms,效率比之前提升600倍。还是很可观的提升的。
小结
本节,先是采用回溯算法对骑士周游问题进行了拆解,而后利用贪心算法对回溯算法进行了优化解决了骑士周游问题。相信借此我们对贪心算法的应用应该都有了更深层次的理解,算法千万条,应用第一条,只有在合适的场景才能发挥出其最大的作用。
关注我,共同进步,每周至少一更。——Wayne