目录
前言
1.什么是二叉排序树
2.如何构建二叉排序树
3.二叉排序树的操作
3.1定义节点储存方式
3.2插入节点操作
3.2创建二叉排序树
3.4遍历输出(中序遍历)
3.5数据查找操作
3.6获取最大值和最小值
3.7删除节点操作
3.8销毁二叉排序树
4.完整代码
前言
今天我们继续学习新的知识点----排序二叉树,在此之前我们学习了相关的排序算法,给你一个数组,然后对这个数组进行排序。那么同样的我们也可以去构建一个二叉排序树,在创建树的过程中进行排序,也能实现排序的效果,下面就一起来看看吧!
1.什么是二叉排序树
二叉排序树(Binary Sort Tree),又称二叉查找树(Binary Search Tree),亦称二叉搜索树。是数据结构中的一类。在一般情况下,查询效率比链表结构要高。
给定一个二叉树,如果满足以下条件,那就是二叉排序树
- 若它的左子树不空,则左子树上所有结点的值均小于它根结点的值。
- 若它的右子树不空,则右子树上所有结点的值均大于它根结点的值。
- 它的左、右子树都满足为⼆叉排序树
二叉排序树最大的好处就是查找效率高,相较于链表一个一个去查找,二叉排序树可以去根据数据的排序规律来进行查找
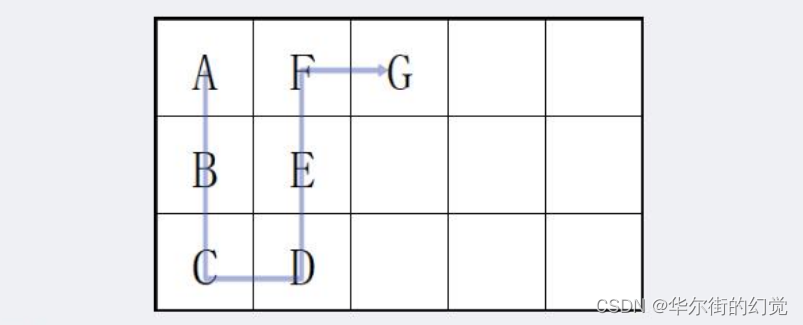
二叉排序树图示: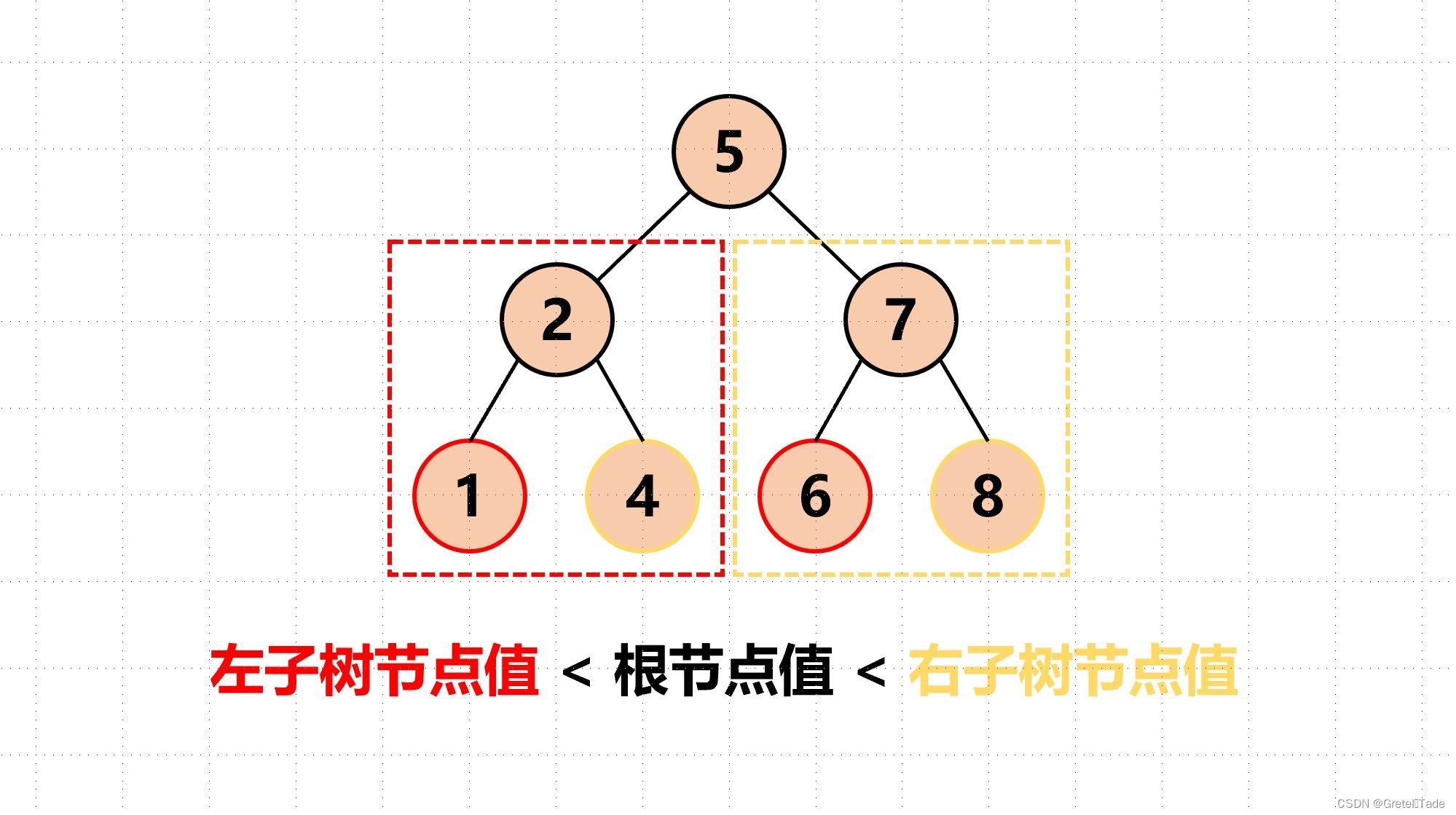
2.如何构建二叉排序树
比如给定一个数组 [62,88,58,47,35,73,51,99,37,93] ,首先拿到第一个数字,以这个数字为根结点(标准),进行构建,如果比这个数字要大的就放到右子树,比这个要小的就放到左子树去,如下图所示:

这里我们可以看出,这些节点是一个一个去进行插入的,那我们就可以去通过递归插入的方式来创建,依次往下遍历,找到合适的位置再进行插入操作。
3.二叉排序树的操作
3.1定义节点储存方式
#include<stdio.h>
#include<stdlib.h>
//二叉排序树节点存储方式
typedef int DataType;
typedef struct binarytreenode {
DataType data; //数据域
struct binarytreenode* left; //左指针
struct binarytreenode* right; //右指针
}BTnode;3.2插入节点操作
插入一个节点首先就要找到这个节点应该插入的位置,从跟节点开始,如果比跟节点小就往左,大就往右,直到叶子节点的位置进行插入操作。

代码实现:
//插入数据
void Insert_node(BTnode** root, DataType data) {
if (*root == NULL) {
*root = (BTnode*)malloc(sizeof(BTnode));
if (!*root) {
printf("ERROR\n");
exit(-1);
}
(*root)->data = data;
(*root)->left = NULL;
(*root)->right = NULL;
}
else if ((*root)->data <= data)
Insert_node(&(*root)->right, data);
else if ((*root)->data > data)
Insert_node(&(*root)->left, data);
}3.2创建二叉排序树
创建二叉排序树,只需要一一插入节点,最后返回根节点即可。代码如下:
//创建排序二叉树
BTnode* Create_sortBtree(DataType* arr, int size) {
if (!arr)
return NULL;
else {
BTnode* T = NULL;
for (int i = 0; i < size; i++) {
Insert_node(&T, arr[i]);
}
return T;
}
}3.4遍历输出(中序遍历)
//中序遍历排序二叉树
void mid_travel(BTnode* T)
{
if (!T)
return;
mid_travel(T->left);
printf("%d ", T->data);
mid_travel(T->right);
}3.5数据查找操作
在二叉排序树上查找某一个值节点,然后返回这个节点的操作。这里可以通过递归和非递归两种方法去实现,代码如下:
递归实现:
BTnode* Btree_search(BTnode* root, DataType target) {
if (!root)
return NULL;
if (target == root->data) {
return root;
}
return target > root->data ? Btree_search(root->right, target) : Btree_search(root->left, target);
}非递归实现(迭代实现):
//非递归查找
BTnode* Btree_search_fa(BTnode* T, DataType target) {
BTnode* p = T;
while (p) {
if (p->data == target)
{
return p;
}
p = target > p->data ? p->right : p->left;
}
return NULL;
}3.6获取最大值和最小值
在一个排序二叉树里面获取最大值或者是最小值,说白了也就是找到最右边和最左边节点就行了,二叉排序树的两个最值就在最两边。代码如下:
获取最大值
//获取最大值
int Btree_max(BTnode* T) {
BTnode* cur = T;
while (cur->right) {
cur = cur->right;
}
return cur->data;
}获取最小值
//获取最小值
int Btree_min(BTnode* T) {
BTnode* cur = T;
while (cur->left) {
cur = cur->left;
}
return cur->data;
}
3.7删除节点操作
删除节点操作,这就有可能会破坏到排序二叉树的结构,所以要分几种情况去处理。一、如果删除的是叶子节点的话,那么就可以直接去删除,因为叶子节点左右节点都为空,不会影响到二叉排序树的结构;二、如果要删除的节点只有一个左子树或者是有一个右子树的话,我们只需要找到这个节点的左节点或者是右节点,然后顶替掉这个要删除的节点即可;三、如果要删除的节点都有左右子树的话,这里我们就需要去遍历找到比这个节点大一位或者是小一位的节点来顶替这个节点。如下图所示:
1.删除叶子节点
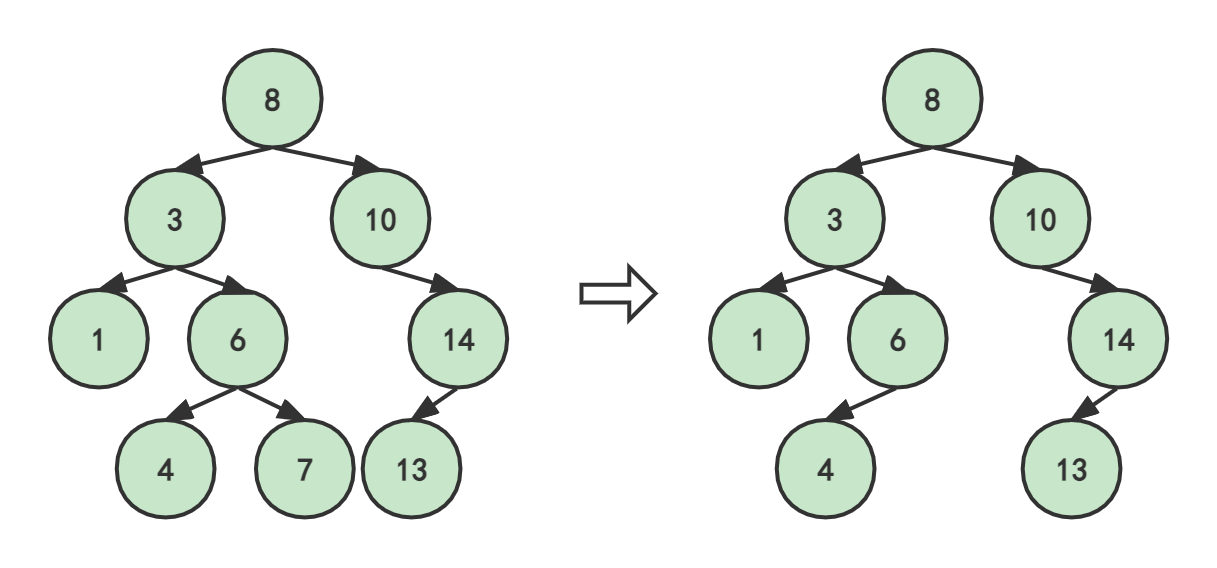
2.删除只有一个左(右)子树的节点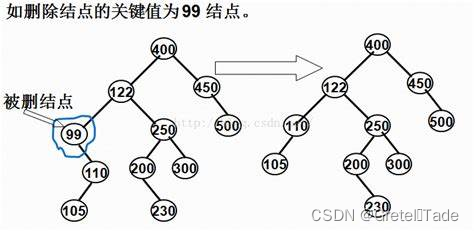
3.删除有左右子树的节点
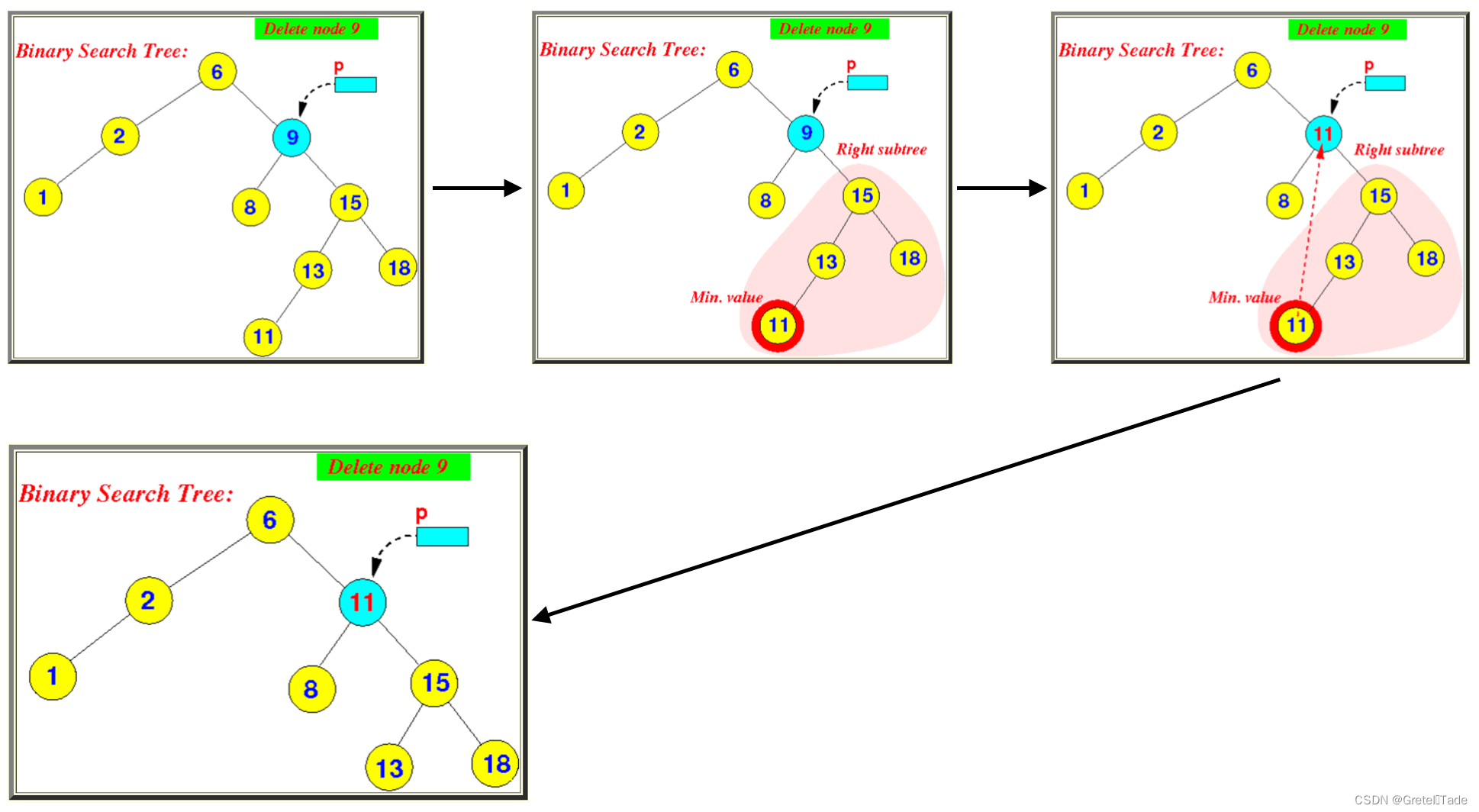

代码实现:
//删除节点
void Btree_del(BTnode* T, DataType l) {
if (!T) {
printf("fuck no\n");
return;
}
//找到这个要删除节点的父节点
BTnode* p = T, * f = NULL;
while (p) {
if (p->data == l)
{
break;
}
f = p;
p = l > p->data ? p->right : p->left;
}
if (!p)
{
printf("没有这个节点\n");
return;
}
BTnode* target = p;//此时的要删除目标节点
BTnode* par = f; //此时要删除节点的父节点
//第一种情况 此节点只有一个子树的时候
if (!target->left && target->right != NULL)
{
if (target->data > par->data) {
par->right = target->right;
}
else {
par->left = target->right;
}
free(target);//释放空间
target = NULL;
}
else if (target->left != NULL && !target->right) {
if (target->data > par->data) {
par->right = target->left;
}
else {
par->left = target->left;
}
free(target);
target = NULL;
}
//第二种情况,如果删除的是叶节点,直接删除即可
else if (!target->left && !target->right) {
if (target->data > par->data) {
par->right = NULL;
}
else {
par->left = NULL;
}
free(target);
target = NULL;
}
//第三种情况,如果左右子树都存在的话
//可以用右子树的最小元素
//或者左子树的最大元素来替代被删除的节点
//我这里就直接去用左树的最大代替这个节点
else
{
BTnode* Lchild = target->left;
while (Lchild->right != NULL) {
Lchild = Lchild->right;
}
if (target->data > par->data) {
par->right = Lchild;
}
else {
par->left = Lchild;
}
free(target);
target = NULL;
}
printf("Deleting successfully\n");
}3.8销毁二叉排序树
//销毁
void Destory_btree(BTnode* T) {
if (!T)
return;
BTnode* cur = T;
if (cur->left)
Destory_btree(cur->left);
if (cur->right)
Destory_btree(cur->right);
free(T);
}4.完整代码
#include<stdio.h>
#include<stdlib.h>
//二叉排序树节点存储方式
typedef int DataType;
typedef struct binarytreenode {
DataType data; //数据域
struct binarytreenode* left; //左指针
struct binarytreenode* right; //右指针
}BTnode;
//插入数据
void Insert_node(BTnode** root, DataType data) {
if (*root == NULL) {
*root = (BTnode*)malloc(sizeof(BTnode));
if (!*root) {
printf("ERROR\n");
exit(-1);
}
(*root)->data = data;
(*root)->left = NULL;
(*root)->right = NULL;
}
else if ((*root)->data <= data)
Insert_node(&(*root)->right, data);
else if ((*root)->data > data)
Insert_node(&(*root)->left, data);
}
//创建排序二叉树
BTnode* Create_sortBtree(DataType* arr, int size) {
if (!arr)
return NULL;
else {
BTnode* T = NULL;
for (int i = 0; i < size; i++) {
Insert_node(&T, arr[i]);
}
return T;
}
}
//中序遍历排序二叉树
void mid_travel(BTnode* T)
{
if (!T)
return;
mid_travel(T->left);
printf("%d ", T->data);
mid_travel(T->right);
}
//递归查找数据
BTnode* Btree_search(BTnode* root, DataType target) {
if (!root)
return NULL;
if (target == root->data) {
return root;
}
return target > root->data ? Btree_search(root->right, target) : Btree_search(root->left, target);
}
//非递归查找
BTnode* Btree_search_fa(BTnode* T, DataType target) {
BTnode* p = T, * f = NULL;
while (p) {
if (p->data == target)
{
return f;
}
f = p;
p = target > p->data ? p->right : p->left;
}
return NULL;
}
//获取最大值
int Btree_max(BTnode* T) {
BTnode* cur = T;
while (cur->right) {
cur = cur->right;
}
return cur->data;
}
//获取最小值
int Btree_min(BTnode* T) {
BTnode* cur = T;
while (cur->left) {
cur = cur->left;
}
return cur->data;
}
//删除节点
void Btree_del(BTnode* T, DataType l) {
if (!T) {
printf("fuck no\n");
return;
}
//找到这个要删除节点的父节点
BTnode* p = T, * f = NULL;
while (p) {
if (p->data == l)
{
break;
}
f = p;
p = l > p->data ? p->right : p->left;
}
if (!p)
{
printf("没有这个节点\n");
return;
}
BTnode* target = p;//此时的要删除目标节点
BTnode* par = f; //此时要删除节点的父节点
//第一种情况 此节点只有一个子树的时候
if (!target->left && target->right != NULL)
{
if (target->data > par->data) {
par->right = target->right;
}
else {
par->left = target->right;
}
free(target);//释放空间
target = NULL;
}
else if (target->left != NULL && !target->right) {
if (target->data > par->data) {
par->right = target->left;
}
else {
par->left = target->left;
}
free(target);
target = NULL;
}
//第二种情况,如果删除的是叶节点,直接删除即可
else if (!target->left && !target->right) {
if (target->data > par->data) {
par->right = NULL;
}
else {
par->left = NULL;
}
free(target);
target = NULL;
}
//第三种情况,如果左右子树都存在的话
//可以用右子树的最小元素
//或者左子树的最大元素来替代被删除的节点
//我这里就直接去用左树的最大代替这个节点
else
{
BTnode* Lchild = target->left;
while (Lchild->right != NULL) {
Lchild = Lchild->right;
}
if (target->data > par->data) {
par->right = Lchild;
}
else {
par->left = Lchild;
}
free(target);
target = NULL;
}
printf("Deleting successfully\n");
}
//销毁
void Destory_btree(BTnode* T) {
if (!T)
return;
BTnode* cur = T;
if (cur->left)
Destory_btree(cur->left);
if (cur->right)
Destory_btree(cur->right);
free(T);
}
int main()
{
int a[] = { 53,17,78,9,45,65,87,23 };
//创建二叉排序树
BTnode* T = Create_sortBtree(a, sizeof(a) / sizeof(int));
mid_travel(T);//遍历输出
puts("");
//删除最大最小值
printf("max:%d min:%d\n", Btree_max(T), Btree_min(T));
//查找
BTnode* find = Btree_search(T, 23);
printf("查找结果%d\n", find->data);
//删除节点
Btree_del(T, 45);
mid_travel(T);
puts("");
//销毁操作
Destory_btree(T);
}
//输出结果:
//9 17 23 45 53 65 78 87
//max:87 min : 9
//查找结果23
//Deleting successfully
//9 17 23 53 65 78 87
以上就是二叉排序树的全部内容了,我们下次见咯!祝各位国庆节快乐!