视频来源：b站直播
+周志华老师机器学习西瓜树+南瓜书
以下是我的学习笔记：

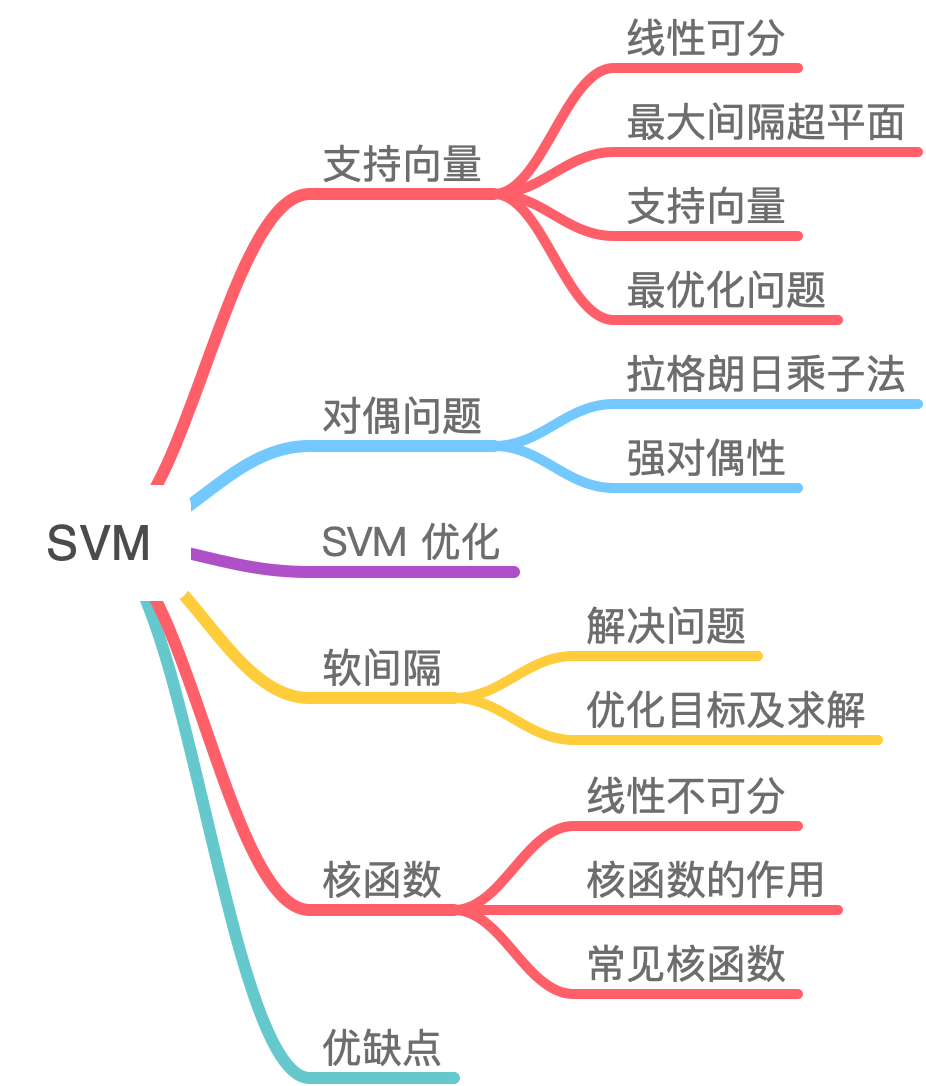
支持向量机（support vector machines，SVM）是一种二分类模型，它的目的是寻找一个超平面来对样本进行分割，分割的原则是间隔最大化，通过对偶问题，最终转化为一个凸二次规划问题来求解。由简至繁的模型包括：

• 当训练样本线性可分时，通过硬间隔最大化，学习一个线性可分支持向量机
• 当训练样本近似线性可分时，通过软间隔最大化，学习一个线性支持向量机
• 当训练样本线性不可分时，通过核技巧和软间隔最大化，学习一个非线性支持向量机

算法原理：从几何角度，对于线性可分数据集，支持向量机就是找距离正负样本都最远的超平面，相比于感知机，其解是唯一的，且不偏不倚，泛化性能更好。

三个重点“间隔（margin）” “对偶(duality)” “核技巧(kernel trick)”
以下是第一个证明：

最大间隔超平面

超平面是分割输入变量空间的线。
从二维扩展到多维空间中时，将和完全正确地划分开的就成了一个超平面。为了使这个超平面更具鲁棒性，我们会去找最佳超平面，以最大间隔把两类样本分开的超平面，也称之为最大间隔超平面。

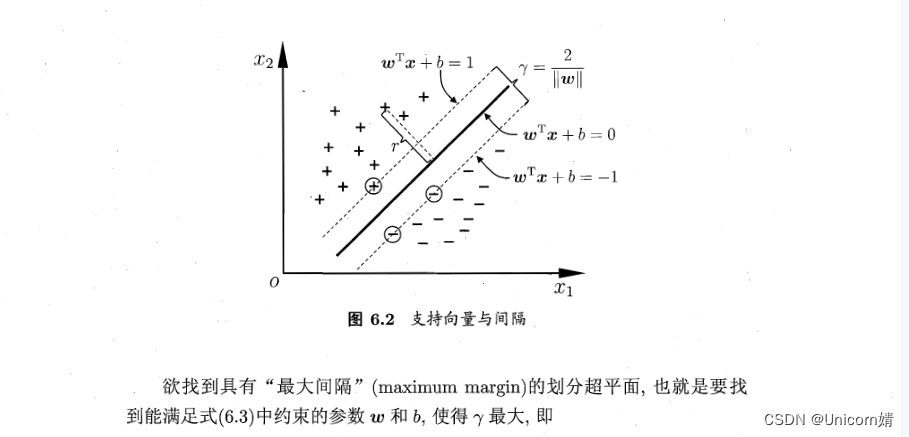
• 两类样本分别分割在该超平面的两侧；
• 两侧距离超平面最近的样本点到超平面的距离被最大化了

边距是最近类点上两条线之间的间隙。这被计算为从线到支持向量或最近点的垂直距离。如果类之间的边距较大，则认为是好的边距，较小的边距是差的边距。

处理非线性和不可分的平面

有些问题不能使用线性超平面解决，在这种情况下，SVM 使用内核技巧将输入空间转换为更高维空间，数据点绘制在 x 轴和 z 轴上（Z 是 x 和 y 的平方和：z=x^2=y2）。现在，您可以使用线性分离轻松分离这些点。

 显然，支持向量机（SVM）的目标函数是关于\boldsymbol{w}的凸函数，
  （海塞矩阵是半正定的）且其约束函数仍然为一个凸函数，
  因此支持向量机是一个凸优化问题。

我们现在面对的是不等式优化问题，针对这种情况其主要思想是将不等式约束条件转变为等式约束条件，引入松弛变量，将松弛变量也是为优化变量。

为什么支持向量机通常都采用拉格朗日对偶求解呢？
1.无论主问题是何种优化问题，对偶问题恒为凸优化问题，因此更容易求解（尽管支持向量机的主问题本就是凸优化问题），而且原始问题的时间复杂度和特征维数呈正比（因为未知量是w），而对偶问题和数据量成正比（因为未知量是），当特征维数远高于数据量的时候拉格朗日对偶更高效；
2.对偶问题能很自然地引入核函数，进而推广到非线性分类问题（最主要的原因）

核函数

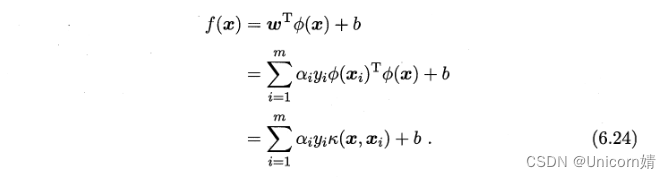
这里的函数K（.,.）就是核函数。只要一个对称矩阵所对应的核矩阵半正定，他就能作为一个核函数使用。
常用核函数：

强对偶性

非线性支持向量机

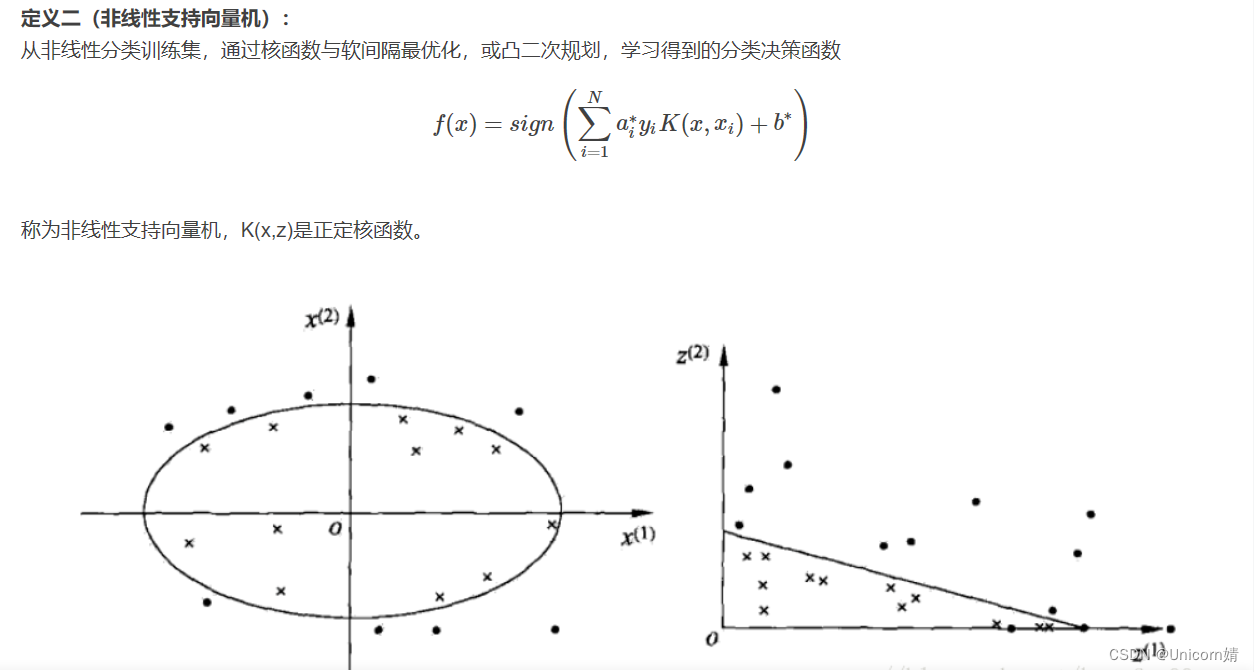
软间隔

算法原理：在现实任务中，线性不可分的情形才是最常见的，因此需要允许支持向量机犯错。
我们一直假定训练样本在样本空间或特征空间中是“线性可分”的，即存在一个超平面能将不同类样本完全划分开，这称为“硬间隔”。然而，在现实任务中，往往很难确定合适的核函数使得训练样本在特征空间中线性可分。即便恰好找到了某个核函数使训练集在特征空间中线性可分，也很难断定这个貌似线性可分的结果不是由于“过拟合”所造成的。为此，我们引入“软间隔”的概念，允许支持向量机在一些样本上出错。

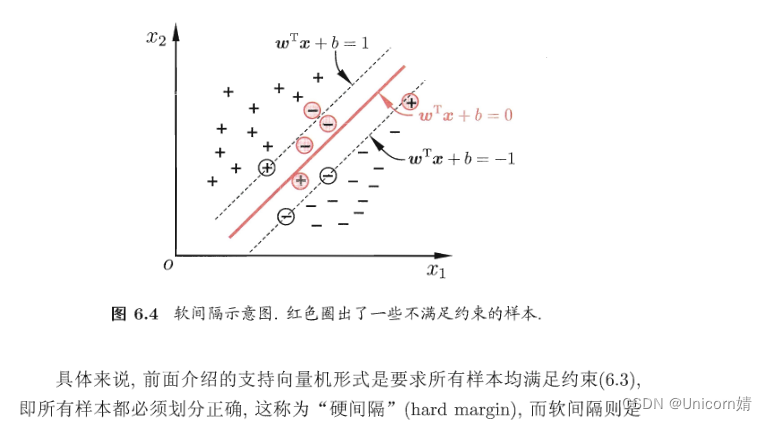
从数学角度来说，软间隔就是允许部分样本（但要尽可能少）不满足下式中的约束条件

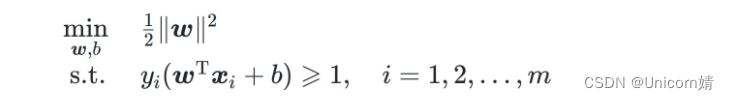
因此，可以将必须严格执行的约束条件转化为具有一定灵活性的“损失”，合格的损失函数要求如下：

• 当满足约束条件时，损失为0；
• 当不满足约束条件时，损失不为0，
• （可选）当不满足约束条件时，损失与其违反约束条件的程度成正比
  只有满足以上要求，才能保证在最小化（min）损失的过程中，保证不满足约束条件的,样本尽可能的少。
  
  其中，L0/1是“0/1损失函数”
  
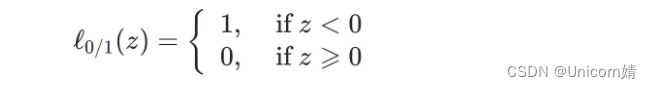
  C>0是一个常数，用来调节损失的权重，显然当C趋于无穷时，会迫使所有样本的损失为0，进而退化为严格执行的约束条件，退化为硬间隔，因此，本式子可以看作支持向量机的一般化形式。

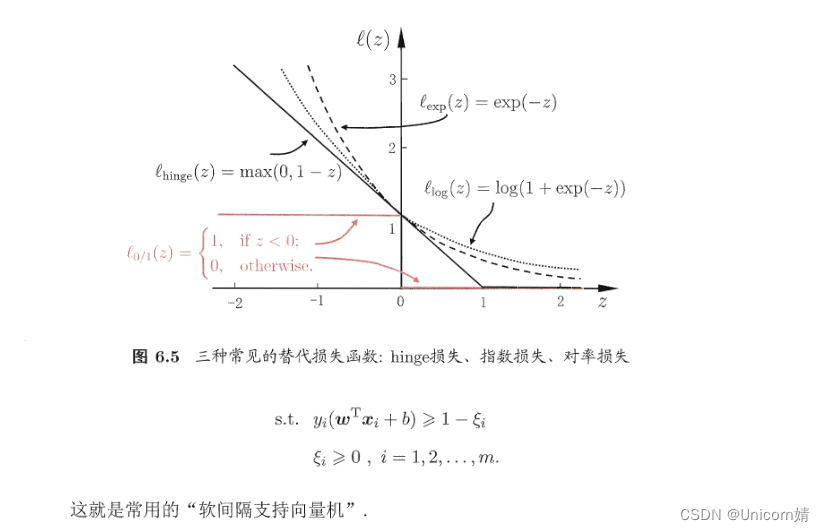
落在带子上的样本不计算损失（类比线性回归在线上的点预测误差为0），不在带子上的则以偏离带子的距离作为损失（类比线性回归的均方误差），然后以最小化损失的方式迫使间隔带从样本最密集的地方
（中心地带）穿过，进而达到拟合训练样本的目的。

优缺点

1、优点
与朴素贝叶斯算法相比，SVM 分类器提供了良好的准确性并执行更快的预测。它们还使用较少的内存，因为它在决策阶段使用训练点的子集。支持向量机在具有明显分离边距和高维空间的情况下效果很好。
具体如下：

• 可以解决高维问题，即大型特征空间；

• 解决小样本下机器学习问题；

• 能够处理非线性特征的相互作用；

• 无局部极小值问题；（相对于神经网络等算法）

• 无需依赖整个数据；

• 泛化能力比较强。
  2、缺点
  支持向量机不适合大型数据集，因为它的训练时间长，而且与朴素贝叶斯相比，它也需要更多的训练时
  间。它在重叠类中效果不佳，并且对使用的内核类型也很敏感。
  具体如下：

• 当观测样本很多时，效率并不是很高；

• 对非线性问题没有通用解决方案，有时候很难找到一个合适的核函数；

• 对于核函数的高维映射解释力不强，尤其是径向基函数；

• 常规SVM只支持二分类；

• 对缺失数据敏感。