【问题描述】
给定一个只有一个源点和一个汇点的有向图，要求求出所有的关键活动，并计算完成该工程至少需要多少时间。

【输入格式】
第一行包含两个整数 n 和 m，表示顶点数和边数。
接下来 m 行，每行包含三个整数 u，v，w，表示点 u 和点 v 之间存在一条权值为 w 的边。

【输出格式】
输出完成该工程至少需要多少时间及各条关键路径。
 

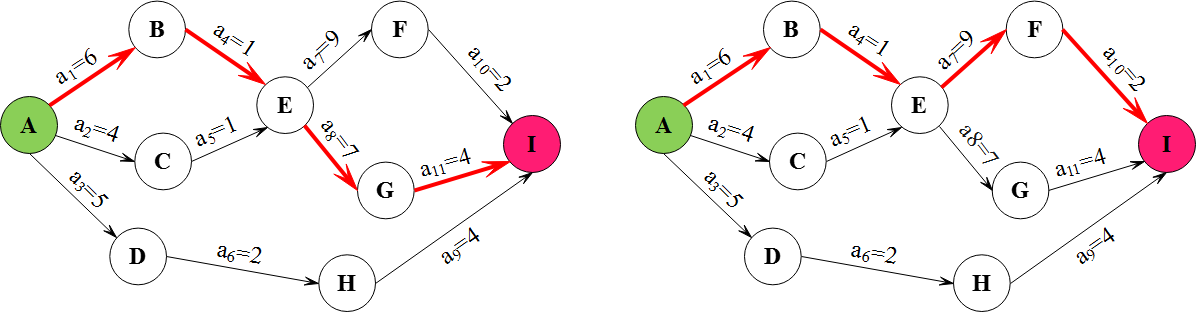
【算法分析】
本问题本质上就是利用AOE-网求关键路径的问题。AOE-网在工程计划和经营管理中有广泛的应用，针对实际的应用问题，通常需要解决以下两个问题：
（1）估算完成整项工程至少需要多少时间；
（2）判断哪些活动是影响工程进度的关键。
工程进度控制的关键在于抓住关键活动。在一定范围内，非关键活动的提前完成对于整个工程的进度没有直接的好处，它的稍许拖延也不会影响整个工程的进度。工程的指挥者可以把非关键活动的人力和物力资源暂时调给关键活动，加快其进展速度，以使整个工程提前完工。

【算法代码】

#include <bits/stdc++.h>
using namespace std;

typedef pair<int,int> PII;
const int maxn=211;
int val[maxn],e[maxn],ne[maxn],h[maxn],idx;
int in[maxn], cpin[maxn];
int q[maxn];
int ans;

int n,m;

void add(int a,int b,int w) {
	val[idx]=w,e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

bool topSort() {
	int head=0, tail=0;
	for(int i=1; i<=n; i++) {
		if(in[i]==0) q[tail++]=i;
	}
	while(head<tail) {
		int t=q[head++];
		for(int i=h[t]; i!=-1; i=ne[i]) {
			in[e[i]]--;
			if(in[e[i]]==0) q[tail++]=e[i];
		}
	}
	return tail==n;
}

vector<PII> path;
set<PII> s;
void dfs(int u, int cost) {
	if(h[u]==-1) {
		if(ans<=cost) {
			if(ans<cost) s.clear();
			ans=cost;
			for(int i=0; i<path.size(); i++) {
				s.insert(path[i]);
			}
		}
	}
	for(int i=h[u]; i!=-1; i=ne[i]) {
		path.push_back({u,e[i]});
		dfs(e[i],val[i]+cost);
		path.pop_back();
	}
}

int main() {
	while(cin>>n>>m) {
		memset(h,-1,sizeof(h));
		memset(in,0,sizeof(in));
		ans=0;
		while(m--) {
			int a,b,w;
			cin>>a>>b>>w;
			add(a,b,w);
			in[b]++;
		}

		memcpy(cpin,in,sizeof(in));
		if(topSort()) {
			for(int i=1; i<=n; i++) {
				if(cpin[i]==0) dfs(i,0);
			}
			cout<<ans<<endl;
			for(auto t:s) {
				cout<<t.first<<"->"<<t.second<<endl;
			}
		} else cout<<"No Solution."<<endl;
	}

	return 0;
}


/*
in:
9 11
1 2 6
1 3 4
1 4 5
2 5 1
3 5 1
4 6 2
5 7 9
5 8 7
6 8 4
7 9 2
8 9 4

out:
18
1->2
2->5
5->7
5->8
7->9
8->9
*/

【参考文献】
https://blog.nowcoder.net/n/20ddbcbe3a274052afdac2dd62c6e08f
https://blog.csdn.net/Keep_Trying_Go/article/details/126465446
https://www.acwing.com/solution/leetcode/content/62822/
https://blog.csdn.net/qq_42107348/article/details/125812306