题目:10.正则表达式匹配
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
示例 1:
输入:s = "aa", p = "a" 输出:false 解释:"a" 无法匹配 "aa" 整个字符串。
分析:
一开始看这道题目,可能会被以前做过的一道题误导,就是 '*' 可以匹配0个或多个字符,nonono~,看清后才知道原来是匹配0个或多个前面的那一个元素,第一次就因为粗心大意被坑了,但这道题我还是没解出来,看了多个题解也不是很明白,最后看到了某个大佬的题解,回溯法!下面就来带大家如何完成这道困难题吧!
首先我们可以在主函数上外包给我们的函数 back() 去完成:
return back(s, p, 0, 0);
// back()就是我们的回溯函数,s和p分别代表题目给定的字符串s、p,0、0代表目前的下标位置i和j下面就来简单构造一下back函数的大体结构:
我们可以先看作两个大的分支:一个是一定成功匹配,一个是不一定成功匹配。
一、一定成功匹配,就是s[i] == p[j],i和j是当前下标位置,或者p[j] == '.',因为 '.' 能匹配任意一个字符。成功匹配我懂,但是为什么还有不一定成功匹配?
二、不一定成功匹配,就是s[i] != p[j] 同时 p[j] != '.',但是,我们的p[j] 可能等于 '*' 呀,所以还是有余地的,不然就直接return false吧。
所以大体的框架就是:
bool back(string s, string p, int i, int j)
{
// 预留递归的出口
// 回溯处理
if (s[i] == p[j] || p[j] == '.')
{
if (j + 1 < p.size() && p[j+1] == '*'){
}else{
}
}else{
if (j + 1 < p.size() && p[j+1] == '*'){
}else{
return false;
}
}
}现在的问题是如果是s[i] == p[j] || p[j] == '.',那就正常的递归下一个,也就是s[i+1]、p[j+1],如果是 p[j] == '*' ,那就复杂了,但这也是关键点,我们来分析一下有几种状况:
一、复制
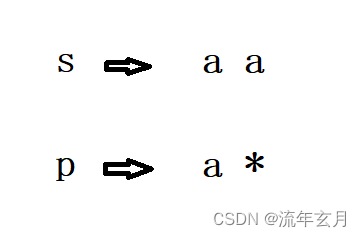
这里的 '*' 代表了复制的意思,那么问题就变成了 s[i+1] 和 p[j] 是否匹配的问题了,因为是 s[i] 已经和 p[j] 相同了,就看后面的是不是相同的字符,所以这里可以递归 back(s,p,i+1,j);
二、终止复制
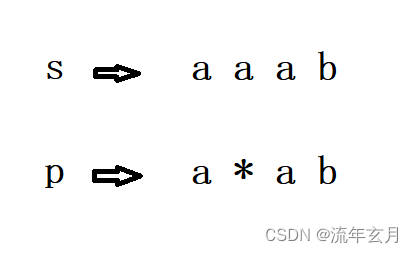
当 '*' 复制时,我们不能一直复制下去,不然最后就剩下 'b' 和 'ab' 匹配了,所以我们应该终止匹配,如何终止,可以用 s[i+2] 和 p[j+2] 匹配,所以就是 back(s,p,i+2,j+2) 了吧,错!应该是 back(s,p,i+1,j+2)!
为什么是 i+1 ?一开始我也想了很久,下面是我的个人观点:因为我们不确定是否需要终止复制,所以是在复制之后才开始终止复制,而不是一开始就终止复制,所以是执行了back(s,p,i+1,j) 再终止复制, 此时就相当于 back(s,p,i+1+1,j+2),也就是 s[i+2] 和 p[j+2] 的比较,如果是i+2,就是 s[i+3] 和 p[j+2] 的比较了。(如果有不同意见的可以再留言区指证)
三、越过
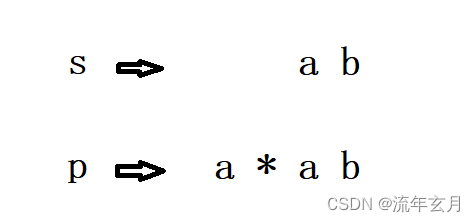
当 '*' 是消除的意思时,我们就需要越过 '*' ,把a当作0个去掉,这时候就是 s[i] 和 p[j+2] 匹配比较了,也就是 back(s,p,i,j+2);
按照上面的逻辑,我们可以推出代码:
bool back(string s, string p, int i, int j)
{
// 出口
// 回溯处理
if (s[i] == p[j] || p[j] == '.')
{
// 复制+复制终止+越过
if (j + 1 < p.size() && p[j+1] == '*'){
return back(s, p, i+1, j) || back(s, p, i+1, j+2) || back(s, p, i, j+2);
}else{
return back(s, p, i+1, j+1);
}
}else{
// 还有机会,p[j+1]是'*',可能是越过
if (j + 1 < p.size() && p[j+1] == '*')
return back(s, p, i, j+2);
else
return false;
}
}接下来就是怎么推出递归:
我们需要在题目中添加全局变量sn、pn来记录字符串s、p的长度,用size()也可以,当需要匹配的字符串 s 的 i 下标到 sn 时,就说明 sn 已经匹配完了,所以要判断 j 是否也匹配到结尾了,这时就有两种情况:一、j 正常到 pn,二、j 未到 pn。
如果 j 未到 pn 就返回错误了吗?未必,看下面的情况:
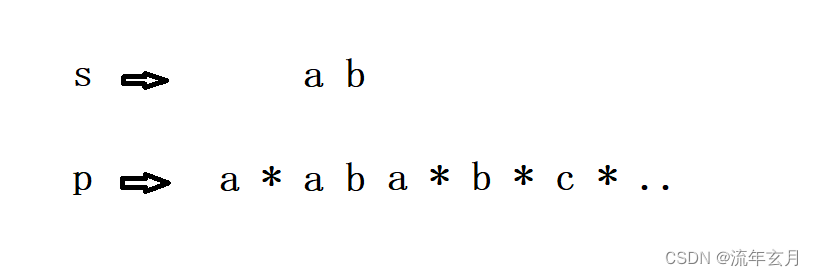
如果后面的 'x*x*' 的格式,就等于越过的意思,所以我们在 return 时要再次递归越过式,最后,如果 i == sn 不成立,但 j == pn 成立了,那说明字符串 p 已经结束而 s 未结束,所以是false的。下面来看看代码:
class Solution {
int sn;
int pn;
public:
bool back(string s, string p, int i, int j)
{
// 出口
if (i == sn)
return j == pn || (j+1<pn&&p[j+1]=='*'&& back(s,p,i,j+2));
else if (j == pn)
return false;
// 回溯处理
if (s[i] == p[j] || p[j] == '.')
{
// 复制+复制终止+越过
if (j + 1 < p.size() && p[j+1] == '*'){
return back(s, p, i+1, j) || back(s, p, i+1, j+2) || back(s, p, i, j+2);
}else{
return back(s, p, i+1, j+1);
}
}else{
// 还有机会,p[j+1]是'*',可能是越过
if (j + 1 < p.size() && p[j+1] == '*')
return back(s, p, i, j+2);
else
return false;
}
}
bool isMatch(string s, string p) {
sn = s.size(), pn = p.size();
return back(s, p, 0, 0);
}
};按道理来说,到这里已经结束了,but!力扣跟新了例子,发现会超时,那怎么办呢?
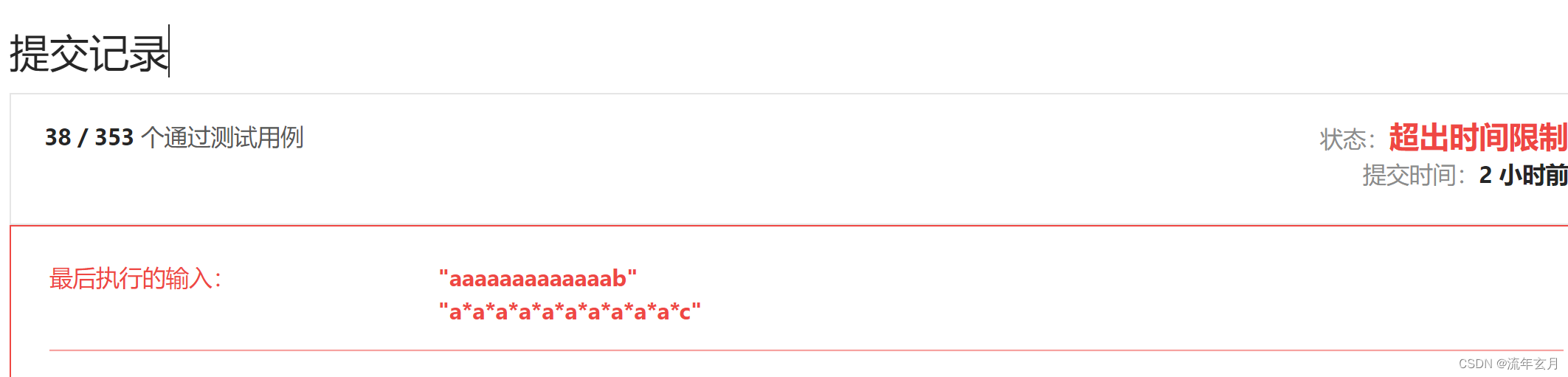
超出时间范围,很明显我们做了许多重复的操作,使其开销过大,所以我们需要定义一个二维数组或者向量来记录我们所到的地方是否正确,如果有错误,就说明已经判断过这个地方并且赋值了false,就可以上来就 return 掉,可以节省很多的时间及资源。
我们可以创建一个 dp[][] 长度需要预留多一位,可以有效避免访问出错,随后就把原先该得到的值先存到 dp[i][j] 当中,再 return dp[i][j], 所以改良后的代码如下:
class Solution {
int sn;
int pn;
vector<vector<bool>> memo;
public:
bool back(string s, string p, int i, int j)
{
// 记忆化减枝
if (memo[i][j] == false)
return false;
// 出口
if (i == sn){
memo[i][j] = j == pn || (j+1<pn&&p[j+1]=='*'&& back(s,p,i,j+2));
return memo[i][j];
}
else if (j == pn){
memo[i][j] = false;
return memo[i][j];
}
// 回溯处理
if (s[i] == p[j] || p[j] == '.')
{
// 复制+复制终止+越过
if (j + 1 < p.size() && p[j+1] == '*'){
memo[i][j] = back(s, p, i+1, j) || back(s, p, i+1, j+2) || back(s, p, i, j+2);
return memo[i][j];
}else{
memo[i][j] = back(s, p, i+1, j+1);
return memo[i][j];
}
}else{
// 还有机会,p[j+1]是'*',可能是越过
if (j + 1 < p.size() && p[j+1] == '*'){
memo[i][j] = back(s, p, i, j+2);
return memo[i][j];
}else{
memo[i][j] = false;
return memo[i][j];
}
}
}
bool isMatch(string s, string p) {
sn = s.size(), pn = p.size();
memo = vector<vector<bool>>(sn+1,vector<bool>(pn+1,true));
return back(s, p, 0, 0);
}
};执行后就可以通过啦!
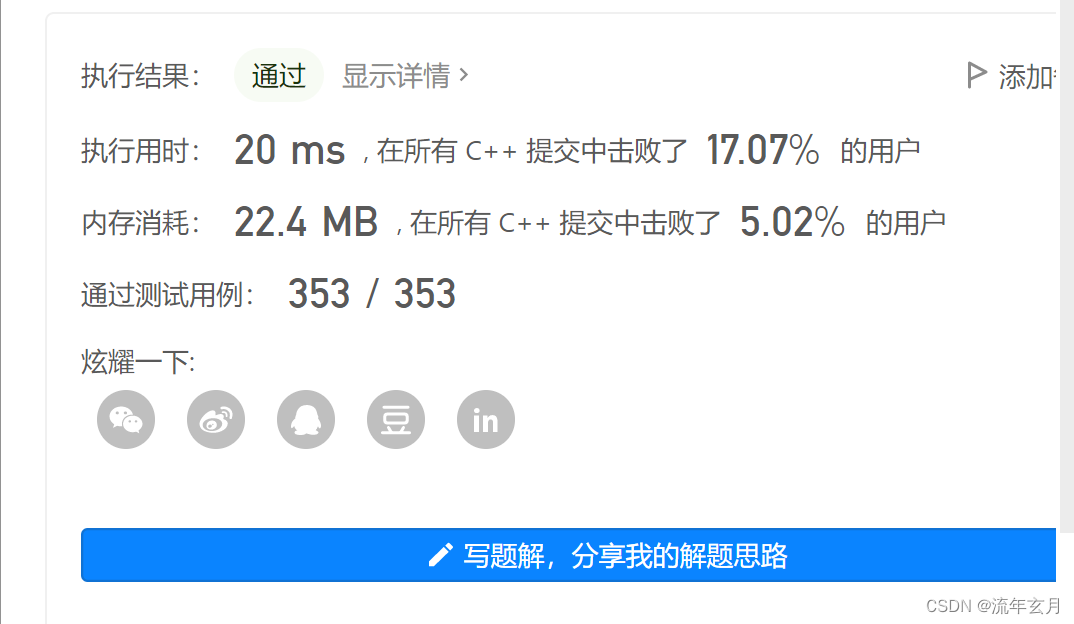








![[SpringBoot] AOP-AspectJ 切面技术](https://img-blog.csdnimg.cn/5726ce2133414fe596d8d38f34d9795e.png)