目录

前言

树的属性 

树的实现

树的遍历与应用

深度有限遍历 (DFS)

广度优先遍历 (BFS) 

---

Not all roots are buried down in the ground, some are at the top of a tree.

— Jinvirle

前言

Tree 是一些结点的集合，这个集合可以是空集；若不是空集，则 Tree 是由称为 根 的结点 r 以及零或多个非空的子树 T1,T2,⋯ ,​ 组成，这些子树的根都与 r 有一条有向边 (edge) 连接。这些子树的根被称为根 r 的孩子 (child)，而 r 是这些 child 的父亲 (parent)。 

树的属性 

根据给出的树的递归定义，可以发现一个树是由 N 个 node 和 N−1 条 edge 的集合。而除 root 外的所有 node 都有一个由其 parent 指向它的 edge。在树中有一些特殊的属性是需要注意的，这里先给出相关概念与示例，如果不是很理解，可以通过结合示例来理解这些概念。

结点的度 (degree)

        一个节点含有的子树的个数称为该节点的度

树的度 (degree of tree)

        一棵树中最大的 node degree 称为树的度

叶结点 (leaf)

        或称终端结点，如果结点满足 degree=0 则该结点为叶结点

分支结点 (branch node)

        或称内部结点 (internal node)、非终端结点，度不为 0 的结点

层次 (level)

        从 root 开始，root 所在的层为第 1 层，root 的 child 为第二层，以此类推

关系

        树就像一本族谱，从 root 开始结点直接有一定的亲缘关系

• 兄弟 (sibling): 具有相同父节点的节点互为兄弟节点
• 叔父 (uncle): 父结点的兄弟结点为该结点的叔父结点
• 堂兄弟: 父结点在同一层的结点互为堂兄弟

 

路径 (path)

结点 n1,n2,⋯ ,nk​ 的一个序列，使得对于 1≤i<k 满足 ni 是 ni+1 的 parent，则这个序列被称为从 n1​ 到结点 nk​ 的 path。其路径长度 (length) 为路径上的 edge 的数量，即 k−1 。特别地，每个结点到自己的 path lenth 为 0

深度 (depth)

对于结点 ni​ ，从 root 到 ni​ 的唯一路径的长度 (Depthroot=0)

高度 (height)

对于结点 ni​ ，从 ni 到 leaf 的最长路径长度 (Heightleaf=0)

树的高度

或称树的深度，其总是等于根的高度，或最深的结点的深度，可以认为一棵空树的高度为 −1

祖先 (ancestor)

对于结点 ni 与 nj 存在一条 ni​ 到 nj​ 的路径，那么称 ni​ 是 nj​ 的祖先 (ancestor)，而 nj​ 是 ni 的 后裔 (descendant)

距离 (distance)

对于结点 ni​ 与 nj ，从最近的公共祖先结点 nk​ 分别到它们的路径长度之和被称为距离 (distance)。特别地，如果 ni=nk​ ，则 ni 与 nj 的距离为 ni​ 到 nj 的路径的长度

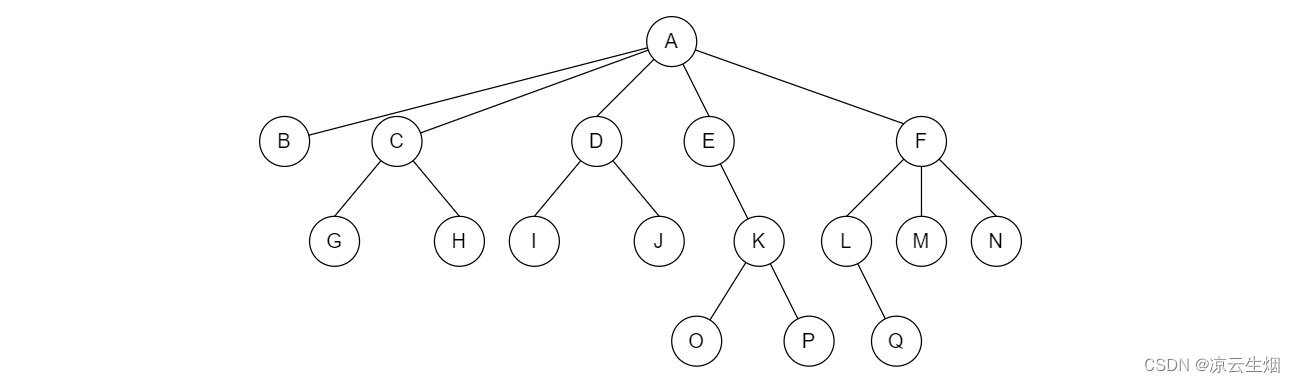
 注：

 严蔚敏老师的数据结构中，或者往常的实现中，根的高度为 1，而叶的深度也为 1，树的高度一般指其最大的层次，因此认为空树的高度为 0。

 树的实现

实现树的一种方法是在每一个结点上，除数据外还需要一些链域来指向该结点的每个子结点，然而由于每个结点的子结点数量是不确定的，我们不能直接建立到各个子结点的直接链接。如果申请一定大小的空间以存放子结点，则可能会造成空间的浪费，或不足。因此我们链表的形式存储子结点，而父结点中只存储第一个子结点的指针，如果该链域为空则意味着该结点是叶结点 (degree=0。每个结点中存在一个指向其下一个兄弟的指针，为遍历父结点的所有孩子提供了方法，当该结点 next_sibling=nullptr 时意味着这是父结点的最后一个子结点。 

struct TreeBaseNode {
  TreeBaseNode* first_child;
  TreeBaseNode* next_sibling;
};
template <class Element>
struct TreeNode {
  Element data;
};

如果我们用这个结构实现上述图示的树，可以画一下其表示。

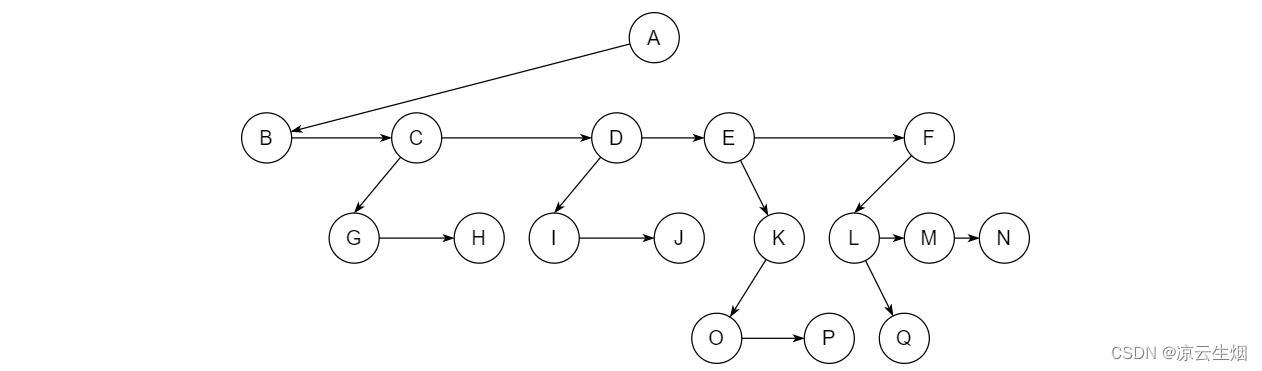
 可以发现，除非该结点是 leaf，否则我们很难判断该结点的 degree。且在计算深度与距离时，要十分小心在兄弟间步进，因为兄弟间步进并不会增加其与 parent 的距离。

树的遍历与应用

观察你系统中的文件系统，回到文件系统的顶层 / (root)，并浏览一些目录你会发现， 整个目录结构与 tree 是类似的，我们也常常将其称为目录树。

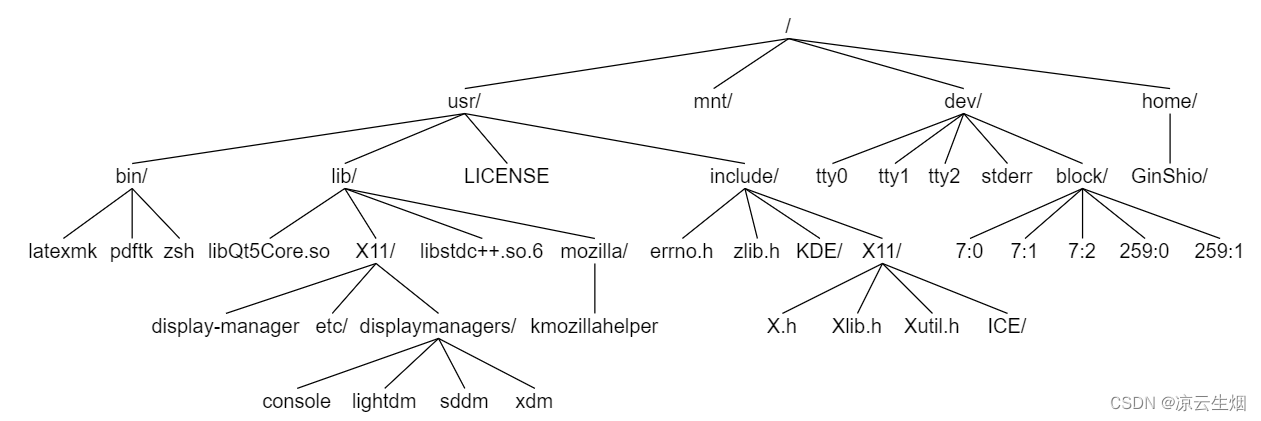
 这颗目录树稍微有些复杂了，不过问题不大。一般文件系统中采用路径名来访问一个文件，而我们可以像遍历树一样遍历这个文件系统，将每个文件打印出来，并按照层级来缩进文件名称。

深度有限遍历 (DFS)

给出一个代码实现：

void filesystem::list_all(file& f, int depth = 0) const {
  print_name(f, depth);  // 打印文件的名称
  if (is_directory(f)) {
    for (file p : get_file_list(f)) { // 遍历目录中的每个文件
      list_all(p, depth + 1);
    }
  }
}

最终的输出结果可能是：

/
 |--- mnt/
 |--- home/
       |--- GinShio/
 |--- usr
       |--- LICENSE
       |--- lib/
             |--- libQt5Core.so
             |--- X11/
                   |--- display-manager
                   |--- etc/
                   |--- displaymanagers/
                         |--- console
                         |--- lightdm
                         |--- sddm
                         |--- xdm
             |--- libstdc++.so.6
             |--- mozilla/
                   |--- kmozillahelper
       |--- bin/
             |--- latexmk
             |--- pdftk
             |--- zsh
.....
.....

在遍历中，每访问一个结点时，对结点的处理工作总是比其子结点的处理先进行，这种先处理根再处理子结点的策略被称为 前序遍历 (preorder traversal)。而另一种常用的遍历方法是 后序遍历 (postorder traversal)，即在结点的所有子结点处理完成后再对其进行处理。无论这两种遍历的哪一个，在遍历这个树时总是可以在 O(N) 的时间复杂度里完成。对于目录的 postorder traversal 留给读者思考并实现。

现在考虑这两种算法有什么共通的特点。有没有发现它们都是在一棵子树上处理完所有结点之后再转移到另一棵子树上，这种一直向着 child 递归，直到全部递归结束时再向 sibling 递归的算法，就被称之为 深度优先搜索 (Depth-first Search, DFS)。由于 DFS 使用递归算法，因此 DFS 总能被改写为 loop，非 tail recursion 的递归有可能需要 stack 的帮助才能改为 loop。

 

广度优先遍历 (BFS) 

请回看 树的实现 一节的图，图中的树如果以一层一层遍历，当一层的所有结点都被遍历完时，再进入更深一层，从这层的第一个结点开始处理。这种遍历方式被称为 广度优先遍历 (Breadth-first Search, BFS) 或者是层序遍历。