目录
- (前言1) 关于背景的回答:
- (前言2) 现有的降低噪声, 提高信噪比的一些特有方法的论文资料 (传统策略):
- 1. 关于波形反演与走时层析反演
- 2. 折射层析
- 3. 用一个合成数据来解释折射层析反演的思路
- 4. 其他层析反演方法:
- 5. 关于层析反演的一些TIPS (可补充)
- 参考文献:
降噪有关资料参考博客:
https://blog.csdn.net/qq_41033011/article/details/133279326?spm=1001.2014.3001.5502
https://blog.csdn.net/qq_52245889/article/details/133311238
https://blog.csdn.net/u014655960/article/details/133301825?spm=1001.2014.3001.5501
(前言1) 关于背景的回答:
-
传统的FWI的低频速度怎么获得的?
射线的层析成像 (应该是其中之一的手段?) -
传统的FWI的低频速度用处?
作为深部的初始速度模型, 可视作宏观速度. -
地震波的走时和振幅, 谁更容易产生噪声?
地震波的振幅. 因为一些情况下, 我们是可以设置走时时间的, 这样我们可以灵活删除和调整. 但是我们没有机会在地震波的振幅中进行类似操作. 任何旨在去除记录数据的非信号内容的信号处理都不可避免地会导致振幅失真 -
垂直撞击源相关的辐射能量由哪些构成?
瑞利型表面波和P-P、S-S、P-S和S-P波模式的混合波组成. -
近地表的速度模型是否重要? 为什么?
解析近地表速度模型是陆地成像的关键步骤,传统上是通过折射层析成像静力学来解决的. -
有什么手段可以估计近地表的数据?
利用走时层析 (traveltime tomography), 因为初至波中的折射部分总是能在无干扰的情况下最快到达地表, 可以安全假设为P波. 由此得到的模型可以很好地去表示近地表的近似.- 这个估计会很顺利吗?
1.并不一定, 近地表P波速度可以与空气中的声波一样低, 表层土甚至更低, S波速度可以低至100 m/S甚至更低.
这种低速度导致FWI方案的严重稳定性问题.
2.与地下不同, 近表面在性质上可能是高度不均匀的, 强烈各向异性的, 高度衰减的, 甚至是多孔弹性的. 因此, 如果不考虑近地表的这些特征, 全波弹性反演甚至是徒劳的。
- 这个估计会很顺利吗?
-
为什么一些地震记录中信噪比会偏低?
最直接的原因就是反射信号的频率和能量相比干扰信息要更低.
同时, 近地表的复杂地形也对信号有一定衰减和屏蔽作用, 这使得能量进一步下降. -
地震勘探中有哪些噪声?
相干噪声和不相干噪声这两大类
1.相干噪声: 包括面波, 折射波, 多次波等. 具有特定频率和特定视速度的噪声.
2.不相干噪声: 无特定频率和特定传播方向, 在地震记录上形成杂乱无章的干扰. 类似于随机噪声. -
低信噪比的地震记录的常规处理手段有哪些 (去噪或者增强有效信号)?
信噪比低主要是各种噪声导致的, 因此可以通过一些预处理与噪声抑制, 振幅补偿, 或者在反演过程中引入正则化项或额外约束条件.
(前言2) 现有的降低噪声, 提高信噪比的一些特有方法的论文资料 (传统策略):
1.论文: Full-waveform inversion and FWI imaging for land data
噪声影响振幅,那么便最大限度地减少幅度的影响, DMFWI给出的策略是多维局部相互关联, 他们说可以在强噪声环境下给出可靠结构.
2.论文: Application of 2D full-waveform inversion on exploration land data
从反演面波逐步过渡到面波与体波的结合, 在最后阶段表面波和体波一并融入一起参与反演.
面波被认定为干扰波, 但是面波的传播运动学以及动力学特征也包含了丰富的浅层地下介质信息, 因此也有专门基于面波的勘探方法.
面波在整个地震记录中呈现为一个近似三角形的形状, 能量非常强, 具有强振幅, 低频低速. 有时甚至将有效信号完全截断.
但是面波也具有频散的特性, 这一特性使得面波可以成为近地表速度反演的关键 [1] (下图红色说明的部分为面波, 它集中在距离炮点比较近的道集附近).

3.论文: A reality check on full-wave inversion applied to land seismic data for near-surface modeling
这是一个专注于弹性波的论文, 他认为利用声波做FWI是不对的.
而对于弹性波做FWI的困难, 他提出利用走时层析 (traveltime tomography) 来作为中间人.
弹性波做FWI的困难: The strategy to prevent full-wave elastic inversion of vertical-component geophone data trapped in a local minimum that results in a physically implausible near-surface model may be cascaded inversion.
一般的全波形反演未能很好收敛到速度模型, 这篇论文希望通过走时层析来估计的速度模型的高分辨率版本 (实现降噪). 即利用走时层析的反演结果作为初始模型, 并用它来做FWI.
具体的目标是:
1.走时层析成像来估计近地表的 P 波速度模型.
2.瑞利波反演来估计近地表的 S 波速度深度模型.
3.基于前两个初始模型做FWI.
这里之所以将近地表的P波速度估计与S波分离进行时因为: “上部近地表的P波和S波速度比可高达10或更多. 此外, 近表面S波速度场不一定是近表面P波速度场的缩放版本”.
由此, 可以认为, 通过走时层析反演来做好浅层地表结构识别是克服信噪比问题的一个很好的思路.
1. 关于波形反演与走时层析反演
在速度模型重建方面, 目前主要包括基本的
- 波形反演 和
- 走时层析反演 [2] 两大类
全波形反演方法基于波动理论, 具备反演高波数速度信息的能力 (应该就是高频信号, 就是更高分辨的部分), 但该方法对地震数据品质要求较高, 虽然在海洋资料处理中得到越来越多的应用, 但在陆地资料处理中仍无法大规模应用推广 (地上信噪比更低).
而走时类层析成像方法对数据品质要求低, 计算效率高, 是目前工业界的主要速度建模方法, 被广泛应用于建立近地表和深部速度结构模型 [3].
走时类层析成像方法一般分为: 利用 初至波 或者 折射波 来反演近地表速度结构, 利用长波长信息的准确性, 合理地反演近地表纵波速度 [4].
具体来说, 初至波包括:
- 直达波 (direct wave)
- 折射波 (refraction wave)
- 回折波 (diving wave)
(所以初至波和折射波实际上是一个包含和被包含的关系? 另外可以确定一点的是这三个波中折射波是最清晰的.)
初至波主要在近地表层进行传播, 一般能量较强, 便于识别, 且可追踪性好, 其走时包含了近地表层介质的速度信息. 一般我们通过初至拾取来获取这部分的信息.
另外关于折射波, 需要注意这里与物理学上折射的定义有所不同, 地震波的折射是指地震波沿着折射界面滑行, 从而产生折射波, 折射波传播速度指地震波在下伏地层的传播速度 [5].
2. 折射层析
折射层析成像法是通过对初至波进行射线追踪反演, 构建相应的速度层析成像图, 由此可以确定地质体中速度异常体的大小、位置、物性等参数 (说是"折射", 但是似乎并不单纯使用折射波, 而是全部的初至信息?).
折射层析成像法是基于相邻地层的速度差异, 对横向速度变化差异尤为敏感, 尤其适用于断层两盘有岩性差异的区域, 这些特点从一定程度上弥补了浅层地震反射法 (即以FWI为代表的波形反演) 的不足.
折射波走时层析成像主要步骤可分为四大部分 [ai]:
- 初至走时提取
- 建立初始速度模型
- 正演射线追踪
- 迭代反演
初至的正确拾取是折射层析反演工作的关键.
下面的右图是地震记录, 然后左图中红色箭头指向的颜色比较深的曲线是根据地震记录拾取初至后的 “时距曲线” , 而绿色是基于观察系统的初始速度模型进行正演得到的 “时距曲线”. 通过不断地正反演迭代, 两个曲线误差达到一定要求后, 导出此刻的速度模型为相应的 速度层析成像图 (这个过程和传统FWI似乎很像 … 如果我没记错, 传统FWI的误差计算是基于的整个记录).
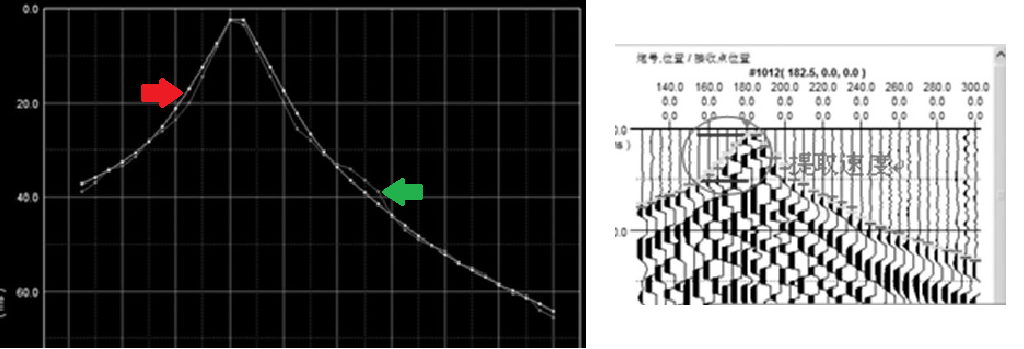
这个过程中, 初始速度模型的选取又变得至关重要.
初始模型与实际结果越接近, 层析反演计算速度越快, 效果越好. 过于简化的模型可能使结构中有意义的信息被忽略, 复杂的模型可能使反演的不确定性增强, 同时可能引入虚假信息 (层析反演与FWI是类似, 也是依赖于初始速度模型, 不可太清晰、不可太模糊).
折射层析成像过程中, 需对速度加以约束限制, 速度约束值范围越接近实际速度的变化范围反演效果越好. 在实际计算时, 应该根据测井资料以及速度谱等资料来确定速度约束值 (通过近期DL-FWI的实验经验, 即使是用神经网络拟合出地下的恰当速度范围也是很难的一件事).
综上不难确定, 折射层析成像的实质是反演, 即根据初至时间推断地下速度结构.
下图的右下角应该就是线性的初始速度模型.
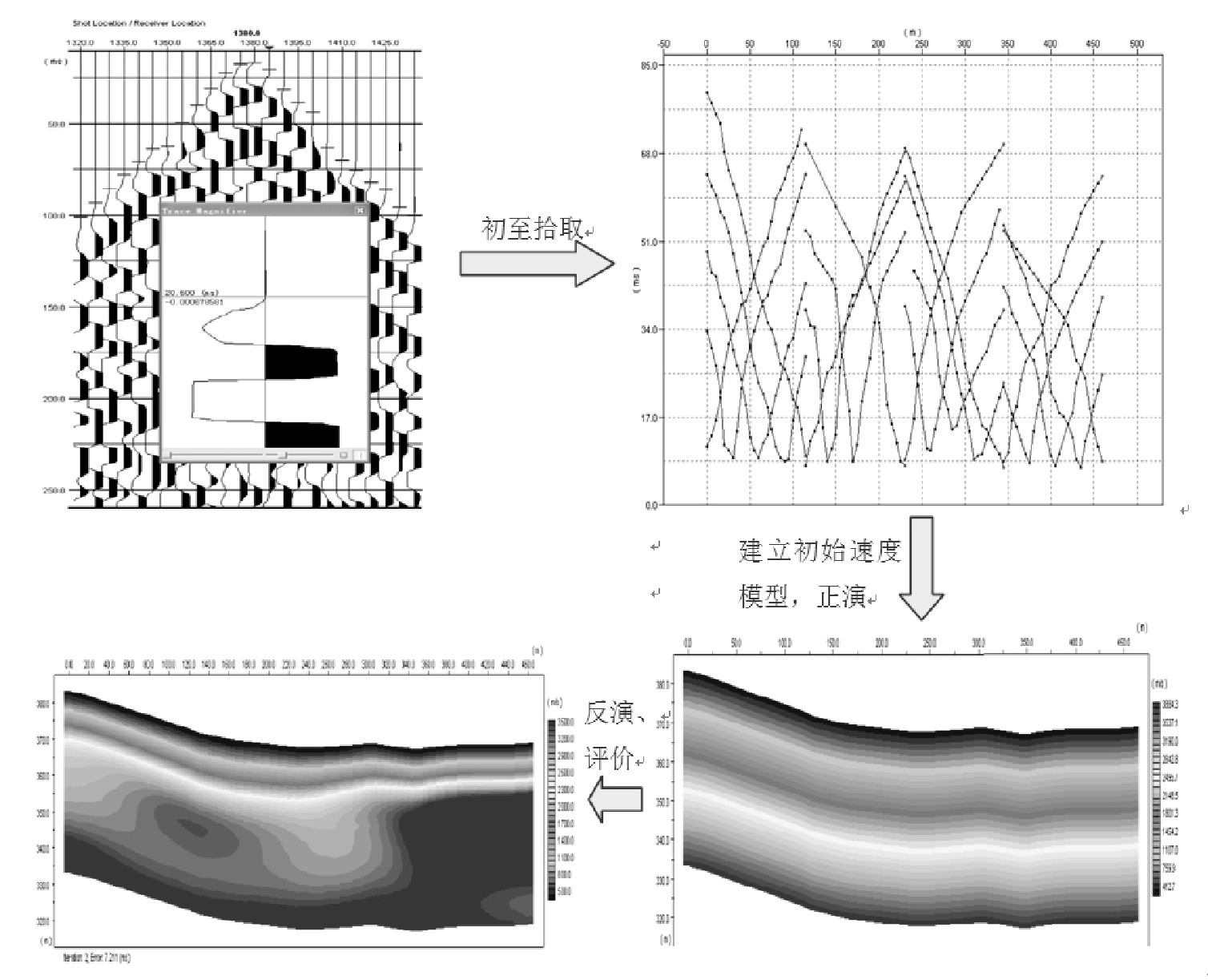
但是似乎要注意一个问题, 整个走时层析反演的正演都是采用一种 "射线追踪"的正演技术. 这就是为什么将其与以全波形反演为代表的"波形反演"区分开来.
射线追踪方法是基于射线理论的地震层析反演方法的基础, 是层析反演的正演过程中的关键技术, 其精度和效率直接影响层析反演的精度和效率. 近地表地震勘探的速度建模通常更为复杂, 包含起伏的崎岖地表和纵横向快速变化的速度结构等, 射线追踪正演方法更要有对复杂模型的高度适应性.
地震射线追踪方法的理论基础是斯奈尔定律、费马原理和惠更斯原理. 传统的射线追踪方法有试射法 (又称打靶法) [6] 和弯曲法 [7].
这两种方法的基本思想都是将波传播描述为射线前进, 射线追踪就是找到最小走时的射线前进路径. 缺点是计算精度和计算效率低, 以及在处理复杂模型时容易陷入局部最小值. 后来这类算法与Dijkstra算法结合产生了一类改进的直接进行射线追踪得到射线路径的最小走时算法 [8]. 而另一大类是将波传播描述为波前面扩展, 将求取射线路径的问题转化为求解波前面扩展的程函方程, 然后从接收点沿着波至时间梯度方向反向追踪得到射线路径. (更多传统的射线追踪的正演技术的数学原理请参考《朱怡诺. 折射波走时层析成像方法研究(学位论文)吉林大学》第三章 [9]) (但是如果我们要用DL来做, 是不是就不用特别深知射线追踪其中的内涵呢? )
此外, 似乎有一个现成的软件可以提供射线追踪正演的功能, 即Geogiga公司的Geogiga Seismic Pro. (但是这个软件似乎有点难搞到 ).
3. 用一个合成数据来解释折射层析反演的思路
首先本实验来源于《朱怡诺. 折射波走时层析成像方法研究(学位论文)吉林大学》
我在此列出一个实验案例来梳理方法思路.
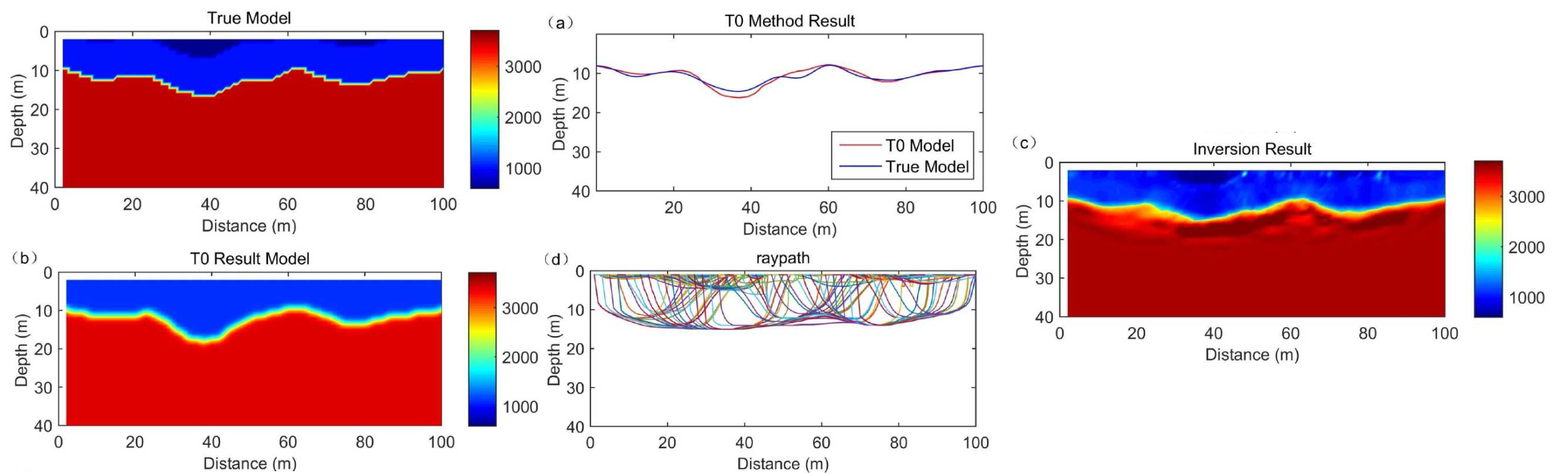
这里左上图代表一个合成数据, 也是目标地层. 而中上图是采用
t
0
t_0
t0差数法 [10] 得到的先验.
t
0
t_0
t0差数法等同于在每个检波点使用截距时间法 (ITM) [11] 来求取折射界面的深度, 而ITM适用于覆盖层和折射层较为平整的简单情况, 且在浅层界面误差较小, 但是在一些比较深且有薄夹层时误差比较大.
通过
t
0
t_0
t0差数法我们得到了浅层的主要折射面, 然后通过反距离梯度加权得到左下图的初始速度模型 (似乎就是上下给予速度的极值, 分界层给予速度中值, 并插值平滑了一下?).
然后在初始速度模型进行射线追踪的正演 (原文采用的是FMM [12] 和MSFM [13] 技术), 得到了中下图的射线路径. 可以发现, 得益于地震信息中折射波会伴随地层滑行, 它们似乎很好地刻画的界面结构. 同时, 近地表还有两个低速区, 虽然初次识别折射界面没有发现, 但是第二次迭代时, 这部分被射线正演发现了.
而后就是基于当前的射线信息进行反复迭代反演, 不断更新更准确的射线路径, 刻画并发现更多未被发现的浅层界面, 并且根据路径选择更好的速度模型, 这个思路类似于传统FWI. 最终迭代到损失较小时, 得到最终速度模型.
上述实验思路中, 我也持有一些疑问:
- 这里获取的第一个最大的折射界面的初始结构 是否是 在我们常规的地震资料中通过 初至波 获取的?
- 所谓浅层与深层的界线, 是否就是 t 0 t_0 t0差数法首次的折射深度为基准?
- 端到端的网络 是否可以 直接忽略中间的迭代, 同时也忽略射线技术, 直接通过 初至波 和 浅层界线以上的速度模型 来直接做拟合, 就如同DL-FWI那样?
我直觉感觉这三个回答是 yes.
4. 其他层析反演方法:
网格层析方法, 该方法基于数据驱动, 利用离散的矩形网格点对地下空间连续的介质剖分, 通过解析建立的矩阵方程来反演迭代局部的速度扰动, 在地层连续沉积、构造相对稳定的工区取得了较好的应用效果.
这种介质剖分通过相关的地质属性进行约束, 能有效求解解析矩阵 [14], 实现了更小尺度范围的速度求解, 精度高.
但是解矩阵方程及迭代更新需要大量的计算时间, 对计算机硬件的要求较为苛刻.
从反演角度讲, 网格剖分较大时每个网格内通过的射线越多, 越利于反演, 但从正演角度讲, 网格剖分过大则会降低正演精度, 从而直接影响反演的精度。实际计算时, 网格剖分要同时兼具两者才能取得更好的反演效果。
5. 关于层析反演的一些TIPS (可补充)
- 使用初至波的层析反演有个特点, 它的速度更新范围比较浅, 穿透深度多在 500 500 500~ 800 800 800m.
- 另一个问题是, 做好了浅层的估计后, 如何在进行其他更深例如中层的相关预测, 并考虑这些预测如何与浅层预测的融合. 毕竟, 仅仅考虑近地表的速度模型是远远不够的,更多的是要将整个速度模型的建立与成像方法综合起来进行研究.
- 常规的初至部分信号会受到低信噪比的影响, 而深度学习将会是处理这些信号的关键突破口.
参考文献:
[1] 伍敦仕,孙成禹,林美言.基于频率-速度域多重信号分类的面波高分辨率频散成像方法[J].石油物探,2017,56(01):141-149.
[3] Huang J, Zhao D. High-resolution mantle tomography of China and surrounding regions[J]. Journal of Geophysical Research Solid Earth, 2006, 111(B9).
[2] 徐嘉亮,周东红,贺电波等.高精度深度域层析速度反演方法[J].石油地球物理勘探,2018,53(04):737-744+652.DOI:10.13810/j.cnki.issn.1000-7210.2018.04.010.
[4] Siwei Li and Alexander Vladimirsky and Sergey Fomel.First-break traveltime tomography with the double-square-root eikonal equation[J].Geophysics,2013,78(6):U89-U101.
[5] 北京铀矿地质研究所浅层地震组.浅层地震探测方法与技术[M]. 北京:原子能出版社,1982:41-84.
[6] Engdahl E R. Relocation of Intermediate Depth Earthquakes in the Central Aleutians by Seismic Ray Tracing[J]. Nature, 1973, 245(141):23-25.
[7] Julian B R, Gubbins D. Three Dimensional Seismic Ray Tracing[J]. Geophysics, 1977.
[8] Moser, T.J. Migration Using the Shortest-Path Method. Geophysics, 1994, 59(7): p. 1110-1120.
[9] 朱怡诺. 折射波走时层析成像方法研究[D].吉林大学,2019.
[10] Hagedoorn J G. The Plus-Minus Method of Interpreting Seismic Refraction Sections[J]. Geophysical Prospecting, 1959, 7(2): 158-182.
[11] Ewing M, Woollard, Vine A C, et al. Geophysical investigations in the emerged and submerged Atlantic Coastal Plain: Part IV. Cape May, New Jersey, Section[J]. Geological Society of America Bulletin,1940, 51: 1821-1840.
[12] Sethian, J.A. A fast marching level set method for monotonically advancing fronts[J]. Proceedings of the National Academy of Sciences of the United States of America, 1996, 93(4): p. 1591-1595.
[13] Hassouna M S, Farag A A. MultiStencils Fast Marching Methods: A Highly Accurate Solution to the Eikonal Equation on Cartesian Domains[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(9):1563-1574.
[14] 张慧,李振春.基于双变网格算法的地震波正演模拟[J].地球物理学报,2011,54(01):77-86.