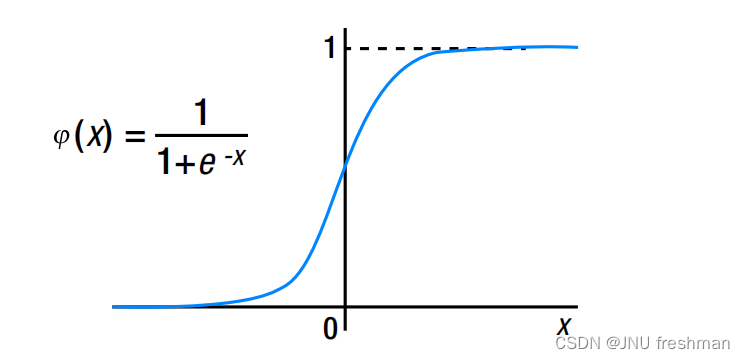
机器学习之广义增量规则(Generalized Delta Rule)
news2026/2/15 16:18:53
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1052682.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
案例突破——再探策略模式
再探设计模式 一、背景介绍二、 思路方案三、过程1. 策略模式基本概念2. 策略模式类图3. 策略模式基本代码策略类抽象策略类Context类客户端 4. 策略模式还可以进行优化的地方5. 对策略模式的优化(配置文件反射) 四、总结五、升华 一、背景介绍
在做项目…
ccf_csp第一题汇总
ccf_csp第一题汇总 printf()输出格式大全(附 - 示例代码)现值计算AcWing 4699. 如此编码AcWing 4509. 归一化处理(小数位数根号函数)AcWing 4454. 未初始化警告AcWing 4280. 序列查询AcWing 4006. 数组推导(小陷阱)AcWing 3292. 称检测点查询AcWing 3287…
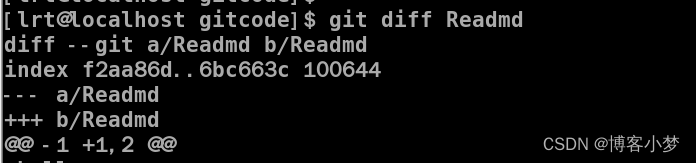
git你学“废”了吗?——git本地仓库的创建
git你学“废”了吗?——git本地仓库的创建😎 前言🙌初识gitgit 本地仓库的创建1、基于centos7环境下 git的下载2、设置自己的用户名和邮箱 查看.git中的结构区分清楚版本库和工作区 查看git中的相关内容查看仓库的状态 总结撒花💞…
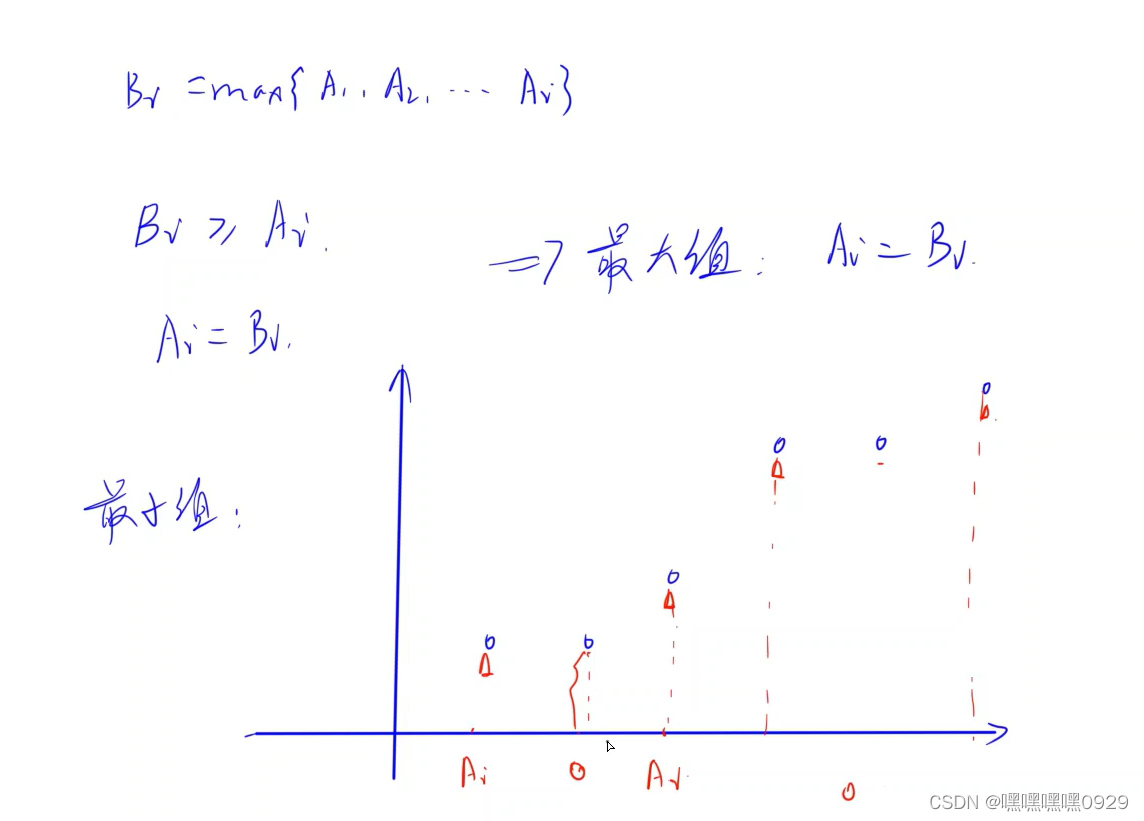
[题]修剪草坪 #单调队列优化
题目
洛谷上的题目 Acwing上的题目 根据y总的一波分析,我们得出……公式就是一切…… 所以,我要学会推公式…… 推公式…… 公式…… #include<bits/stdc.h>
using namespace std;
typedef long long ll; const int N 1e5 10;
int n, m;
ll s[N…
知识库系统都有哪些?知识库系统功能和介绍
知识库的建立是企业数字化转型的重要一步,能够为企业的可持续发展奠定坚实的基础。使用HelpLook创建的知识库知识库系统已经成为当前很多人的选择。 HelpLook可以实现并制作企业帮助中心设计、产品说明书、常见问题手册、在线知识库、企业文档制作。
点击注册使用&…
pip version 更新
最近报了一个错: 解决办法:
在cmd输入“conda install pip”
conda install pip 完了之后再输入:
python -m pip install --upgrade pip ok.
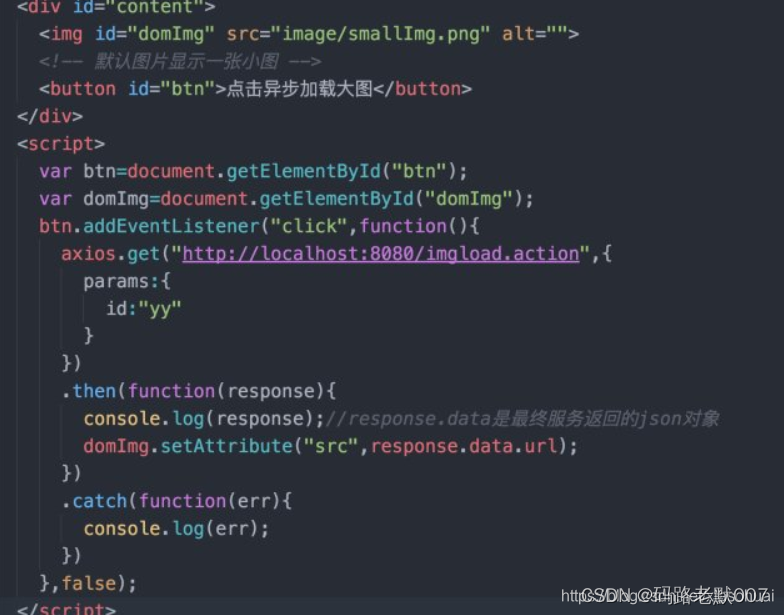
面试题六:Promise的使用,一文详细讲解
含义
Promise是异步编程的一种解决方案,比传统的解决方案(回调函数和事件)更合理更强大。
所谓Promise,简单说就是一个容器,里面保存着某个未来才会结束的事件 (通常是一个异步操作)的结果。从语法上说,P…
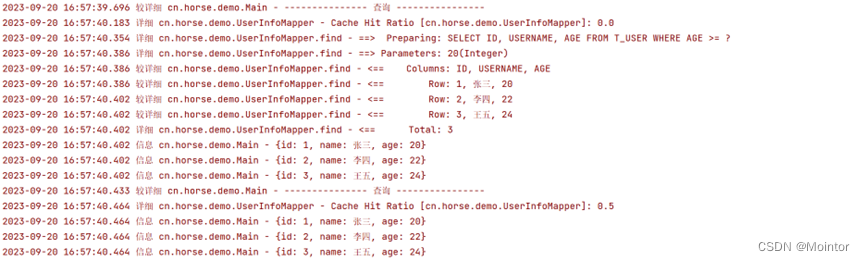
Mybatis 二级缓存(使用Redis作为二级缓存)
上一篇我们介绍了mybatis中二级缓存的使用,本篇我们在此基础上介绍Mybatis中如何使用Redis作为二级缓存。
如果您对mybatis中二级缓存的使用不太了解,建议您先进行了解后再阅读本篇,可以参考:
Mybatis 二级缓存https://blog.csd…
oracle分组合并数值带顺序
比如:有如下一张设备电子围栏位置坐标的表(tb_equ_point)。
equ_name:设备电子围栏名称
point_id:点位坐标id
point_x:点位x坐标
point_y:点位y坐标。 附数据:
INSERT INTO "tb_equ_point" ("EQU_NAME",…
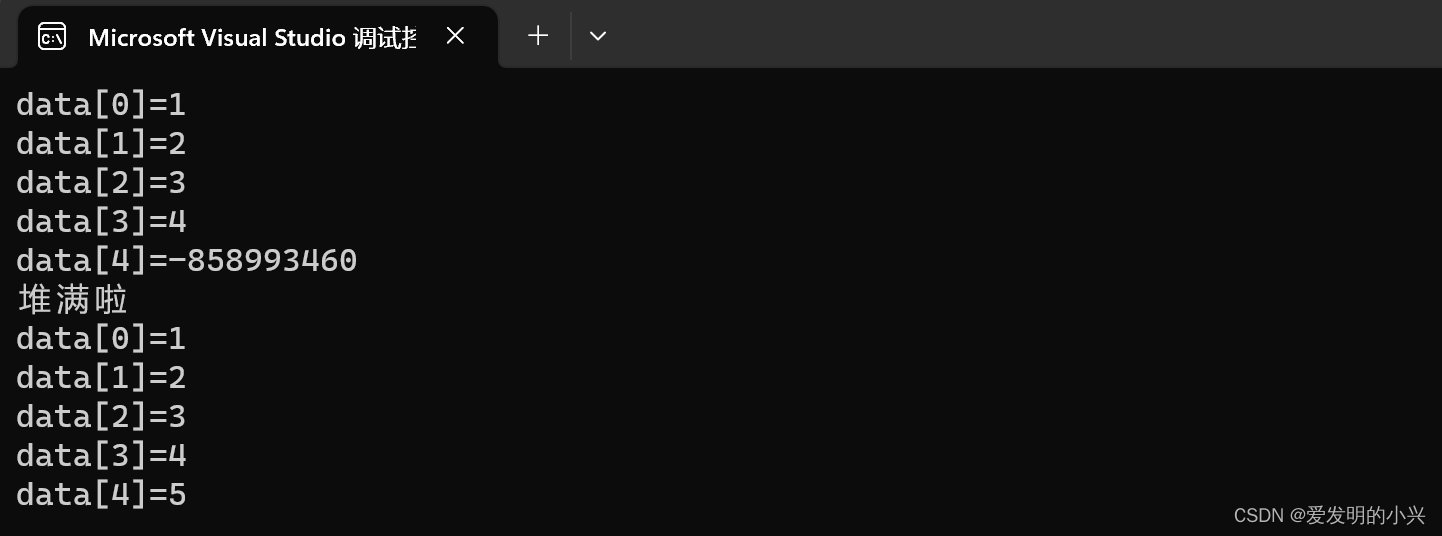
数据结构题型11-顺序队列
#include <iostream> //引入头文件
using namespace std;typedef int Elemtype;#define Maxsize 5
#define ERROR 0
#define OK 1typedef struct
{Elemtype data[Maxsize];int front, rear;
}SqQueue;void InitQueue(SqQueue& Q) //初始化队列
{Q.rear Q.front…
使用代理IP进行安全高效的竞争情报收集,为企业赢得竞争优势
在激烈的市场竞争中,知己知彼方能百战百胜。竞争对手的信息对于企业来说至关重要,它提供了洞察竞争环境和市场的窗口。在这个信息时代,代理IP是一种实用的工具,可以帮助企业收集竞争对手的产品信息和营销活动数据,为企…
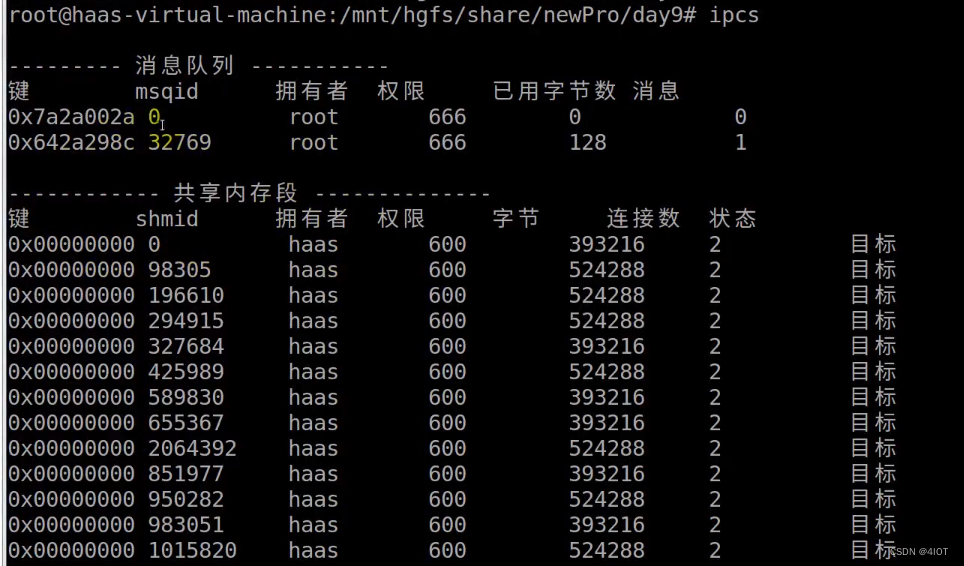
lv5 嵌入式开发-11 消息队列
掌握:消息队列机制、打开/创建消息队列、发送消息、接收消息
1 消息队列
消息队列是System V IPC对象的一种
消息队列由消息队列ID来唯一标识
消息队列就是一个消息的列表。用户可以在消息队列中添加消息、读取消息等
消息队列可以按照类型来发送/接收消息
消…
Win10自带输入法怎么删除-Win10卸载微软输入法的方法
Win10自带输入法怎么删除?Win10系统自带输入法就是微软输入法,这个输入法满足了很多用户的输入需求。但是,有些用户想要使用其它的输入法,这时候就想删除掉微软输入法。下面小编给大家介绍最简单方便的卸载方法吧。 Win10卸载微软…
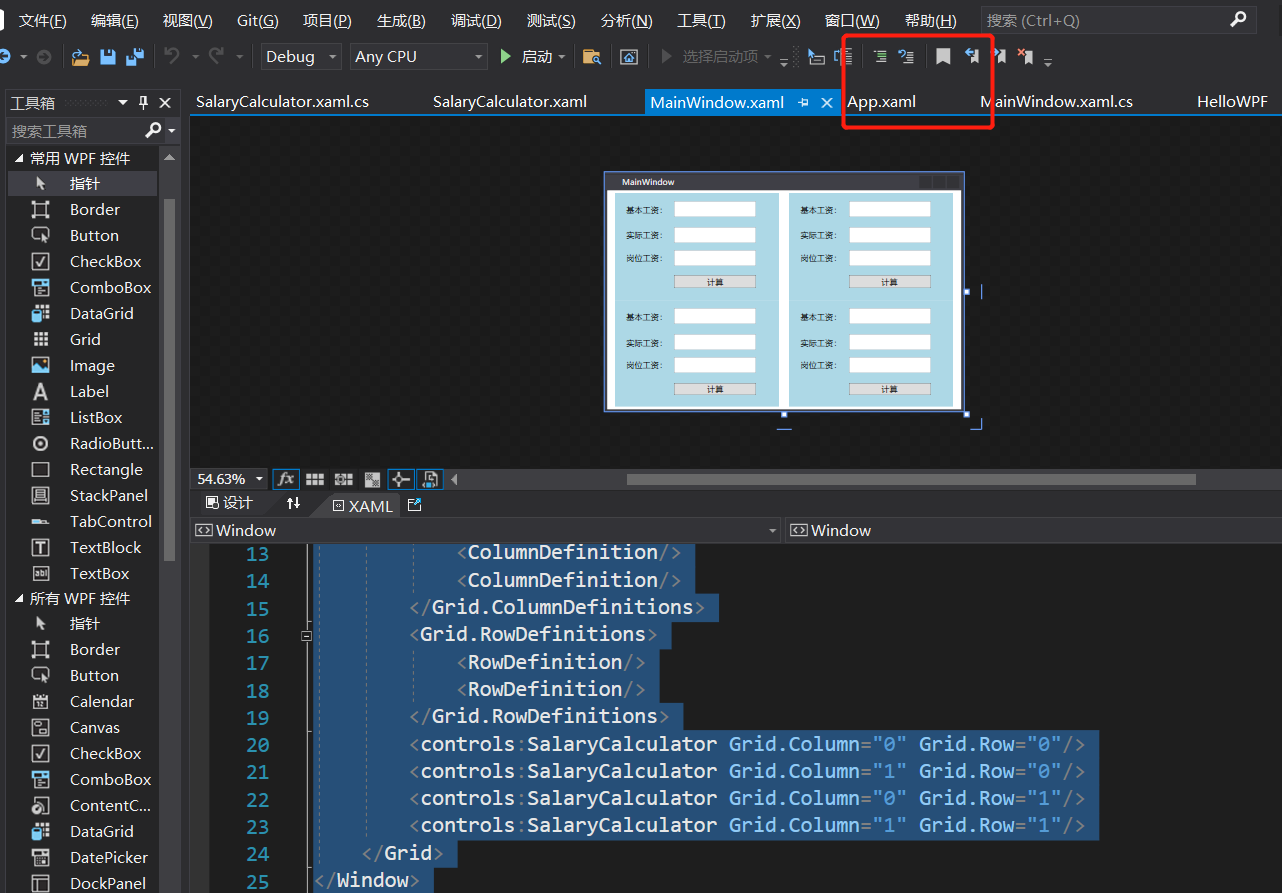
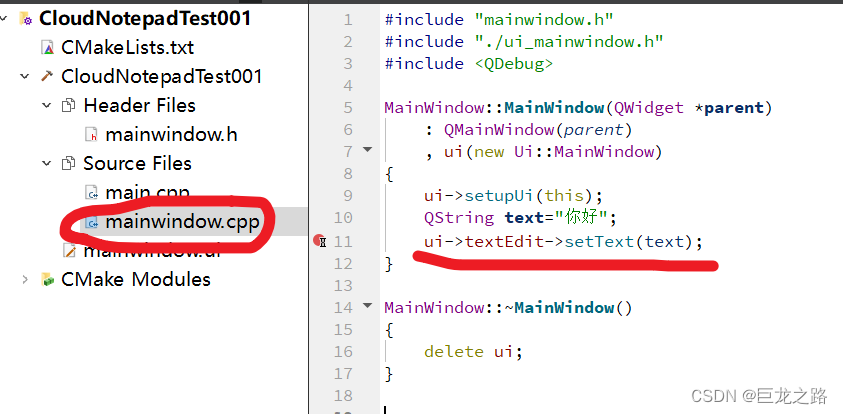
在Qt中,怎么获取到在mainwindow.ui文件中添加的控件
2023年9月30日,周六晚上 假设我在mainwindow.ui中添加了一个名为textEdit的QTextEdit对象 在mainwindow.cpp中,可以通过ui对象来获取到这个控件
妙不可言的Python之旅----(一)
初识Python
python的起源
1989年,为了打发圣诞节假期,Gudio van Rossum吉多 范罗苏姆(龟叔)决心开发一个新的解释程序(Python雏形)
1991年,第一个Python解释器诞生
Python这个名字ÿ…
怎么修改jupyter lab 的工作路径而不是直接再桌面路径打开
要修改Jupyter Lab的工作路径,你可以按照以下步骤操作:
打开终端或命令提示符窗口。
输入 jupyter lab --generate-config 命令来生成Jupyter Lab的配置文件。
找到生成的配置文件,通常会位于 ~/.jupyter/jupyter_notebook_config.py。
使…
C++ AB组辅导课
C AB组辅导课 蓝桥杯C AB组辅导课 第一讲 递归与递推 Acwing1、整数划分(递归)2、acwing92. 递归实现指数型枚举10凑算式(全排列)11李白打酒(全排列)12、棋牌总数(递归)13、剪邮票(递归)14、1050. 鸣人的影分身 (递归或动态规划(记忆化搜索))15、方格分割 (dfs思维&…


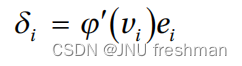
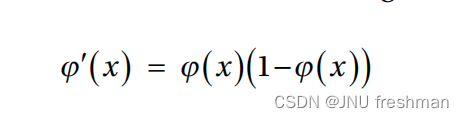
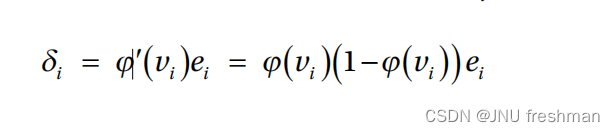
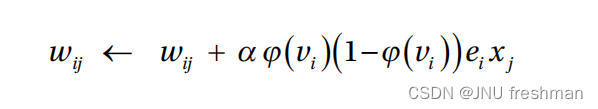


![[题]修剪草坪 #单调队列优化](https://img-blog.csdnimg.cn/20210201211628892.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NTkxNjk1OQ==,size_16,color_FFFFFF,t_70)