初识红黑树

news2024/11/28 7:39:09

文章目录

  • 1.红黑树的介绍
    • 1.0红黑树的来源
    • 1.1红黑树的概念
    • 1.2红黑树的性质
  • 2.红黑树构建示例
    • 2.1只变色
      • 1.祖父为根/不为根
      • 2.连续回溯
    • 2.2变色+旋转
  • 3.红黑树构建情况分类
    • 3.0默认插入结点颜色
    • 3.1情况一:变色
      • 1.未知树为空
      • 2.未知树不空
    • 3.2情况二:单旋+变色
      • 1.uncle不存在
      • 2.uncle存在为黑
    • 3.3情况三:双旋+变色
      • 1.uncle不存在
      • 2.uncle存在为黑
    • 3.4总结
  • 4.看图写代码[有手就行]
    • 4.1RedBlackTree.h
    • 4.2Test.cpp

在这里插入图片描述

1.红黑树的介绍

想了解红黑树,首先需要对AVL树有一定的认识.点击上篇博客浅浅学习一下吧~AVL树

1.0红黑树的来源

在这里插入图片描述
AVL树绝对平衡[左右高度不超过1]===>红黑树近似平衡–最长路径不超过最短路径的2倍
查找:AVL- logN 红黑树 logN~2logN
插入/删除:红黑树旋转次数较少

  1. 红黑树是因为AVL树在某种情况下不太优的情况下出现的.
  2. AVL树的查找、插入和删除T(n)==O(logn);但是每插入/删除操作后就需要对其进行旋转处理–成本高
  3. 为了找到一种更好的数据结构,1972年Rudolf Bayer发明了平衡二叉B树（symmetric binary B-trees）。1978年Leo J. Guibas 和 Robert Sedgewick 修改称“红黑树”。

1.1红黑树的概念

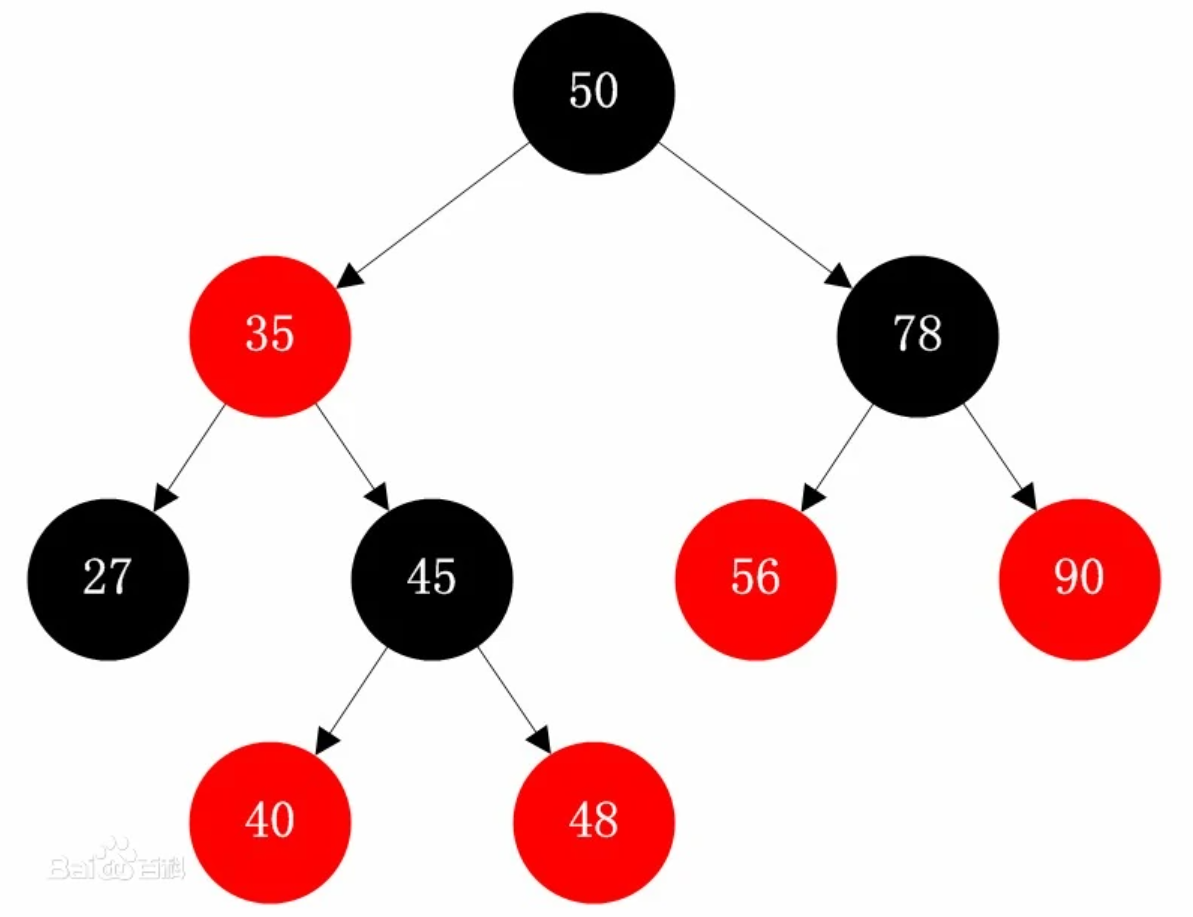
红黑树是一种自平衡的二叉查找树，不同的是在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径长度是其他路径的两倍，因而接近平衡。
因为以下这种情况:

二叉搜索树，插入数据随机时接近平衡二叉树，操作效率（查询，插入，删除）效率较高，时间复杂度是O（logN）。但是当插入数据有序（递增或者递减），那么所有节点都会在一侧，此时，二叉搜索树成了一个链表，操作效率降低了，时间复杂度为O(N).

出现了AVL树,但是AVL树每插入/删除都要旋转处理,成本高,于是出现了红黑树.需要注意的是:

红黑树具备了二叉搜索树的某些特性，它是一种接近平衡的二叉树（它没有AVL树平衡因子的概念，仅靠5条性质来维持一种接近平衡的结构）。

1.2红黑树的性质

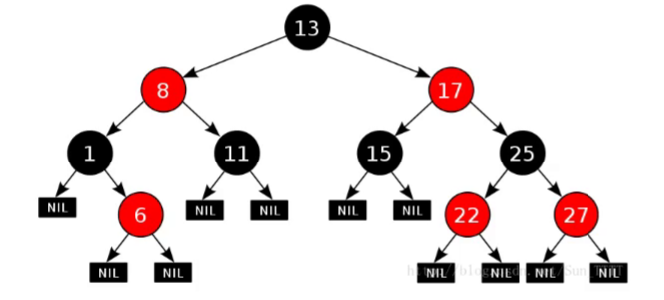
在这里插入图片描述

  1. 每个结点非黑即红
  2. 根节点为黑色
  3. 一个红色父结点的两个子结点均为黑色.[没有连续红节点][红色结点的父节点为黑色子结点为黑色][两个黑色结点的父结点不一定是红节点]
  4. 每个结点，从该结点到其所有后代叶结点的简单路径上，黑色结点个数相同[每条简单路径上都有相同个数黑节点]
  5. 空结点均为黑[计算结点个数不算空结点]

拓展性质

  1. 极限最短路径:全黑 极限最长路径:一黑一红
  2. 一棵红黑树接近满二叉树/单独取黑色结点也是接近满二叉树
  3. 假设黑色结点个数为N 整棵树结点数量[N, 2N]
  4. 最短路径logN 最长路径2logN
  5. 路径数目 == 根节点到空结点

思考：以上5条性质如何使得其最长路径中节点个数不会超过最短路径节点个数的两倍？

2.红黑树构建示例

插入一个红色结点可能会出现的情况

2.1只变色

1.祖父为根/不为根

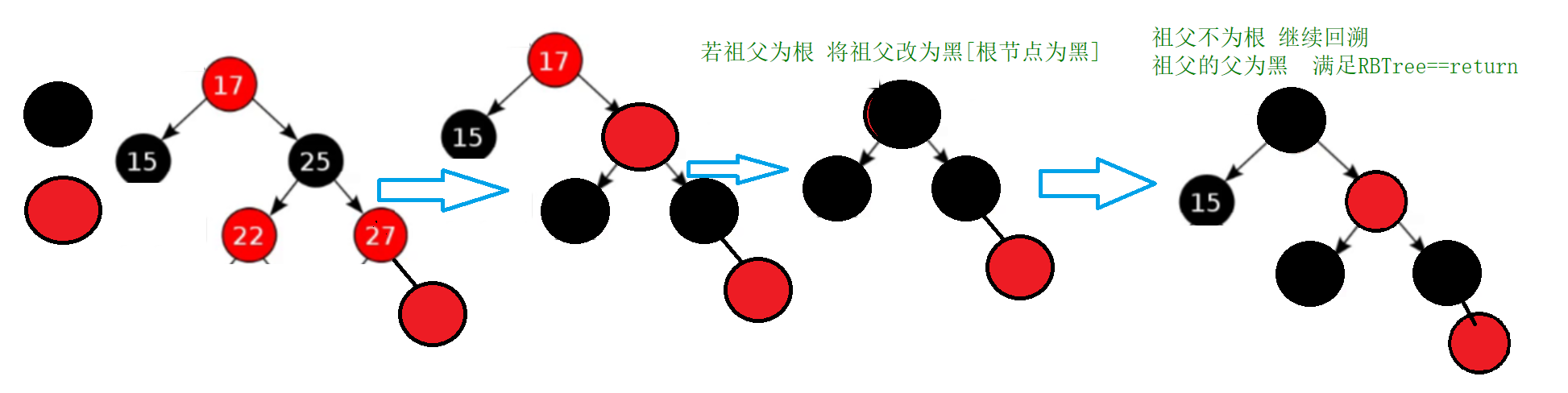
在这里插入图片描述

2.连续回溯

在这里插入图片描述

2.2变色+旋转

在这里插入图片描述

3.红黑树构建情况分类

3.0默认插入结点颜色

默认插入结点为红色

  1. 若为黑色 一旦插入违反性质4–error
  2. 插入红色 若父节点为黑不操作 若父节点为红需要操作–默认插入为红可以减少操作次数

3.1情况一:变色

1.未知树为空

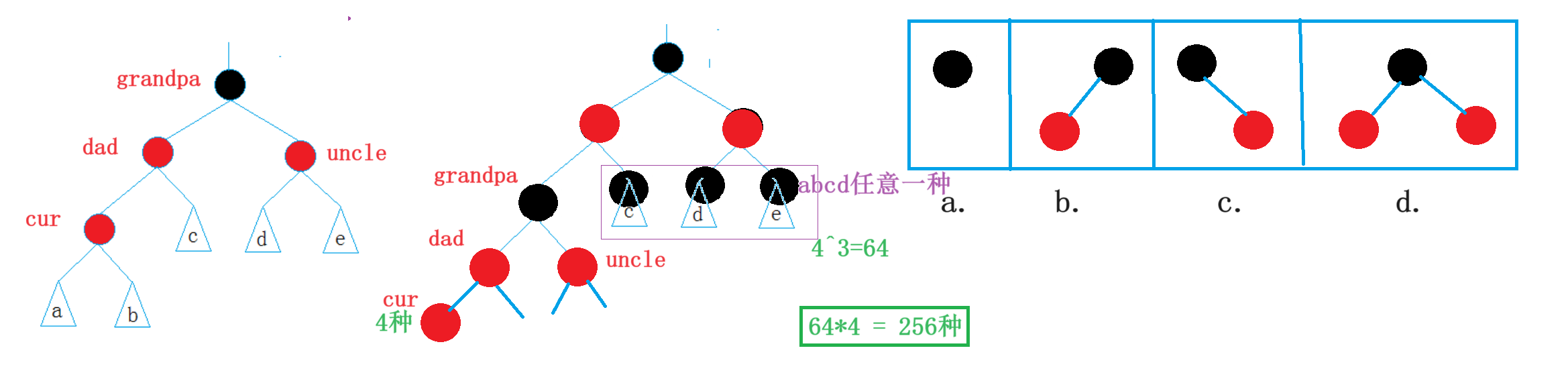
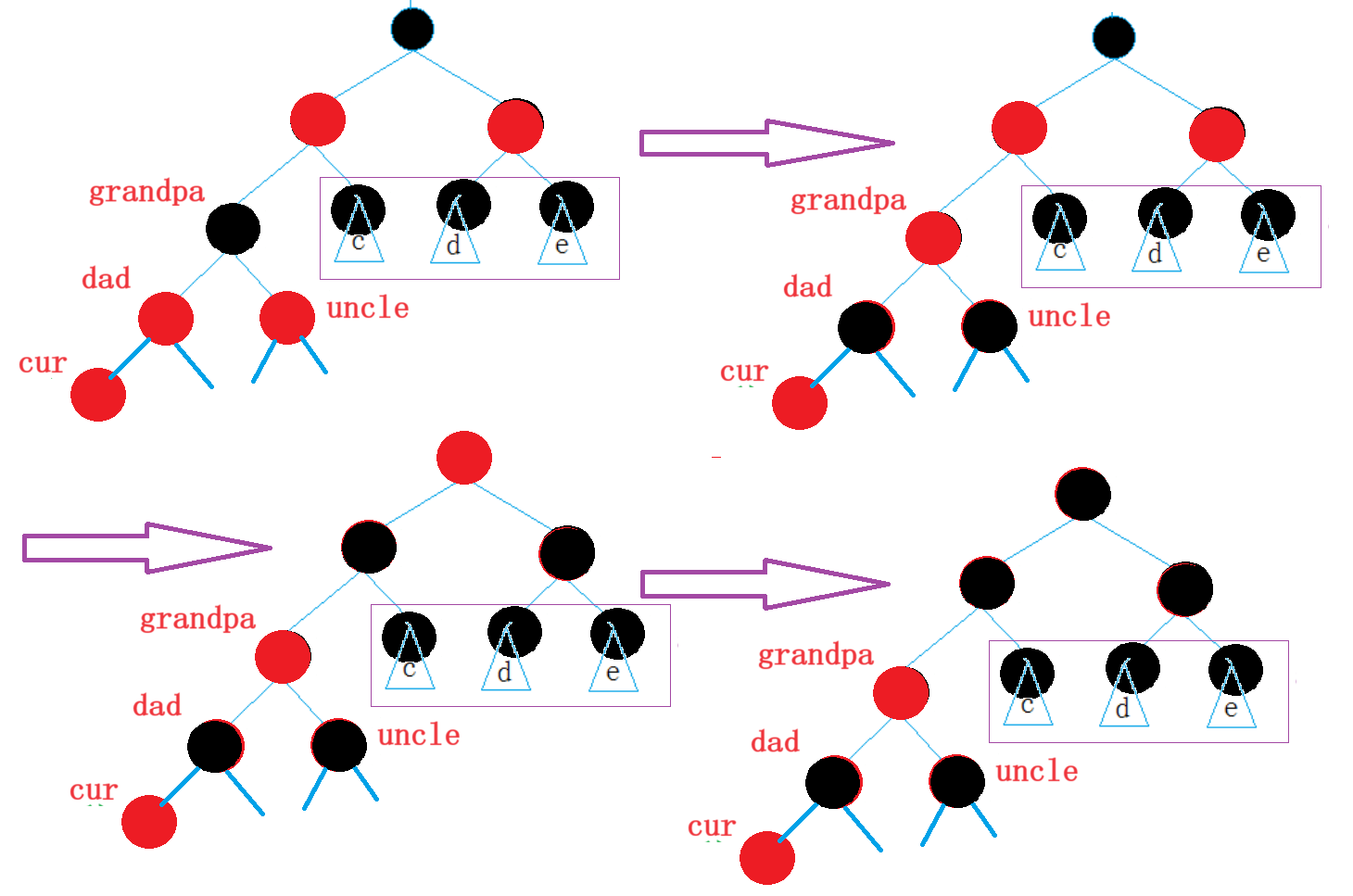
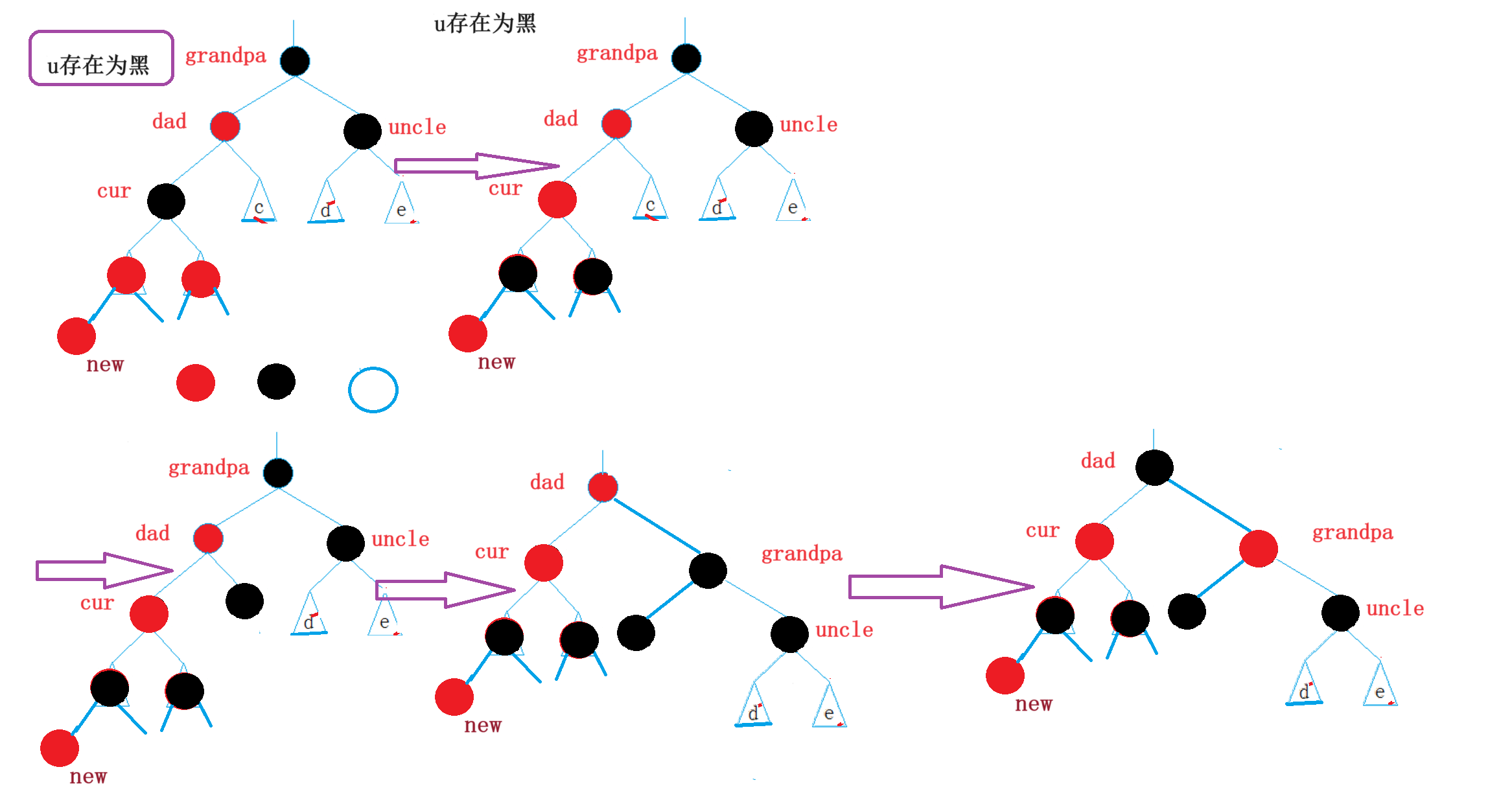
在这里插入图片描述

2.未知树不空

在这里插入图片描述

在这里插入图片描述

3.2情况二:单旋+变色

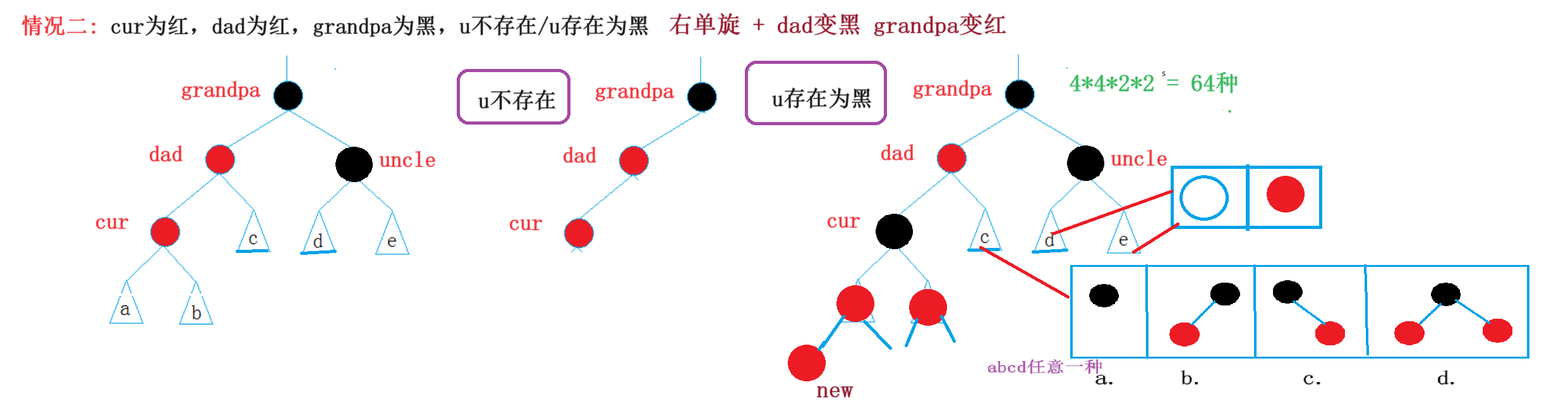
在这里插入图片描述

1.uncle不存在

在这里插入图片描述

2.uncle存在为黑

在这里插入图片描述

3.3情况三:双旋+变色

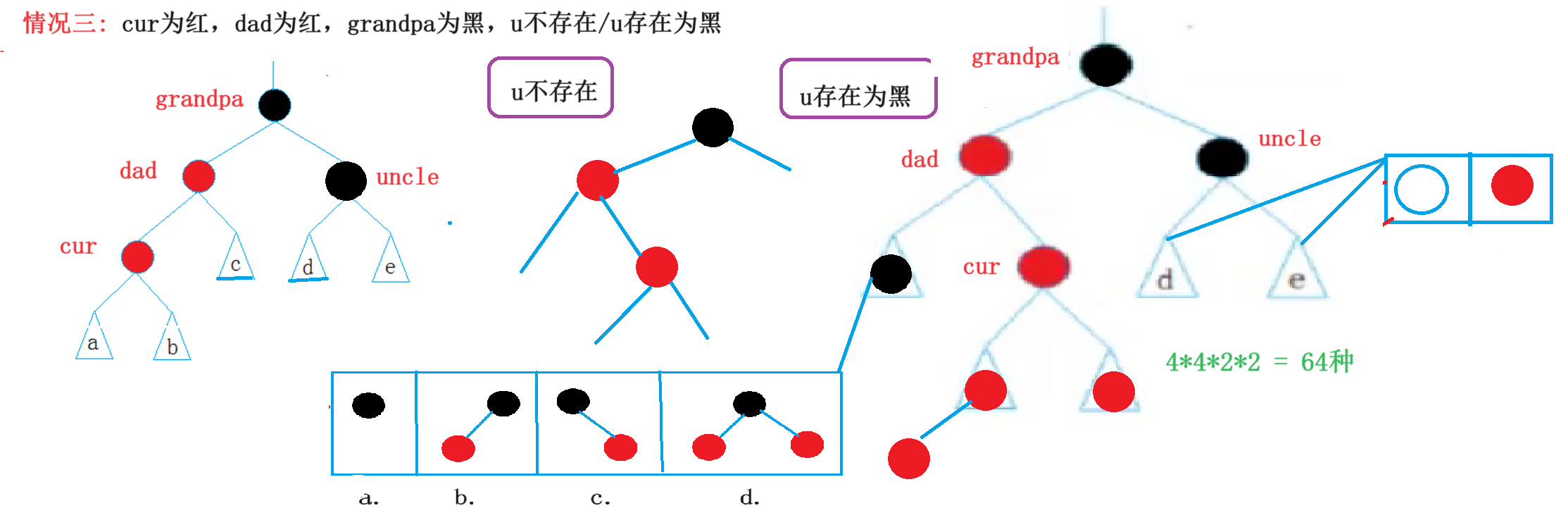
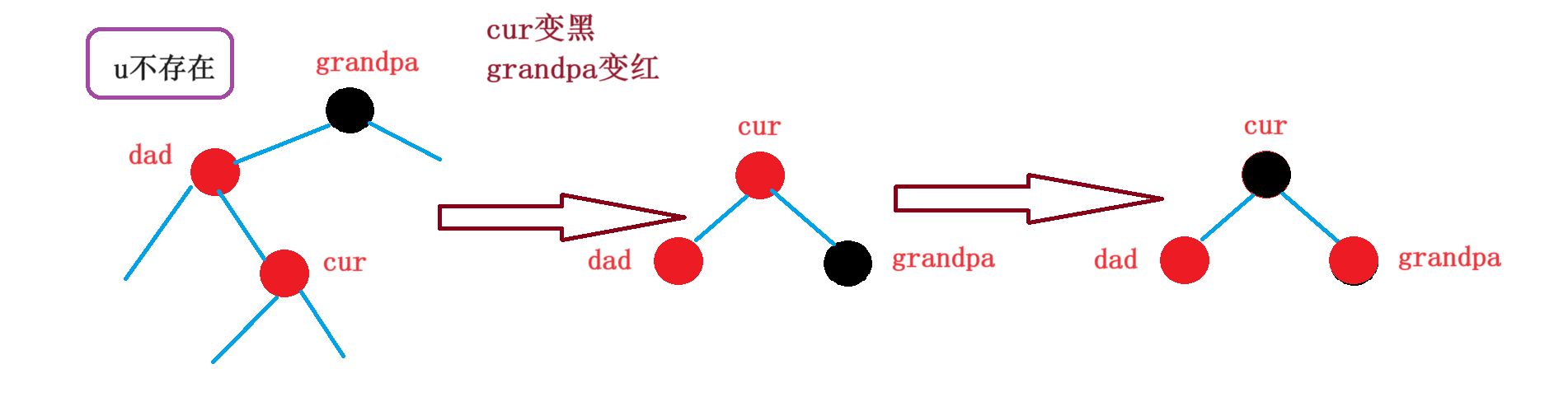
在这里插入图片描述

1.uncle不存在

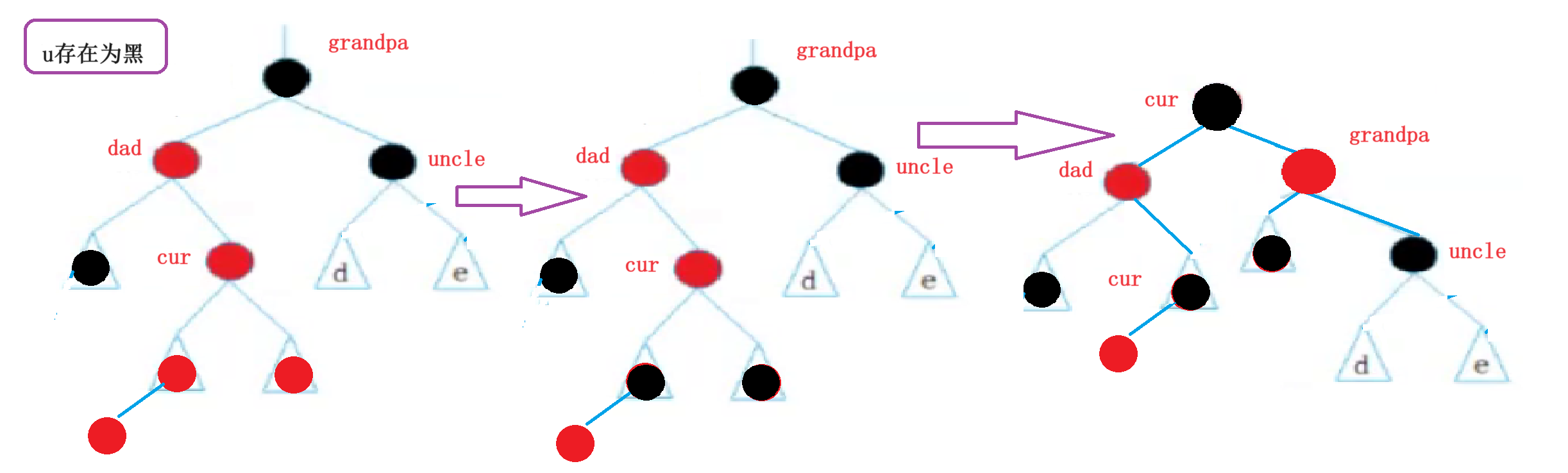
在这里插入图片描述

2.uncle存在为黑

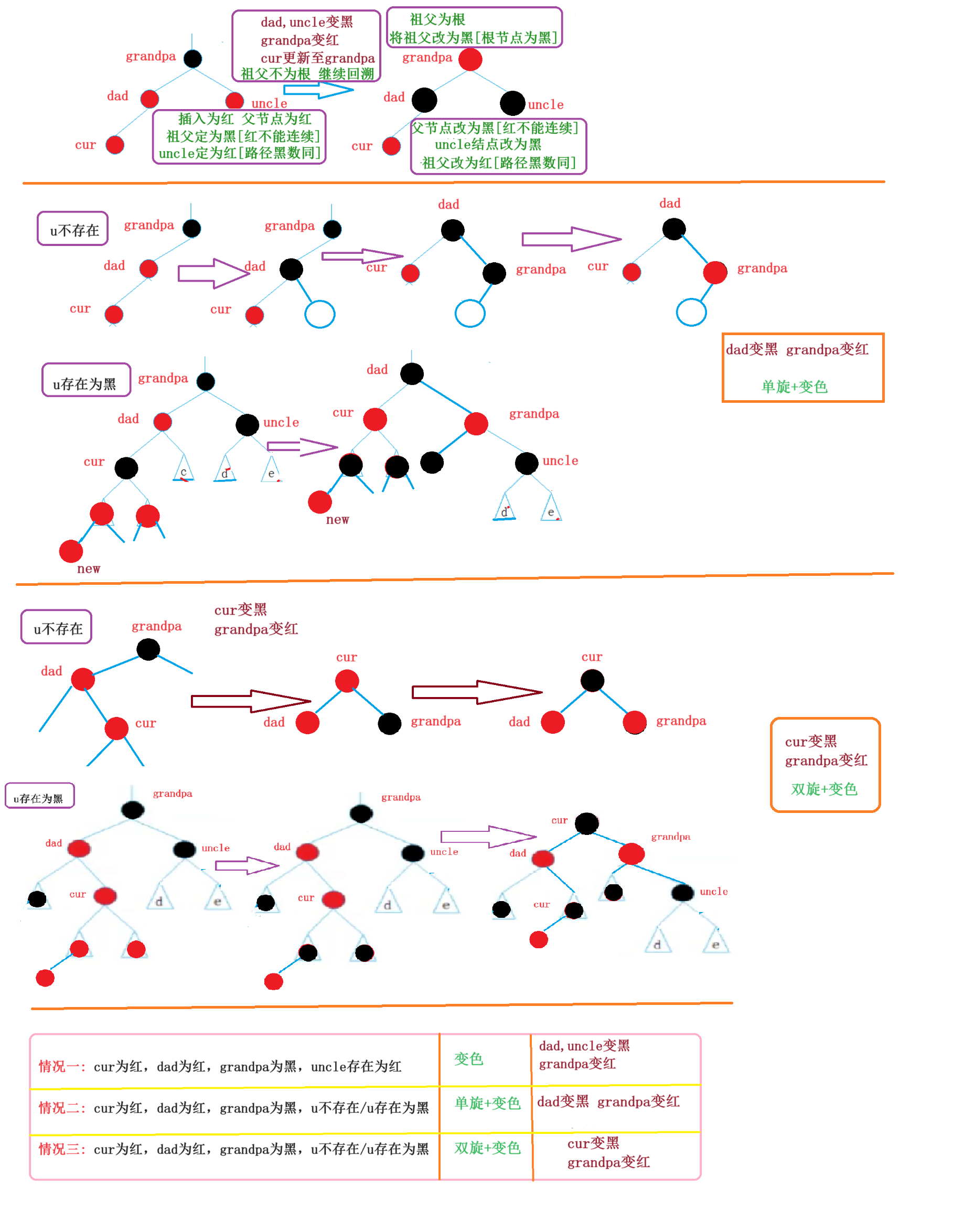
在这里插入图片描述

3.4总结

在这里插入图片描述
在这里插入图片描述

4.看图写代码[有手就行]

4.1RedBlackTree.h

#pragma once
#define _CRT_SECURE_NO_WARNINGS 
#include <iostream>
#include <list>
#include <vector>
#include <algorithm>
#include <array>
#include <time.h>
#include <queue>
#include <stack>
#include <string>
#include <set>
#include <map>
#include <functional>
#include <assert.h>
using namespace std;

//颜色枚举
enum Colour
{
	RED,
	BLACK
};

//结点类
template<class K, class V>
struct RBTreeNode
{
	RBTreeNode<K, V>* _left;
	RBTreeNode<K, V>* _right;
	RBTreeNode<K, V>* _parent;

	pair<K, V> _kv;
	Colour _col;

	RBTreeNode(const pair<K, V>& kv)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _kv(kv)
	{
	
	}
};

//RBTree类
template<class K, class V>
struct RBTree
{
	typedef RBTreeNode<K, V> Node;
public:
	
	//插入创建红黑树
	bool Insert(const pair<K, V>& kv)
	{
///二叉搜索树插入///
		//根节点为空
		if (_root == nullptr)
		{
			_root = new Node(kv);
			_root->_col = BLACK;  //根节点颜色为黑
			return true;
		}

		//不为空 定位至合适位置
		Node* dad = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < kv.first)
			{
				dad = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first)
			{
				dad = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}

		//父连接子
		cur = new Node(kv);
		cur->_col = RED;
		if (dad->_kv.first < kv.first)
		{
			dad->_right = cur;
		}
		else
		{
			dad->_left = cur;
		}
		//子继承父
		cur->_parent = dad;
构建红黑树	

    //cur[红]此时定位新插入位置 若父为红
	while (dad && dad->_col == RED)
	{
		//dad && dad->_col == RED
		//二次循环来到此处 
		// 1.父为空 则cur为根 [最后控制cur变黑] 循环结束
		// 2.父为黑 无需操作
		Node* grandpa = dad->_parent;

		//若父为红 祖父定存在且为黑
		assert(grandpa);
		assert(grandpa->_col == BLACK);

        /判断uncle位置///

		//父为左子树 uncle为右子树
		if (dad == grandpa->_left)
		{
			Node* uncle = grandpa->_right;

			//情况一、uncle存在为红 变色+回溯
			//dad-uncle变黑 grandpa变红
			if (uncle && uncle->_col == RED)
			{
				//变色
				dad->_col = uncle->_col = BLACK;
				grandpa->_col = RED;
				//回溯
				cur = grandpa;
				dad = cur->_parent;
			}

			//情况二-三：uncle不存在 存在且为黑
			else
			{
				
				if (cur == dad->_left)
				{
					//情况二：右单旋+变色
					RotateR(grandpa);
					dad->_col = BLACK;
					grandpa->_col = RED;
				}
				else
				{
					//情况三：左右双旋+变色
					RotateL(dad);
					RotateR(grandpa);
					cur->_col = BLACK;
					grandpa->_col = RED;
				}

				break;
			}
		}
		//父为右子树 uncle为左子树
		else 
		{
			Node* uncle = grandpa->_left;
			//情况一
			if (uncle && uncle->_col == RED)
			{
				//变色
				dad->_col = uncle->_col = BLACK;
				grandpa->_col = RED;
				//回溯
				cur = grandpa;
				dad = cur->_parent;
			}
			else
			{
				if (cur == dad->_right)
				{
					//情况二：左单旋+变色
					RotateL(grandpa);
					dad->_col = BLACK;
					grandpa->_col = RED;
				}
				else
				{
					//情况三：右左单旋+变色
					RotateR(dad);
					RotateL(grandpa);
					cur->_col = BLACK;
					grandpa->_col = RED;
				}

				break;
			}
		}

	}

	_root->_col = BLACK;
	return true;
}
    
    //中序遍历
    void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}

	//判断是否是红黑树
    bool IsRBTree()
	{
		///空树默认为真
		if (_root == nullptr)
		{
			return true;
		}

		//根节点颜色
		if (_root->_col == RED)
		{
			cout << "根结点颜色错误!" << endl;
			return false;
		}

		//某一条路径黑色结点数量
		int certain = 0;

		return PrevJudge(_root, 0, certain);
	}

private:

    //BNcount: black node count
	bool PrevJudge(Node* root, int BNcount, int& certain)
	{
		//遇空 -- 当前路径结束
		if (root == nullptr)
		{
			//指向此if时 某一条路径已结束 且 为第一条路径[第一次传参]
			if (certain == 0)
			{
				certain = BNcount;
				return true;
			}

			//判断性质4
			if (BNcount != certain)
			{
				cout << "性质4违例:存在某一路径黑色节点的数量不等!" << endl;
				return false;
			}
			else
			{
				return true;
			}
		}

		//遇黑--值++
		if (root->_col == BLACK)
		{
			++BNcount;
		}

		//遇红--连坐判断
		if (root->_col == RED && root->_parent->_col == RED)
		{
			cout << "性质3违例: 存在连续红节点!" << endl;
			return false;
		}

		return PrevJudge(root->_left, BNcount, certain)
			&& PrevJudge(root->_right, BNcount, certain);
	}

	//中序遍历
	void _InOrder(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}

		_InOrder(root->_left);
		cout << root->_kv.first << ":" << root->_kv.second << endl;
		_InOrder(root->_right);
	}

	//左单旋
	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if (subRL)
			subRL->_parent = parent;

		Node* grandpa = parent->_parent;

		subR->_left = parent;
		parent->_parent = subR;

		if (_root == parent)
		{
			_root = subR;
			subR->_parent = nullptr;
		}
		else
		{
			if (grandpa->_left == parent)
			{
				grandpa->_left = subR;
			}
			else
			{
				grandpa->_right = subR;
			}

			subR->_parent = grandpa;
		}

	}

	//右单旋
	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		parent->_left = subLR;
		if (subLR)
		{
			subLR->_parent = parent;
		}

		Node* grandpa = parent->_parent;

		subL->_right = parent;
		parent->_parent = subL;

		if (_root == parent)
		{
			_root = subL;
			subL->_parent = nullptr;
		}
		else
		{
			if (grandpa->_left == parent)
			{
				grandpa->_left = subL;
			}
			else
			{
				grandpa->_right = subL;
			}

			subL->_parent = grandpa;
		}

	}

private:
	Node* _root = nullptr;
};

void TestRBTree1()
{
	int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
	int b[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
	int c[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14, 0, 5, 30, 25, 20, 4, 13, 30, 28,27 };
	RBTree<int, int> tree;
	for (auto e : c)
	{
		tree.Insert(make_pair(e, e));
	}

	cout << "此树中序遍历" << endl;
	tree.InOrder();

	if (tree.IsRBTree())
	{
		cout << "此树为红黑树!" << endl;
	}
	else
	{
		cout << "此树不是红黑树!" << endl;
	}
}

void TestRBTree2()
{
	srand(time(0));
	size_t N = 10;
	RBTree<int, int> tree;
	for (size_t i = 0; i < N; ++i)
	{
		int x = rand();
		cout << "Insert:" << x << ":" << i << endl;
		tree.Insert(make_pair(x, i));
	}

	if (tree.IsRBTree())
	{
		cout << "此树为红黑树!" << endl;
	}
	else
	{
		cout << "此树不是红黑树!" << endl;
	}
}

4.2Test.cpp

#define _CRT_SECURE_NO_WARNINGS 
#include <iostream>
#include <list>
#include <vector>
#include <algorithm>
#include <array>
#include <time.h>
#include <queue>
#include <stack>
#include <string>
#include <set>
#include <map>
#include <functional>
using namespace std;

#include "RedBlackTree.h"

int main()
{
	TestRBTree2();
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1052578.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

FOC控制算法

FOC控制算法

目录 一、FOC介绍 二、FOC基本概念 1、为什么是三相&#xff1f; 2、FOC矢量控制总体算法简述 3、为什么FOC不一定需要电流采样&#xff1f;参考链接 4、FOC的分类 &#xff08;1&#xff09;有感FOC与无感FOC 三、FOC中电流采样 参考链接 1、高端采样 2、低端采样 …
阅读更多...
ChatGPT 学习笔记 | 什么是 Prompt-tuning？

ChatGPT 学习笔记 | 什么是 Prompt-tuning？

文章目录 一、前言二、主要内容三、总结 &#x1f349; CSDN 叶庭云&#xff1a;https://yetingyun.blog.csdn.net/ 一、前言 Prompt-tuning is an efficient, low-cost way of adapting an AI foundation model to new downstream tasks without retraining the model and upd…
阅读更多...
redo日志（下）

redo日志（下）

title: “redo日志&#xff08;下&#xff09;” createTime: 2022-03-06T15:52:4108:00 updateTime: 2022-03-06T15:52:4108:00 draft: false author: “ggball” tags: [“mysql”] categories: [“db”] description: “” redo log的刷盘时机 log buffer 空间不足时&…
阅读更多...
No167.精选前端面试题，享受每天的挑战和学习

No167.精选前端面试题，享受每天的挑战和学习

🤍 前端开发工程师（主业）、技术博主（副业）、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云课上架的前后端实战课程《Vue.js 和 Egg.js 开发企业级健康管理项目》、《带你从入…
阅读更多...
通用返回结果类ResultVO

通用返回结果类ResultVO

1. 定义通用返回结果类 ​ 定义ResultVO类&#xff0c;作返回给前端的对象结构&#xff0c;主要有4个字段 code : 错误码 data : 内容message : 消息description : 具体描述 import lombok.Data; import java.io.Serializable;/*** 通用返回结果类* param <T>*/ Data …
阅读更多...
ABAP Web dynpro layout动态可见

ABAP Web dynpro layout动态可见

ABAP Web dynpro layout动态可见 新增的元素设置不可见 在视图初始化方法中下&#xff0c;获取选中数据&#xff0c;当选中数据不在配置表中&#xff0c;对该视图中容器的子元素显示出来 效果图&#xff1a; 完整代码&#xff1a; DATA lo_nd_nod_pay_info TYPE REF TO if_…
阅读更多...
Cocos Creator3.8 实战问题（一）cocos creator prefab 无法显示内容

Cocos Creator3.8 实战问题（一）cocos creator prefab 无法显示内容

问题描述&#xff1a; cocos creator prefab 无法显示内容&#xff0c; 或者只显示一部分内容。 creator编辑器中能看见&#xff1a; 预览时&#xff0c;看不见内容&#xff1a; **问题原因&#xff1a;** prefab node 所在的layer&#xff0c;默认是default。 解决方法&…
阅读更多...
CentOS上网卡不显示的问题

CentOS上网卡不显示的问题

文章目录 1.问题描述 1.问题描述 ifconfig下看不到ens33网卡了。systemctl status network #查看网卡状态报下面的问题网上说的解决方式有以下三种&#xff1a; 第一种&#xff1a; 和 NetworkManager 服务有冲突&#xff0c;这个好解决&#xff0c;直接关闭 NetworkManger 服…
阅读更多...
简单三步 用GPT-4和Gamma自动生成PPT PDF

简单三步 用GPT-4和Gamma自动生成PPT PDF

1. 用GPT-4 生产PPT内容 我想把下面的文章做成PPT&#xff0c;请你给出详细的大纲和内容 用于谋生的知识&#xff0c;学生主要工作是学习&#xff0c;成年人的工作是养家糊口&#xff0c;这是基本的要求&#xff0c;在这之上&#xff0c;才能有更高的追求。 不要短期期望过高…
阅读更多...
26940-2011 牡蛎干 思维导图

26940-2011 牡蛎干 思维导图

声明 本文是学习GB-T 26940-2011 牡蛎干. 而整理的学习笔记,分享出来希望更多人受益,如果存在侵权请及时联系我们 1 范围 本标准规定了牡蛎干的要求、试验方法、检验规则、标签、包装、贮存和运输要求。 本标准适用于养殖或野生牡蛎(Ostrea spp.)为原料&#xff0c;经取肉、…
阅读更多...
9.30国庆作业1

9.30国庆作业1

消息队列实现进程之间通信方式代码&#xff0c;现象 接收消息 #include<myhead.h>//消息结构体 typedef struct {long msgtype; //消息类型char data[1024]; //消息正文 }Msg_ds;#define SIZE sizeof(Msg_ds)-sizeof(long) //正文大小int main(int a…
阅读更多...
小谈设计模式（7）—装饰模式

小谈设计模式（7）—装饰模式

小谈设计模式&#xff08;7&#xff09;—装饰模式 专栏介绍专栏地址专栏介绍 装饰模式装饰模式角色Component&#xff08;抽象组件&#xff09;ConcreteComponent&#xff08;具体组件&#xff09;Decorator&#xff08;抽象装饰器&#xff09;ConcreteDecorator&#xff08;具…
阅读更多...
数据集划分——train_test_split函数使用说明

数据集划分——train_test_split函数使用说明

当我们拿到数据集时&#xff0c;首先需要对数据集进行划分训练集和测试集&#xff0c;sklearn提供了相应的函数供我们使用 一、讲解 快速随机划分数据集&#xff0c;可自定义比例进行划分训练集和测试集 二、官网API 官网API sklearn.model_selection.train_test_split(*a…
阅读更多...
ubuntu安装PhotoPrism，并开启安卓照片同步

ubuntu安装PhotoPrism，并开启安卓照片同步

之前安装了黑群晖7.2&#xff0c;并开启了Photo&#xff0c;照片同步用的挺好。唯一的缺陷是群晖的照片搜索太弱鸡了&#xff0c;基本上关键字搜索是一点不可用&#xff0c;常见的“花”&#xff0c;“山”&#xff0c;“文件”&#xff0c;“证件”都是不可用的。 后来了解到了…
阅读更多...
NLP 02 RNN

NLP 02 RNN

一、RNN RNN(Recurrent Neural Network),中文称作循环神经网络它一般以序列数据为输入通过网络内部的结构设计有效捕捉序列之间的关系特征,一般也是以序列形式进行输出。 传统神经网络(包括CNN)&#xff0c;输入和输出都是互相独立的。但有些任务&#xff0c;后续的输出和之前…
阅读更多...
《Operating Systems: Three Easy Pieces》 操作系统【一】 虚拟化 CPU

《Operating Systems: Three Easy Pieces》 操作系统【一】 虚拟化 CPU

&#xff08;一&#xff09;操作系统介绍 1.虚拟化 CPU 书上代码 &#xff1a; #include <stdio.h> #include <stdlib.h> #include <sys/time.h> #include <assert.h> #include "common.h"int main(int argc, char *argv[]) {if (argc ! …
阅读更多...
TensorFlow学习1：使用官方模型进行图片分类

TensorFlow学习1：使用官方模型进行图片分类

前言 人工智能以后会越来越发达&#xff0c;趁着现在简单学习一下。机器学习框架有很多&#xff0c;这里觉得学习谷歌的 TensorFlow&#xff0c;谷歌的技术还是很有保证的&#xff0c;另外TensorFlow 的中文文档真的很友好。 文档&#xff1a; https://tensorflow.google.cn/…
阅读更多...
使用 gst-element-maker 创建一个完全透传的 videofilter 插件

使用 gst-element-maker 创建一个完全透传的 videofilter 插件

系列文章目录 创建 gstreamer 插件的几种方式 使用 gst-template 创建自己的 gstreamer 插件 使用 gst-plugins-bad 里面的 gst-element-maker 工具创建gstreamer 插件 使用 gst-element-maker 创建一个完全透传的 videofilter 插件 文章目录 系列文章目录前言一、使用gst-ele…
阅读更多...
亿图脑图新版本支持思维导图一键生成PPT、音视频等格式，办公提效再升级

亿图脑图新版本支持思维导图一键生成PPT、音视频等格式，办公提效再升级

近日&#xff0c;国产思维导图软件——亿图脑图MindMaster发布了全新版本V10.9.0&#xff0c;本次亿图脑图的升级给用户带来了极大的惊喜。全新升级的亿图脑图MindMaster不仅支持20格式的文件智能解析成思维导图&#xff0c;还支持思维导图一键生成PPT、音频、视频等内容形式&a…
阅读更多...
公认黑客守则

公认黑客守则

1、不要恶意的破坏任何系统&#xff0c;恶意的破坏他人的软件或服务器将要承担法律责任&#xff0c;如果你只是使用计算机&#xff0c;也是非法的&#xff0c;千万不要破坏别人的文件或数据 2、不要修改别人的任何系统文件&#xff0c;如果你是为了进入而修改它&#xff0c;请在…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023