给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
- 首先找到需要删除的节点;
- 如果找到了,删除它。
示例 1:
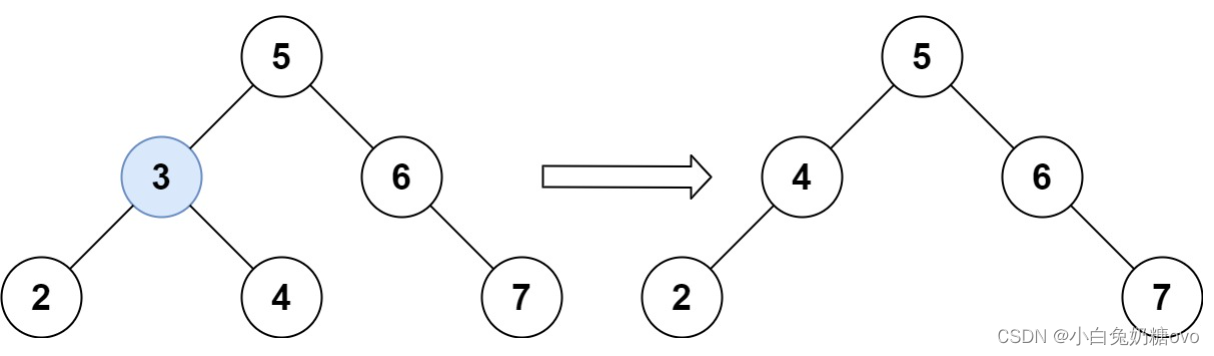
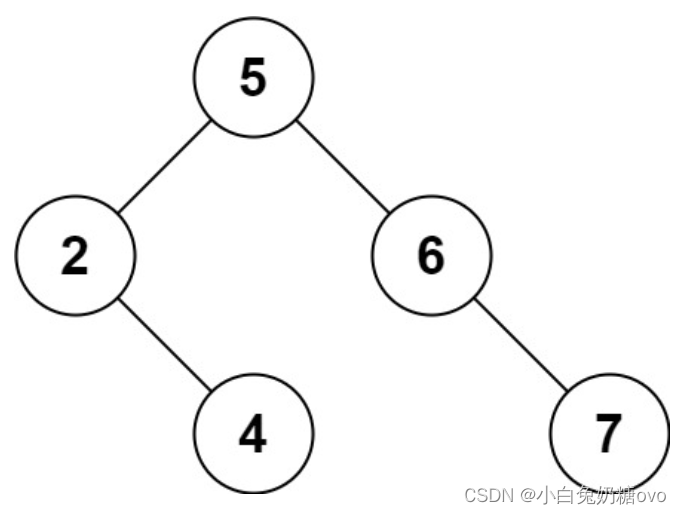
输入:root = [5,3,6,2,4,null,7], key = 3
输出:[5,4,6,2,null,null,7]
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
- 一个正确的答案是
[5,4,6,2,null,null,7], 如下图所示。 - 另一个正确答案是
[5,2,6,null,4,null,7]。
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
示例 3:
输入: root = [], key = 0
输出: []
提示:
节点数的范围 [0, 104].
- 105 <= Node.val <= 105
节点值唯一
root 是合法的二叉搜索树
- 105 <= key <= 105
进阶: 要求算法时间复杂度为 O(h),h 为树的高度。
AC:
/*
* @lc app=leetcode.cn id=450 lang=cpp
*
* [450] 删除二叉搜索树中的节点
*/
// @lc code=start
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if(!root)
return root;
if(root->val == key)
{
if(!root->left && !root->right)
{
delete root;
return NULL;
}
else if(root->left && !root->right)
{
auto retNode = root->left;
delete root;
return retNode;
}
else if(!root->left && root->right)
{
auto retNode = root->right;
delete root;
return retNode;
}
else {
TreeNode* cur = root->right;
while(cur->left)
{
cur = cur->left;
}
cur->left = root->left;
TreeNode* tmp = root;
root = root->right;
delete tmp;
return root;
}
}
if(root->val < key)
root->right = deleteNode(root->right, key);
if(root->val > key)
root->left = deleteNode(root->left, key);
return root;
}
};
// @lc code=end

下面给出一种普通二叉树删除节点的做法:
/*
* @lc app=leetcode.cn id=450 lang=cpp
*
* [450] 删除二叉树中的节点
*/
// @lc code=start
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if(root == NULL)
return root;
if(root->val == key)
{
if(root->right == NULL)
return root->left;
TreeNode* cur = root->right;
while(cur->left)
{
cur = cur->left;
}
swap(cur->val, root->val);
}
root->left = deleteNode(root->left, key);
root->right = deleteNode(root->right, key);
return root;
}
};
// @lc code=end
这段代码可以处理三种情况,即:
- 待删除节点的左右孩子均为空。
- 待删除节点的左右孩子有一个为空。
- 待删除节点的左右孩子均不为空。
对于第一种情况,代码中的 if(root->right == NULL) 判断了待删除节点的右孩子是否为空。如果右孩子为空,那么待删除节点的左孩子就成为了删除后的根节点,因此直接返回左孩子即可。
对于第二种情况,代码中的 root->left = deleteNode(root->left, key) 和 root->right = deleteNode(root->right, key) 分别递归处理了待删除节点的左孩子和右孩子。如果其中一个孩子为空,那么递归函数会返回另一个孩子,从而将其作为删除后的根节点的孩子。
对于第三种情况,代码中的 swap(cur->val, root->val) 将待删除节点的值替换为其右子树中最小节点的值,然后递归删除右子树中的最小节点。这样可以保证删除后的树仍然是一棵二叉搜索树。
The code above is a block of code that appears in a function for deleting a node from a binary search tree. The function takes a pointer to the root node of the binary search tree and a value to be deleted as input, and returns a pointer to the root node of the modified binary search tree.
The code first checks if the root node is null. If the root node is null, then the function returns null, indicating that the binary search tree is empty.
If the value to be deleted is equal to the value of the root node, then the code checks if the root node has a right child. If the root node does not have a right child, then the code returns the left child of the root node, effectively deleting the root node from the binary search tree. If the root node has a right child, then the code finds the leftmost node in the right subtree of the root node, swaps its value with the value of the root node, and then deletes the leftmost node from the right subtree.
If the value to be deleted is less than the value of the root node, then the code recursively calls the deleteNode function on the left child of the root node. If the value to be deleted is greater than the value of the root node, then the code recursively calls the deleteNode function on the right child of the root node.
Overall, this block of code is a simple and efficient way to delete a node from a binary search tree. The code uses a recursive approach to traverse the binary search tree and find the node to be deleted. Once the node is found, the code handles three different cases depending on whether the node has zero, one, or two children. One possible way to improve the code would be to add error checking to ensure that the root node is not null before accessing its value. Additionally, the variable names could be more descriptive to make the code easier to read and understand.