1.归并树的性质

• 每个初始归并段对应一个叶子结点，把归并段的块数作为叶子的权值
• 归并树的WPL=树中所有叶结点的带权路径长度之和
• 归并过程中的磁盘I/O次数=归并树的WPL*2

如下图：

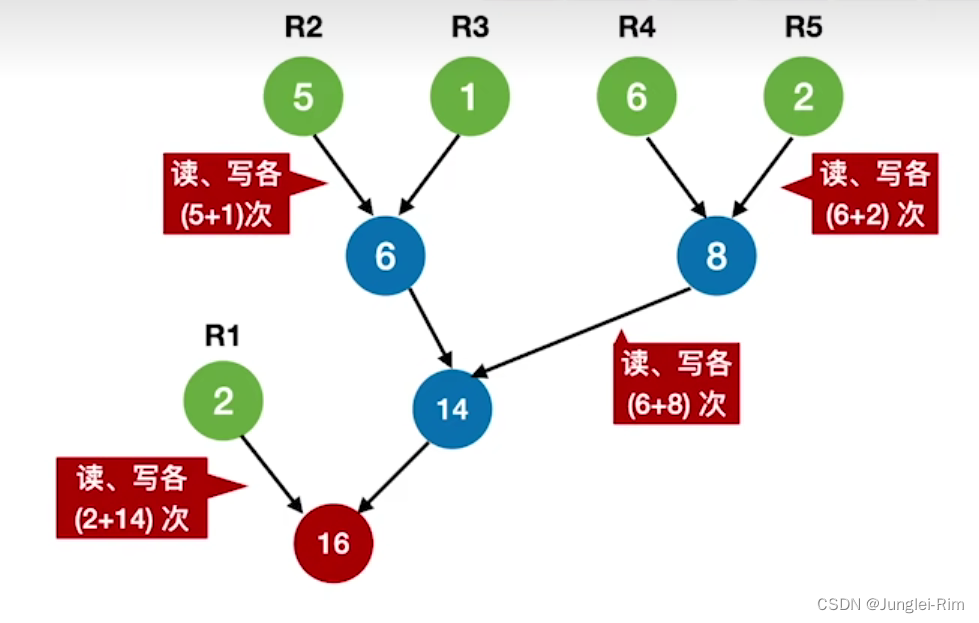
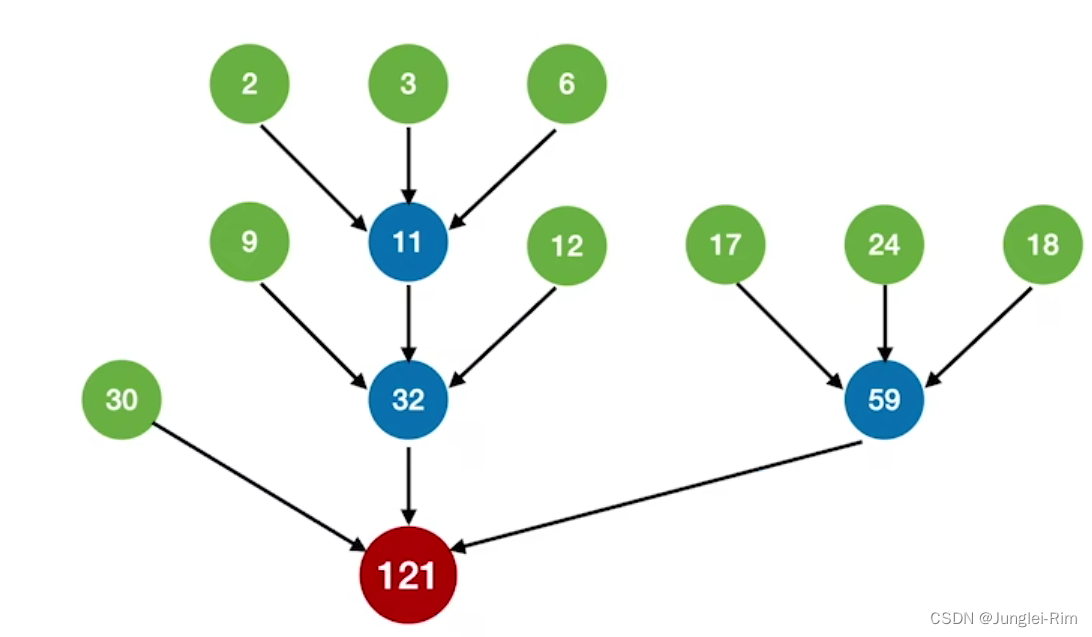
每个初始归并段看作一个叶子结点，归并段的长度作为结点权值，
则上面这棵归并树的带权路径长度WPL= 2*1+(5+1+6+2)*3= 44 =读磁盘的次数=写磁盘的次数。

重要结论:归并过程中的磁盘I/O次数=归并树的WPL*2。

要让磁盘I/O次数最少,就要使归并树WPL最小：哈夫曼树。

2.构造2路归并的最佳归并树

构造k叉哈夫曼树：
每次选择k个根节点权值最小的树合并，
并将k个根节点的权值之和作为新的根节点的权值。

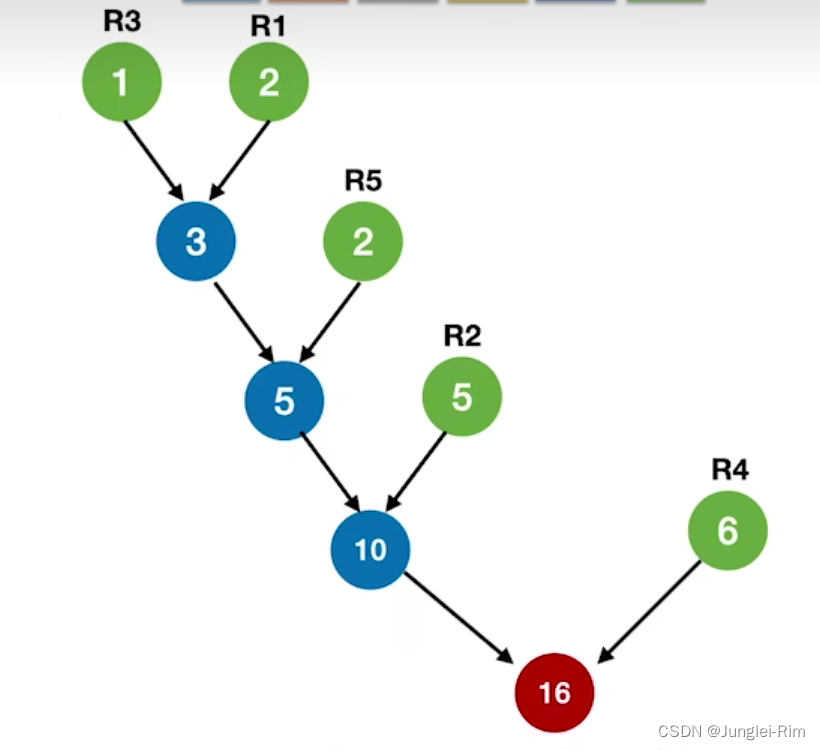
3.多路归并的情况

1.归并段数量能构成严格k叉归并树

2.归并段数量不足时

注意︰对于k叉归并，若初始归并段的数量无法构成严格的k叉归并树，
则需要补充几个长度为0的“虚段”，再进行k叉哈夫曼树的构造。
如下图：

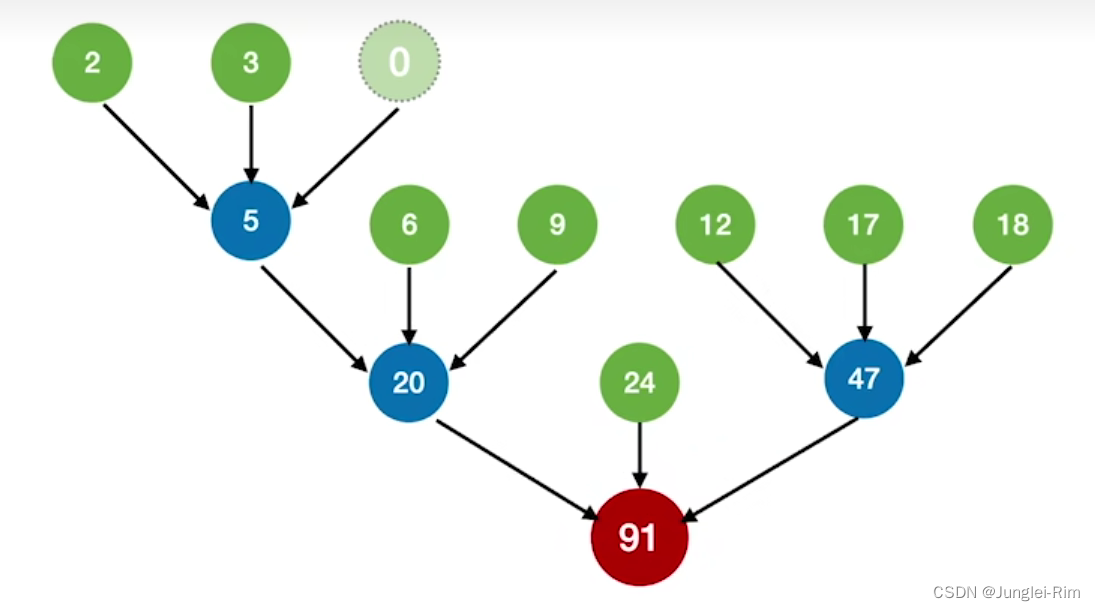
3.添加虚段的数量

k叉的最佳归并树一定是一棵严格的k叉树，即树中只包含度为k、度为0的结点。

设度为k的结点有nk 个，度为0的结点有no个，归并树总结点数=n则:

初始归并段数量+虚段数量=n0
$n=n0+nk$
$k\ast nk=n-1$
$n0=(k-1)nk+1$
$nk=\frac{n0-1}{k-1}$(如果是“严格k叉树”,一定能除得尽)

• ①若（初始归并段数量-1) %(k-1) = 0，说明刚好可以构成严格k叉树，此时不需要添加虚段
• ②若（初始归并段数量-1) %(k-1) = u≠0，则需要补充(k-1)- u个虚段