【C++数据结构】二叉树搜索树【完整版】

news2024/12/26 10:36:09

目录

一、二叉搜索树的定义

 二、二叉搜索树的实现：

1、树节点的创建--BSTreeNode

 2、二叉搜索树的基本框架--BSTree

3、插入节点--Insert

 4、中序遍历--InOrder

5、 查找--Find

6、 删除--erase

完整代码：

三、二叉搜索树的应用

1、key的模型 ：判断在不在

2、key/value的模型：通过key找value 

key/value的应用场景

应用场景1--中英文互译

应用场景2--统计水果出现次数

 四、二叉搜索树性能分析

一、二叉搜索树的定义

二叉搜索树（也称为搜索二叉树）又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

  • 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
  • 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
  • 它的左右子树也分别为二叉搜索树

 二、二叉搜索树的实现：

这里最好不用递归，递归比非递归更复杂，故用非递归实现

分两个文件：

BSTree.hpp(因为要用模板实现，而模板的实现和声明要放在一起的，若用模板实现就可用.hpp为后缀和 Test.c

1、树节点的创建--BSTreeNode

 树是由节点组成的，故应写个BSTreeNode用来表示每个树节点，_left表示左指针，_right表示右指针，还有一个位置用来存值_key，因为无法确定存的是什么类型的值，故用模板来实现通用，设置成struct是因为树的节点对外是公开的，外部都可以访问的

template<class K>
struct BSTreeNode
{
	BSTreeNode(const K& key)
		:_key(key)
		, _left(nullptr)
		, _right(nullptr)
	{}

	BSTreeNode<K>* _left;
	BSTreeNode<K>* _right;
	K _key;
};

 2、二叉搜索树的基本框架--BSTree

对于树的成员变量，一个根节点即可

template<class K>
class BSTree //Binary Search Tree
{
	typedef BSTreeNode<K> Node;
public:

private:
	Node* _root = nullptr;可以直接定义,就一个成员变量，无需写个构造函数
};

3、插入节点--Insert

 这个函数需要有返回值的，以bool作为返回类型，因为这棵树中不允许数据冗余，即不能出现相同的数据。

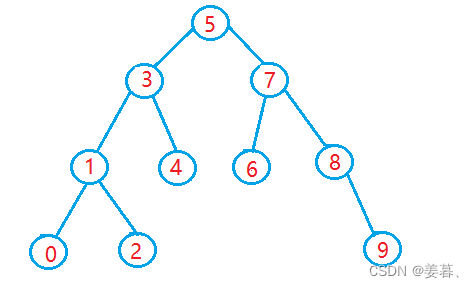
插入就是用性质：左子树的值都比当前根节点的值小，右子树的值都比当前根节点的值大

若插入一个数据key，从根节点（用cur指针来表示当前位置）开始往下比就好了

①、如果key比当前节点的值大，那就接着往右走

②、如果key比当前节点的值小，那就接着往左走

对于①②直到找到一个空位置插入即可

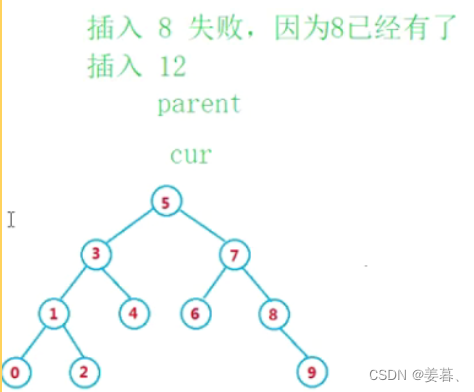
③、如果走的过程中遇到相等的值，说明该key值不能插入，但要注意一个条件，如果这棵树本来就为空，那就直接把数据插入到根节点中就好

链接问题：

插入一个节点，必然要与树链接，若不链接，这个节点就是个临时数据，出了作用域就没了，但若把他链接到树上就能正常访问了，故这里采用双指针法，cur表示当前节点，再定义一个parent，每次cur走之前，先把cur赋值给parent，这样最后cur走到空了，parent能记录到cur的上一位置，而这上一位置就是要找的cur要与其链接的位置，至于cur插入到parent的左还是右，若值比parent的值大，则插到右边，小，则插到左边

bool Insert(const K& key)
{
	if (_root == nullptr)
	{//若为空树，就给它一个节点
		_root = new Node(key);//new是开空间+初始化，所以要调用构造函数，你要写的
		return true;
	}
	Node* cur = _root;//从根节点开始比较
	Node* parent = nullptr;
	while (cur)
	{
		//都会找一个空位置插入，不会说挪动节点来进行插入
		if (cur->_key > key)
		{
			parent = cur;
			cur = cur->_left;

		}
		else if (cur->_key < key)
		{
			parent = cur;
			cur = cur->_right;
		}
		else
		{//若在走的过程中遇到相同的数据，返回假，这个数据无法插入
			return false;
		}
	}
	cur = new Node(key);//向这个空位置插入数据
	//利用parent的位置与cur连接
	if (parent->_key > key)
		parent->_left = cur;//比根节点小，链接到左边
	else
		parent->_right = cur;//比根节点大，链接到右边
	return true;
}

 4、中序遍历--InOrder

  这里用两个成员函数实现，为什么？中序遍历你要传树的根节点，而根节点就是类的私有成员变量，而你的中序遍历一定是在类外使用的，无法直接访问_root

解决方法：

法一、写个成员函数获得一下_root是可以的

法二、用两个成员函数，即用InOrder来传这个_root，成员函数访问你_root一定是没问题的，那么_InOrder直接用来中序遍历即可，调用时直接调用InOrder即可

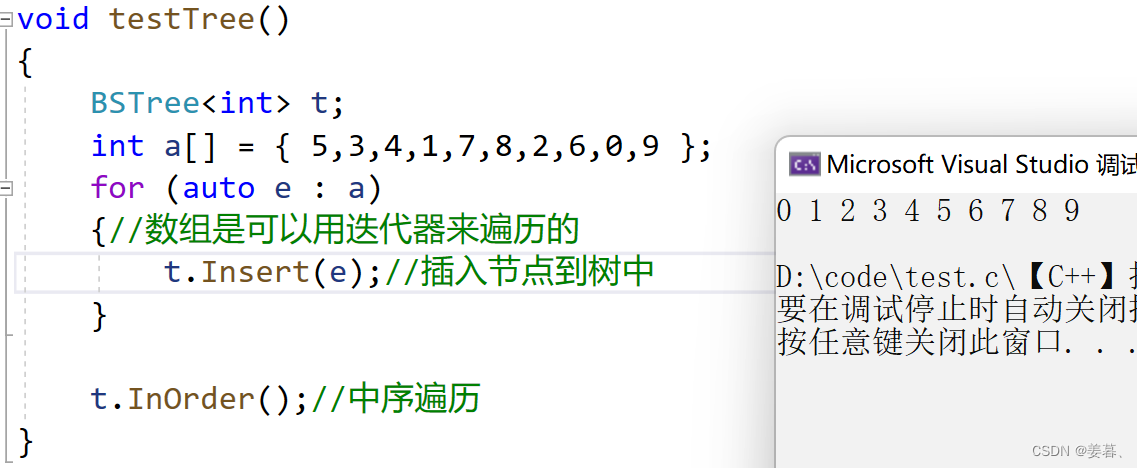
void InOrder()
{
	_InOrder(_root);
	cout << endl;
}
//下面的可以放到private里面
void _InOrder(Node* root)
{
	if (root == nullptr)
		return;

	_InOrder(root->_left);
	cout << root->_key << " ";
	_InOrder(root->_right);
}

下面利用写的插入和中序遍历测试下代码：


void testTree()
{
	BSTree<int> t;
	int a[] = { 5,3,4,1,7,8,2,6,0,9 };
	for (auto e : a)
	{//数组是可以用迭代器来遍历的
		t.Insert(e);//插入节点到树中
	}

	t.InOrder();//中序遍历
}

 

5、 查找--Find

bool Find(const K& key)
{
	Node* cur = _root;
	while (cur)
	{
		if (cur->_key > key)	
		{
		cur = cur->_left;
		}
		else if (cur->_key < key)
		{
			cur = cur->_right;
		}
		else
		{
			return true;//说明相等，则找到了，返回真
		}
	}
	return false;//走到空还没找到，说明没有此数据
}

6、 删除--erase

1、观察现象：  

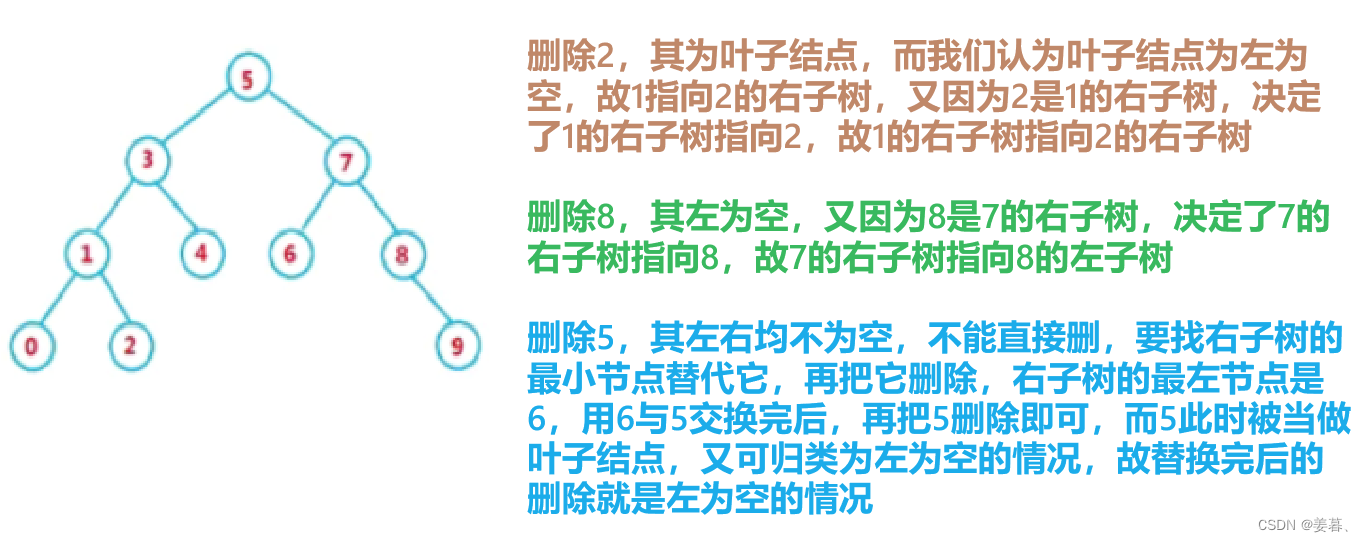
删除2，让父亲指向我的右，删除8，让父亲指向我的右，5不好删，因为他有两个孩子

左为空，父亲指向我的右，右为空，父亲指向我的左，叶子节点可以归纳为左为空（右为空也行，这里就假设用左为空），因为叶子的左右都为空，它父亲的指向他的左还是右均可

左为空，

2、细节考虑

A、待删除节点左为空或右为空的情况（叶子结点可归类为左为空）

删除一个节点是让其父亲（Parent）的左指针还是右指针指向cur？

【若cur的左子树为空】看cur到底是父亲的左子树还是右子树，若是父亲的左子树，则让父亲的左指向cur右子树 ，若为右子树，则让父亲的右指向cur的右子树

【若cur的右子树为空】若是父亲的左子树，则让父亲的左指向cur左子树 ，若为右子树，则让父亲的右指向cur的左子树

B、待删除节点左右都不为空的情况

节点的左右子树都不为空，不能直接删除，直接删除会导致二叉搜索树混乱，故用替代法删除。

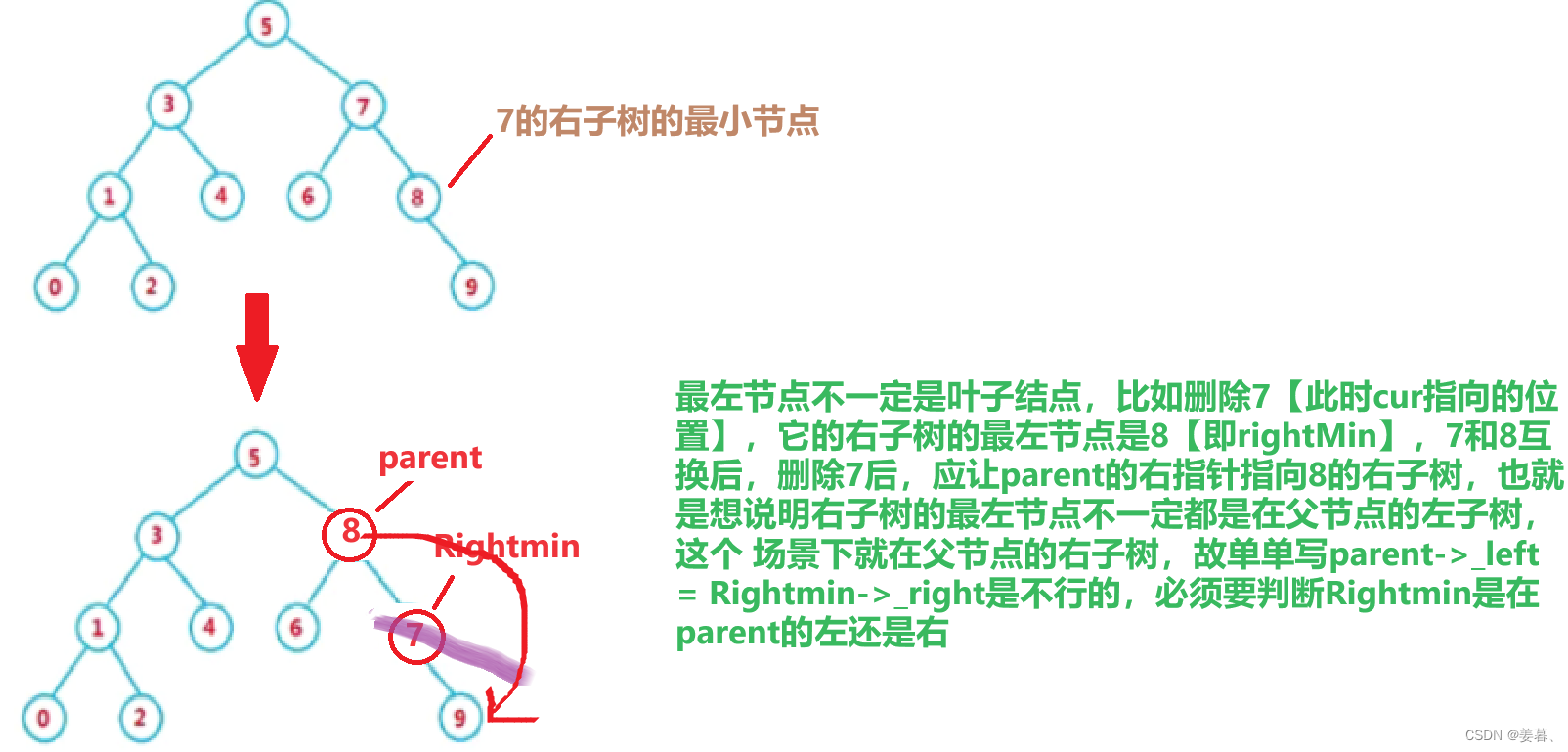
因为要符合左子树都比根节点小，右子树都比根节点大的性质，故要找左子树的最大节点或右子树的最小节点去替代它。（左子树最右边的节点是左子树最大节点，右子树的最左边的节点是右子树最小节点）【故假设我们下面就用右子树的最小节点】

比如删除7，可以用8（7的右子树的最左节点）来替代，那么替换完后，我删除这个7就可以直接删了，那么这个问题又转换到了被删除节点的左为空或者右为空，因为替换节点一定要么是最左边的节点要么是最右边的节点（不一定是叶子结点），那这个替换节点的左右子树一定存在左子树右子树有个为空的情况

所以删除 分三种情况

问题1：

删除一定要找到父亲，因为删完了还存在链接关系，所以单单用find去找是不行的，他找不到他的父亲节点，故还是用双指针法

 因为链接问题，所以删除关键看cur是在父亲的左还是右，而不是看cur的左边为空还是右边为空，这不符合所有场景

问题2：

最左节点不一定就是叶子结点，比如这里删除7，它的右子树的最左节点是8，则8替换完7后，8要被删除，他被删除完后，parent的右指针要指向rightMin的右节点

问题3：

parent初始值不能为nullptr，若删除7【che指针指向7】，因为要删除cur，Rightmin刚上来就=8，Rightmin的左子树为空，while循环都没进去，而parent它还是nullptr，那后续的链接肯定会有问题的，所以parent应该一上来就赋值为cur，而不是nullptr

问题4：

若要删除的节点是根节点，也要特别考虑，左为空，则让根=它的右节点，右为空，则让根=它的左节点

bool Erase(const K& key)
{
	Node* cur = _root;
	Node* parent = nullptr;
	while (cur)
	{
		if (cur->_key > key)
		{
			parent = cur;
			cur = cur->_left;
		}
		else if (cur->_key < key)
		{
			parent = cur;
			cur = cur->_right;
		}
		else
		{
			//找到了，开始删除
			//1.左为空
			if (cur->_left == nullptr)
			{
				if (cur == _root)
					_root = cur->_right;
				else
				{
					if (parent->_left == cur)
						parent->_left = cur->_right;//cur在父亲的左边，就让父亲的左指向cur的左
					else
						parent->_right = cur->_right;//cur在父亲的右边，就让父亲的右指向cur的右
				}
				delete cur;
			}
			//2.右为空
			else if (cur->_right == nullptr)
			{
				if (cur == _root)
					_root = cur->_left;
				else
				{
					if (parent->_right == cur)
						parent->_right = cur->_left;//cur在父亲的右边，就让父亲的右指向cur的左
					else
						parent->_left = cur->_left;//cur在父亲的左边，就让父亲的左指向cur的右
				}
				delete cur;
			}
			//3.左右都不为空
			else
			{//找左子树的最右节点或右子树的最小节点去替代
			 //这里用右子树的最小节点来替代
				Node* parent = cur;
				Node* Rightmin = cur->_right;//若用右树的最小节点，即右树最左节点
				while (Rightmin->_left)
				{//最左节点的左子树一定为空，故为判断条件
					parent = Rightmin;//替换节点不一定是叶子结点，故还要用parent来链接
					Rightmin = Rightmin->_left;
				}

				cur->_key = Rightmin->_key;//用cur的值来替代
				//转换成删除Rightmin
				//若它是parent的右子树，则父亲的右指向它的右
				//若它是parent的左子树，则父亲的左指向它的左
				if (Rightmin == parent->_left)
					parent->_left = Rightmin->_right;
				else
					parent->_right = Rightmin->_right;
				delete Rightmin;
			}
			return true;
		}
	}
	return false;//cur都为空了还没找到，则该数据不存在
}

完整代码：

BSTree.hpp

#pragma once
#include<iostream>
using namespace std;


template<class K>
struct BSTreeNode
{
	BSTreeNode(const K& key)
		:_key(key)
		, _left(nullptr)
		, _right(nullptr)
	{}

	BSTreeNode<K>* _left;
	BSTreeNode<K>* _right;
	K _key;

};
template<class K>
class BSTree //Binary Search Tree
{
	typedef BSTreeNode<K> Node;
public:
	bool Insert(const K& key)
	{
		if (_root == nullptr)
		{//若为空树，就给它一个节点
			_root = new Node(key);//new是开空间+初始化，所以要调用构造函数，你要写的
			return true;
		}
		Node* cur = _root;//从根节点开始比较
		Node* parent = nullptr;
		while (cur)
		{
			//都会找一个空位置插入，不会说挪动节点来进行插入
			if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;

			}
			else if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{//若在走的过程中遇到相同的数据，返回假，这个数据无法插入
				return false;
			}
		}
		cur = new Node(key);//向这个空位置插入数据
		//利用parent的位置与cur连接
		if (parent->_key > key)
			parent->_left = cur;//比根节点小，链接到左边
		else
			parent->_right = cur;//比根节点大，链接到右边
		return true;
	}

	bool Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key > key)	
			{
			cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				cur = cur->_right;
			}
			else
			{
				return true;//说明相等，则找到了，返回真
			}
		}
		return false;
	}

	bool Erase(const K& key)
	{
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				//找到了，开始删除
				//1.左为空
				if (cur->_left == nullptr)
				{
					if (cur == _root)
						_root = cur->_right;
					else
					{
						if (parent->_left == cur)
							parent->_left = cur->_right;//cur在父亲的左边，就让父亲的左指向cur的左
						else
							parent->_right = cur->_right;//cur在父亲的右边，就让父亲的右指向cur的右
					}
					delete cur;
				}
				//2.右为空
				else if (cur->_right == nullptr)
				{
					if (cur == _root)
						_root = cur->_left;
					else
					{
						if (parent->_right == cur)
							parent->_right = cur->_left;//cur在父亲的右边，就让父亲的右指向cur的左
						else
							parent->_left = cur->_left;//cur在父亲的左边，就让父亲的左指向cur的右
					}
					delete cur;
				}
				//3.左右都不为空
				else
				{//找左子树的最右节点或右子树的最小节点去替代
				 //这里用右子树的最小节点来替代
					Node* parent = cur;
					Node* Rightmin = cur->_right;//若用右树的最小节点，即右树最左节点
					while (Rightmin->_left)
					{//最左节点的左子树一定为空，故为判断条件
						parent = Rightmin;//替换节点不一定是叶子结点，故还要用parent来链接
						Rightmin = Rightmin->_left;
					}

					cur->_key = Rightmin->_key;//用cur的值来替代
					//转换成删除Rightmin
					//若它是parent的右子树，则父亲的右指向它的右
					//若它是parent的左子树，则父亲的左指向它的左
					if (Rightmin == parent->_left)
						parent->_left = Rightmin->_right;
					else
						parent->_right = Rightmin->_right;
					delete Rightmin;
				}
				return true;
			}
		}
		return false;//cur都为空了还没找到，则该数据不存在
	}

	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}
	//下面的可以放到private里面
	void _InOrder(Node* root)
	{
		if (root == nullptr)
			return;

		_InOrder(root->_left);
		cout << root->_key << " ";
		_InOrder(root->_right);
	}

	   

private:
	Node* _root = nullptr;//可以直接定义,就一个成员变量，无需写个构造函数
};

void testTree()
{
	BSTree<int> t;
	int a[] = { 5,3,4,1,7,8,2,6,0,9 };
	for (auto e : a)
	{//数组是可以用迭代器来遍历的
		t.Insert(e);//插入节点到树中
	}

	t.InOrder();//中序遍历
}

 Test.cpp

#include"BSTree.hpp"

int main()
{
	testTree();

	return 0;
}

三、二叉搜索树的应用

搜索树使用场景：

1、key的模型 ：判断在不在

 比如进入校园要刷校园卡，卡本质里面有芯片，芯片上存储信息，把学校所有学员的信息存到二叉搜索树（因为他的查找效率很高），然后用机器扫描卡，看你卡的信息是否在我的树中，在就让你进

2、key/value的模型：通过key找value 

①、高铁刷身份证

买了票就能进站，刷身份证读的是身份证号码，【key就是身份证，value就是票的信息】然后通过身份证到后台服务器查是否有票的信息，是否是这个车站，这个车次等等，即通过身份证找value

②、中英文互译

中文就是key，英文就是value，即通过中文找英文或通过英文找中文。

③、统计次数

统计次数，即通过一个值找另一个值，用搜索树实现的原因是二叉搜索树的效率高，搜索快

key/value模型的实现只需在我们实现的二叉搜索树中改动一下代码即可，即节点里面除了有key，还有value，但是比较大小的过程还是用key来比较，和value没关系，找到了key就相当于找到了value，因为两者在同一节点中，还要修改的就是Find函数，返回值变成返回节点的指针而不是bool值，因为这样返回的节点既有key又有value

注意：

对于搜索树的修改，搜索树中key是不允许修改的

如果是kv模型的搜索树，可以修改value，但不能修改key，就是因为你改了key就不一定满足二叉搜索树的条件了

kv模型的完整代码：

BSTree.hpp :

//key/value模型
#include<iostream>
#include<string>
using namespace std;

template<class K, class V>
struct BSTreeNode
{
	BSTreeNode(const K& key,const V& value)
		:_key(key)
		,_value(value)
		, _left(nullptr)
		, _right(nullptr)
	{}

	BSTreeNode<K,V>* _left;
	BSTreeNode<K,V>* _right;
	K _key;
	V _value;

};
template<class K, class V>
class BSTree //Binary Search Tree
{
	typedef BSTreeNode<K,V> Node;
public:
	bool Insert(const K& key, const V& value)
	{
		if (_root == nullptr)
		{//若为空树，就给它一个节点
			_root = new Node(key, value);//new是开空间+初始化，所以要调用构造函数，你要写的
			return true;
		}
		Node* cur = _root;//从根节点开始比较
		Node* parent = nullptr;
		while (cur)
		{
			//都会找一个空位置插入，不会说挪动节点来进行插入
			if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;

			}
			else if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{//若在走的过程中遇到相同的数据，返回假，这个数据无法插入
				return false;
			}
		}
		cur = new Node(key,value);//向这个空位置插入数据
		//利用parent的位置与cur连接
		if (parent->_key > key)
			parent->_left = cur;//比根节点小，链接到左边
		else
			parent->_right = cur;//比根节点大，链接到右边
		return true;
	}

	Node* Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key > key)
			{
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				cur = cur->_right;
			}
			else
			{
				return cur;//说明相等，则找到了，返回真
			}
		}
		return nullptr;
	}

	bool Erase(const K& key)
	{
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				//找到了，开始删除
				//1.左为空
				if (cur->_left == nullptr)
				{
					if (cur == _root)
						_root = cur->_right;
					else
					{
						if (parent->_left == cur)
							parent->_left = cur->_right;//cur在父亲的左边，就让父亲的左指向cur的左
						else
							parent->_right = cur->_right;//cur在父亲的右边，就让父亲的右指向cur的右
					}
					delete cur;
				}
				//2.右为空
				else if (cur->_right == nullptr)
				{
					if (cur == _root)
						_root = cur->_left;
					else
					{
						if (parent->_right == cur)
							parent->_right = cur->_left;//cur在父亲的右边，就让父亲的右指向cur的左
						else
							parent->_left = cur->_left;//cur在父亲的左边，就让父亲的左指向cur的右
					}
					delete cur;
				}
				//3.左右都不为空
				else
				{//找左子树的最右节点或右子树的最小节点去替代
				 //这里用右子树的最小节点来替代
					Node* parent = cur;
					Node* Rightmin = cur->_right;//若用右树的最小节点，即右树最左节点
					while (Rightmin->_left)
					{//最左节点的左子树一定为空，故为判断条件
						parent = Rightmin;//替换节点不一定是叶子结点，故还要用parent来链接
						Rightmin = Rightmin->_left;
					}

					cur->_key = Rightmin->_key;//用cur的值来替代
					//转换成删除Rightmin
					//若它是parent的右子树，则父亲的右指向它的右
					//若它是parent的左子树，则父亲的左指向它的左
					if (Rightmin == parent->_left)
						parent->_left = Rightmin->_right;
					else
						parent->_right = Rightmin->_right;
					delete Rightmin;
				}
				return true;
			}
		}
		return false;//cur都为空了还没找到，则该数据不存在
	}

	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}
	//下面的可以放到private里面
	void _InOrder(Node* root)
	{
		if (root == nullptr)
			return;

		_InOrder(root->_left);
		cout << root->_key << ":" <<root->_value << endl;
		_InOrder(root->_right);
	}



private:
	Node* _root = nullptr;//可以直接定义,就一个成员变量，无需写个构造函数
};

void testTree1()
{
	BSTree<string, string>dict;//字典
	dict.Insert("sort", "排序");
	dict.Insert("polynomial", "多项式");
	dict.Insert("femininity", "女性");

	string str;
	while (cin >> str)
	{
		BSTreeNode<string, string>* ret = dict.Find(str);
		if (ret)
		{
			cout << ret->_value << endl;
		}
		else
		{
			cout << "无此单词" << endl;
		}
	}
}

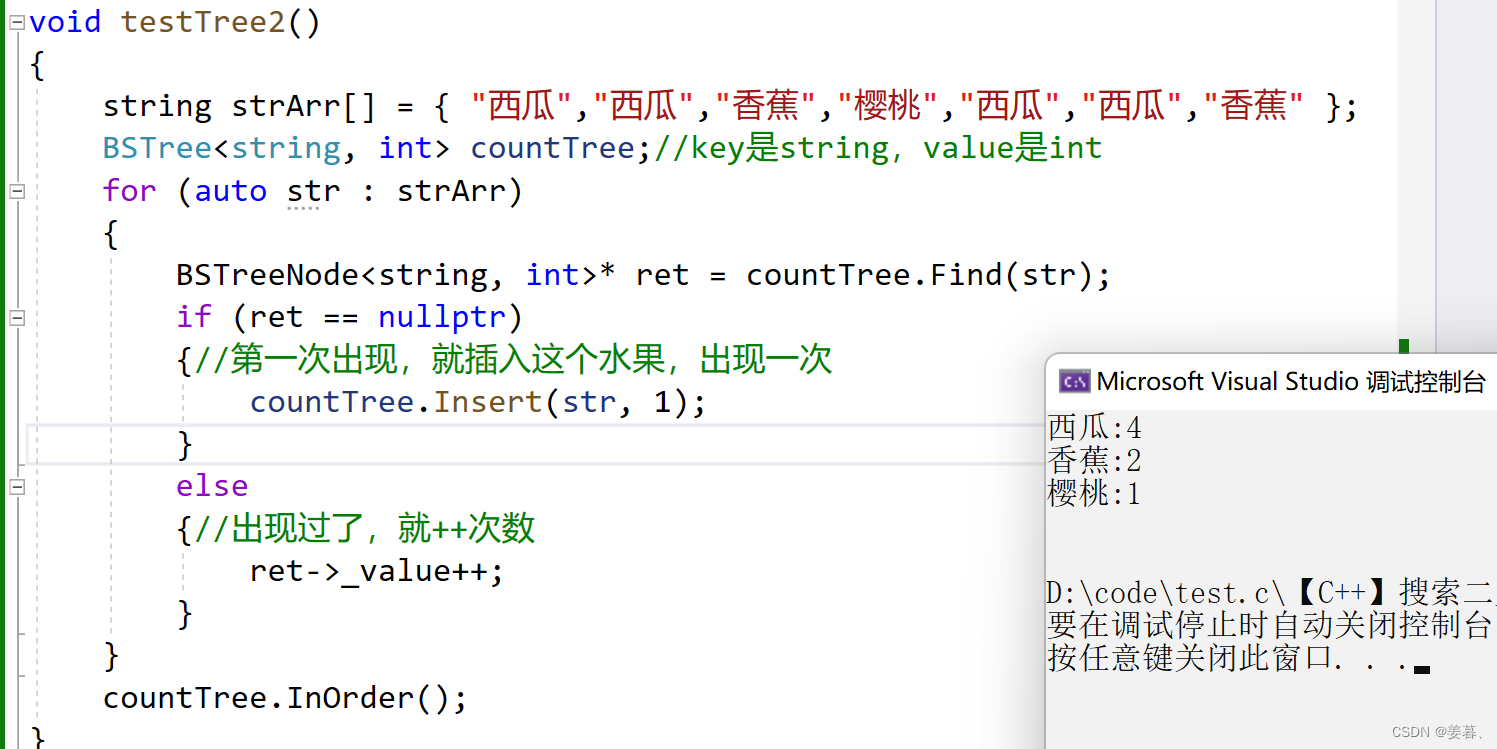
void testTree2()
{
	string strArr[] = { "西瓜","西瓜","香蕉","樱桃","西瓜","西瓜","香蕉" };
	BSTree<string, int> countTree;//key是string，value是int
	for (auto str : strArr)
	{
		BSTreeNode<string, int>* ret = countTree.Find(str);
		if (ret == nullptr)
		{//第一次出现，就插入这个水果，出现一次,因为一开始树为空
			countTree.Insert(str, 1);
		}
		else
		{//出现过了，就++次数
			ret->_value++;
		}
	}
	countTree.InOrder();
}

 Test.cpp

#include"BSTree.hpp"

int main()
{
	//testTree1();
	testTree2();

	return 0;
}

key/value的应用场景

应用场景1--中英文互译

key/value模型测试下面代码逻辑（中英文互译）

 

应用场景2--统计水果出现次数

有一堆水果，请你统计水果出现的次数

 四、二叉搜索树性能分析

 

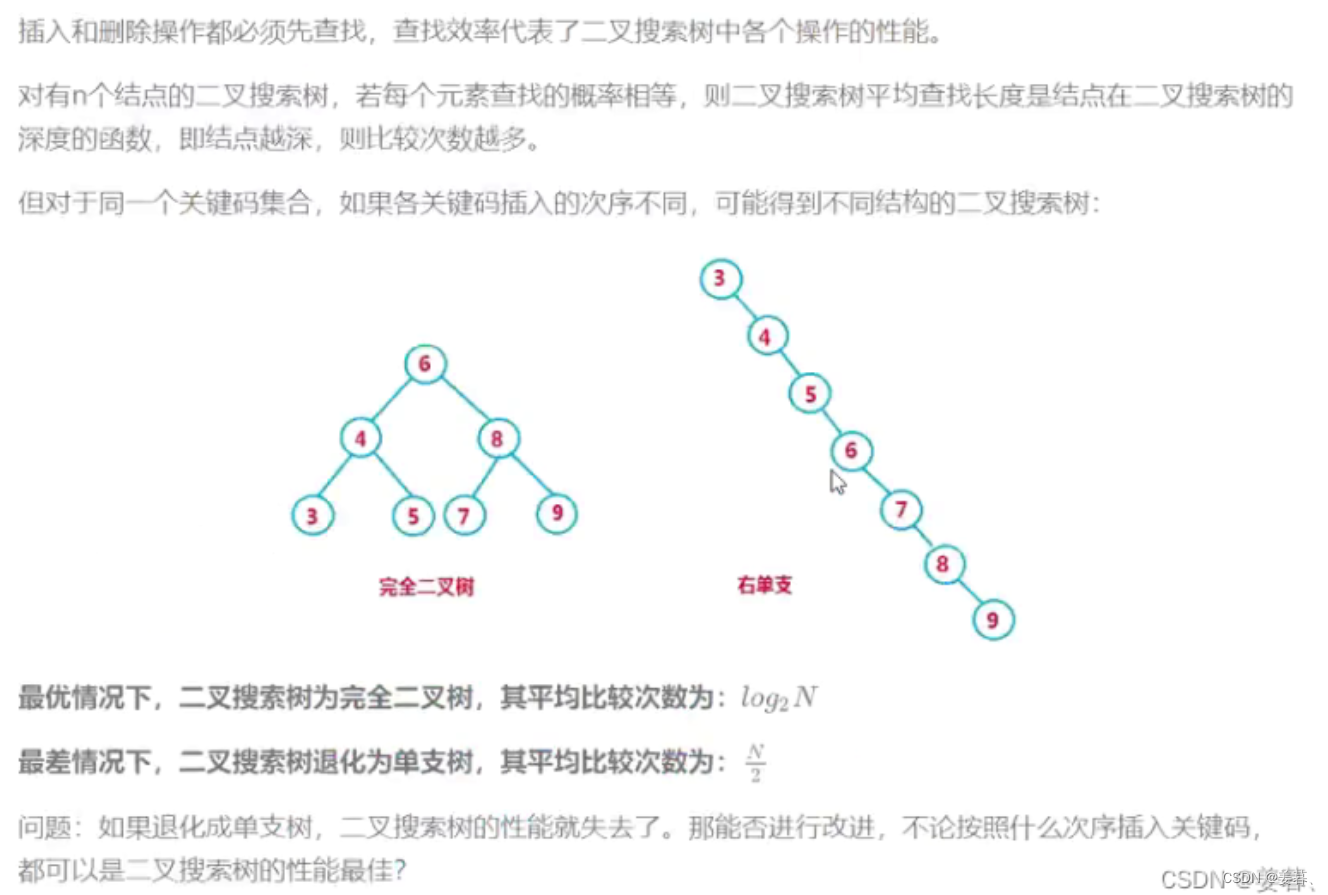
如果插入的数据是有序的或者接近有序的，那么搜索树效率就完全没办法保障

如：1  2  3  4  5  6  7  8，对于树就变成了单支树，搜索树的效率最坏的情况下是O（N）

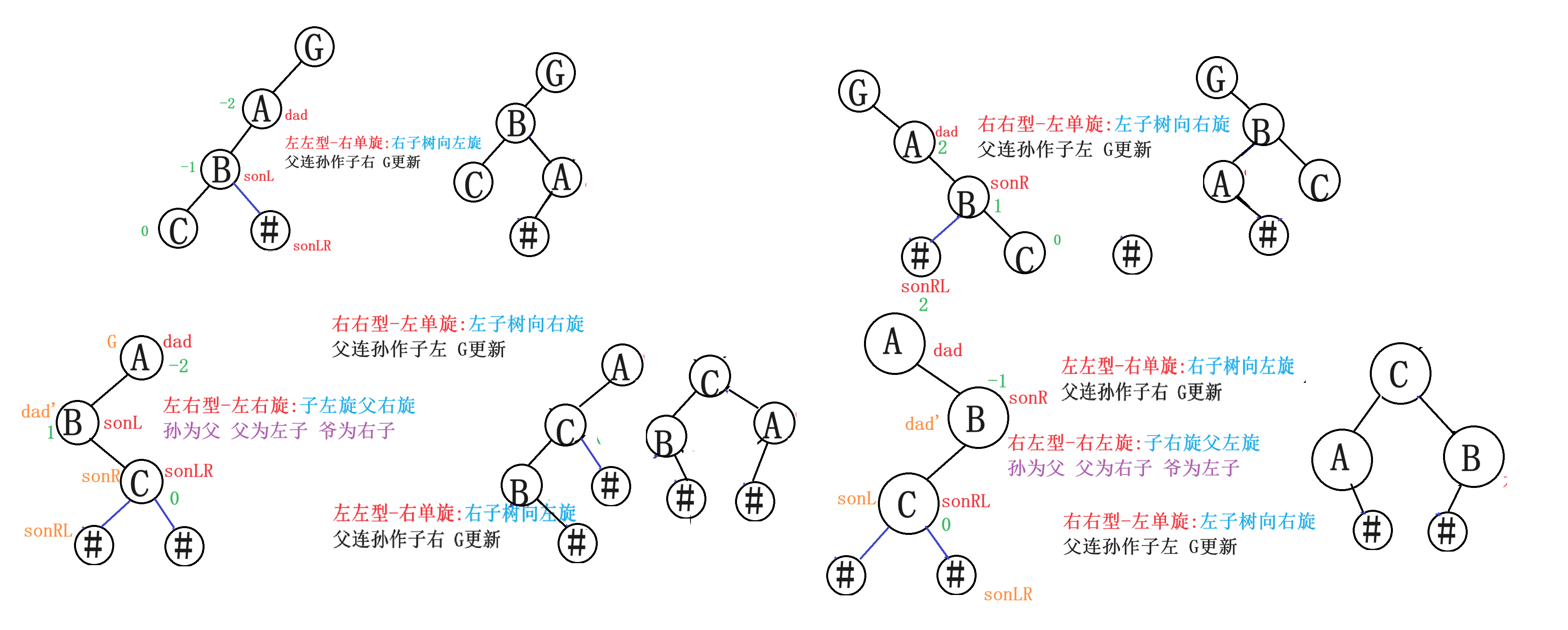
如何解决？平衡树1、AVLTree   2、红黑树

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1051088.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Arthas学习（1）

Arthas学习（1）

1.Arthas作用 Arthas是Alibaba开源的Java诊断工具。 作用&#xff1a;当遇到以下类似问题时&#xff0c;可以帮助我们解决&#xff1a; 1.这个类从哪个jar包加载的&#xff1f;为什么会报各种类相关的Exception? 2.我改的代码为什么没有执行到&#xff1f;难道是我没提交&am…
阅读更多...
浅谈AVL树

浅谈AVL树

文章目录 1.介绍1.1定义1.2来源1.3概念1.特性2.平衡因子[ Balance Factor-- _bf ] 2.BST>AVL1.示例分析2.情况分类3.代码剖析3.1左左型-右单旋3.2右右型-左单旋3.3左右型-左右旋3.4右左型:右左旋3.5总图 3.完整代码3.1AVLTree.h3.2Test.cpp 1.介绍 1.1定义 AVL树 – 平衡二…
阅读更多...
CVE-2020-11978 Apache Airflow 命令注入漏洞分析与利用

CVE-2020-11978 Apache Airflow 命令注入漏洞分析与利用

简介 漏洞软件&#xff1a;Apache Airflow影响版本&#xff1a;< 1.10.10 环境 Vulhub 漏洞测试靶场 复现步骤 进入 /root/vulhub/airflow/CVE-2020-11978/ 目录运行以下命令启动环境 # 初始化数据库 docker compose run airflow-init # 开启服务 docker compose up -…
阅读更多...
字符串常量池位于JVM哪里

字符串常量池位于JVM哪里

Java6 和6之前&#xff0c;常量池是存放在方法区&#xff08;永久代&#xff09;中的。Java7&#xff0c;将常量池是存放到了堆中。Java8 之后&#xff0c;取消了整个永久代区域&#xff0c;取而代之的是元空间。运行时常量池和静态常量池存放在元空间中&#xff0c;而字符串常…
阅读更多...
web：[ACTF2020 新生赛]Upload

web：[ACTF2020 新生赛]Upload

题目 点进页面&#xff0c;是一个文件上传&#xff0c;能联想到getshell 先尝试随便上传一个文件试试 显示上传的文件以jpg、png、gif结尾的图片 构造一句话木马&#xff0c;再将文件后缀改为jpg <?php eval($_POST[1234]);?> 显示上传成功&#xff0c;但是显示无法…
阅读更多...
MySQL学习笔记24

MySQL学习笔记24

MySQL的物理备份&#xff1a; xtrabackup备份介绍&#xff1a; xtrabackup优缺点&#xff1a; 优点&#xff1a; 1、备份过程快速、可靠&#xff08;因为是物理备份&#xff09;&#xff1b;直接拷贝物理文件。 2、支持增量备份&#xff0c;更为灵活&#xff1b; 3、备份…
阅读更多...
【数据结构】——顺序表详解

【数据结构】——顺序表详解

大家好&#xff01;当我们学习了动态内存管理后&#xff0c;就可以写一个管理数据的顺序表了&#xff01;&#xff01;&#xff01; 顺序表的理解&#xff1a; 线性表是最基本、最简单、也是最常用的一种数据结构。线性表&#xff08;linear list&#xff09;是数据结构的一种…
阅读更多...
self-attention、transformer、bert理解

self-attention、transformer、bert理解

参考李宏毅老师的视频 https://www.bilibili.com/video/BV1LP411b7zS?p2&spm_id_frompageDriver&vd_sourcec67a2725ac3ca01c38eb3916d221e708 一个输入&#xff0c;一个输出&#xff0c;未考虑输入之间的关系&#xff01;&#xff01;&#xff01; self-attention…
阅读更多...
CSS详细基础（三）复合选择器

CSS详细基础（三）复合选择器

前两章介绍了CSS中的基础属性&#xff0c;以及一些基础的选择器&#xff0c;本贴开始介绍复合选择器的内容~ ​ 在 CSS 中&#xff0c;可以根据选择器的类型把选择器分为基础选择器和复合选择器&#xff0c;复合选择器是建立在基础选择器之上&#xff0c;对基本选择器进行组合形…
阅读更多...
c语言练习70:反转两次的数字

c语言练习70:反转两次的数字

反转两次的数字 题⽬描述&#xff1a; 反转 ⼀个整数意味着倒置它的所有位。 例如&#xff0c;反转 2021 得到 1202 。反转 12300 得到 321 &#xff0c;不保留前导零 。 给你⼀个整数 num &#xff0c;反转 num 得到 reversed1 &#xff0c;接着反转 reversed1 得到 revers…
阅读更多...
使用KEIL自带的仿真器仿真遇到问题解决

使用KEIL自带的仿真器仿真遇到问题解决

*** error 65: access violation at 0x40021000 : no read permission 修改debug选项设置为下方内容。
阅读更多...
Java之多线程的生产者消费者问题的详细解析

Java之多线程的生产者消费者问题的详细解析

3.生产者消费者 3.1生产者和消费者模式概述【应用】 概述 生产者消费者模式是一个十分经典的多线程协作的模式&#xff0c;弄懂生产者消费者问题能够让我们对多线程编程的理解更加深刻。 所谓生产者消费者问题&#xff0c;实际上主要是包含了两类线程&#xff1a; 一类是生产者…
阅读更多...
MJ 种的摄影提示词关键字

MJ 种的摄影提示词关键字

景别 Front view photo 正面照 Front view photo of a Boston Terrier with smileSide view photo 侧身照 Side view photo of a Boston Terrier with smileBack view photo 背影照 Back view photo of a Boston TerrierFull body 全身照 Full body photo of a Boston Ter…
阅读更多...
electron之快速上手

electron之快速上手

前一篇文章已经介绍了如何创建一个electron项目&#xff0c;没有看过的小伙伴可以去实操一下。 接下来给大家介绍一下electron项目的架构是什么样的。 electron之快速上手 electron项目一般有两个进程&#xff1a;主进程和渲染进程。 主进程&#xff1a;整个项目的唯一入口&…
阅读更多...
2.物联网射频识别，RFID通信原理，RFID读写器与标签无线交互方式、数据反馈方式，RFID调制与解调、编码方式，不同RFID标签与读写器

2.物联网射频识别，RFID通信原理，RFID读写器与标签无线交互方式、数据反馈方式，RFID调制与解调、编码方式，不同RFID标签与读写器

一。RFID无线识别的原理 1.RFID系统无线通信基本原理 如下图所示&#xff0c;左边是读写器&#xff08;刷卡器&#xff09;&#xff0c;右边是标签&#xff08;卡&#xff09;&#xff0c;中间通过无线通信方式。 标签&#xff1a;&#xff08;卡&#xff09; 读写器&#xff…
阅读更多...
Sound/播放提示音, Haptics/触觉反馈, LocalNotification/本地通知 的使用

Sound/播放提示音, Haptics/触觉反馈, LocalNotification/本地通知 的使用

1. Sound 播放提示音 1.1 音频文件: tada.mp3&#xff0c; badum.mp3 1.2 文件位置截图: 1.3 实现 import AVKit/// 音频管理器 class SoundManager{// 单例对象 Singletonstatic let instance SoundManager()// 音频播放var player: AVAudioPlayer?enum SoundOption: Stri…
阅读更多...
python二维码识别tesseract

python二维码识别tesseract

window安装tesseract 下载路径&#xff1a; https://digi.bib.uni-mannheim.de/tesseract/ 选择 双击安装在D:\sore\teeseract-OCR后&#xff1a; 配置环境变量 配置环境变量Path&#xff1a;D:\sore\teeseract-OCR 配置语言包的环境变量TESSDATA_PREFIX&#xff1a; D:\s…
阅读更多...
搭建自己的搜索引擎之五

搭建自己的搜索引擎之五

一、前言 接上文 搭建自己的搜索引擎之四&#xff0c;下面继续介绍茴香豆茴字的另外两种写法。 二、Jest Jest是ES的Java Http Rest客户端&#xff0c;它主要是为了弥补以前ES自有API缺少HttpRest接口客户端的不足&#xff0c;但因为现在ES官方已经提供了RestClient ,该项目已…
阅读更多...
Dynamic CRM开发 - 实体窗体（二）主窗体

Dynamic CRM开发 - 实体窗体（二）主窗体

主窗体是功能最丰富，使用场景最多的窗体。 主窗体界面如下图： 下面按照图中的序号，简述一下窗体的主要功能： 0、窗体的主要布局部分，即用户看到的内容，可以拖动右侧的字段到窗体中想要放置的地方。 默认有标题、常规（选项卡）、页脚三部分，常规处于高亮状态，即可以…
阅读更多...
第十二章 类和对象

第十二章 类和对象

C面向对象的三大特性为&#xff1a;封装、继承、多态 C认为万事万物都皆为对象&#xff0c;对象上有其属性和行为 例如&#xff1a; 人可以作为对象&#xff0c;属性有姓名、年龄、身高、体重...&#xff0c;行为有走、跑、跳、吃饭、唱歌... 车也可以作为对象&#xff0c;…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023