self-attention、transformer、bert理解

news2024/11/24 9:14:59

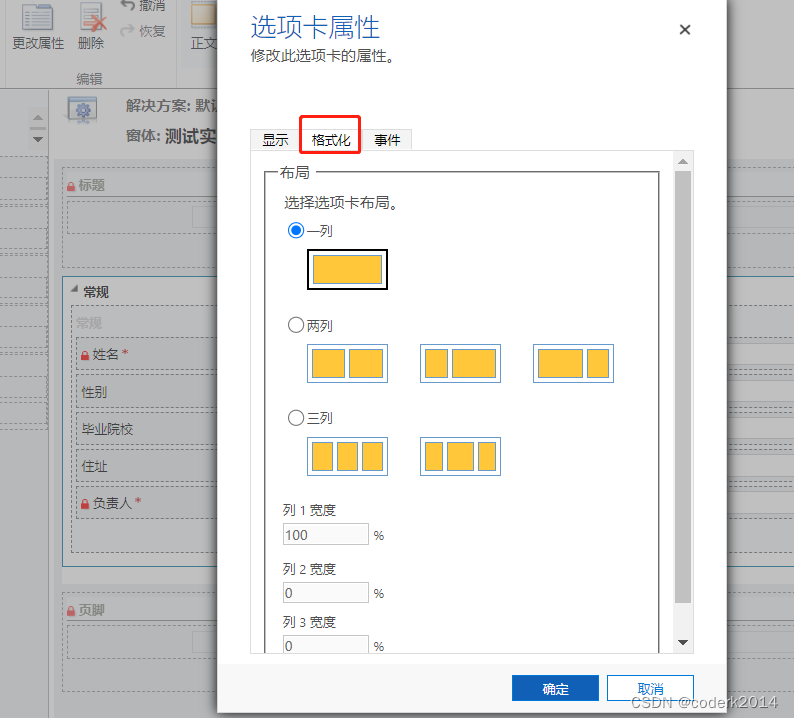
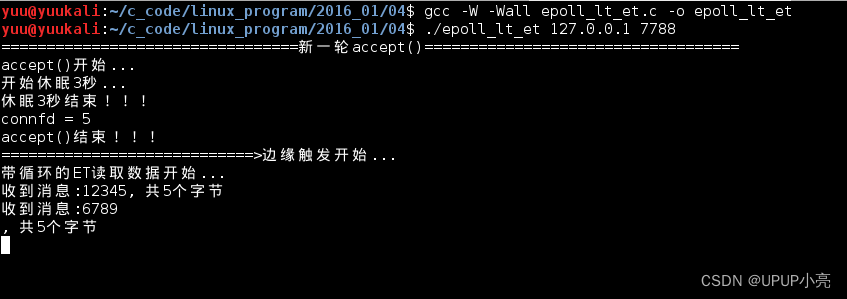
参考李宏毅老师的视频 https://www.bilibili.com/video/BV1LP411b7zS?p=2&spm_id_from=pageDriver&vd_source=c67a2725ac3ca01c38eb3916d221e708
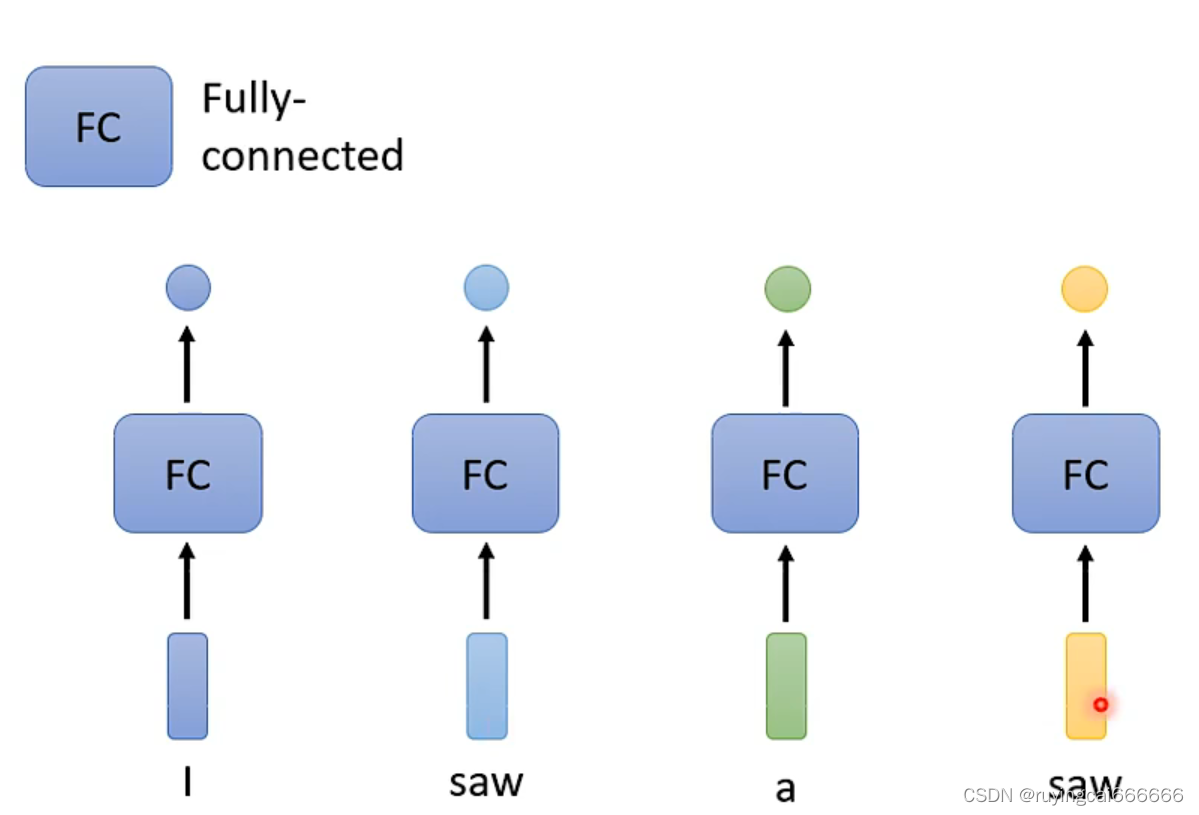
在这里插入图片描述
一个输入，一个输出，未考虑输入之间的关系！！！
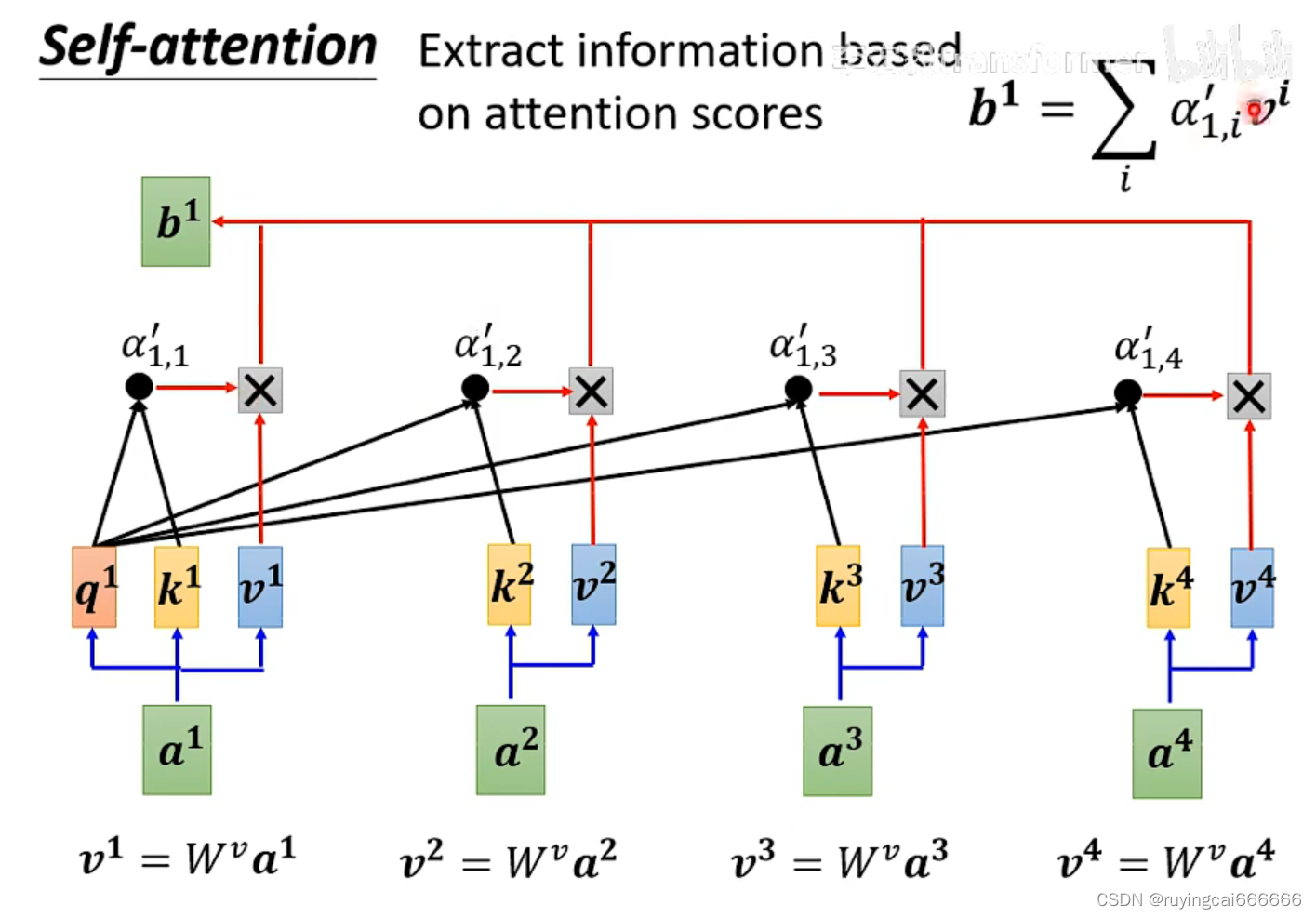
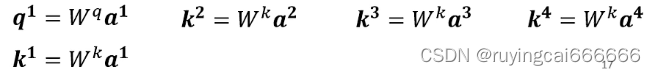
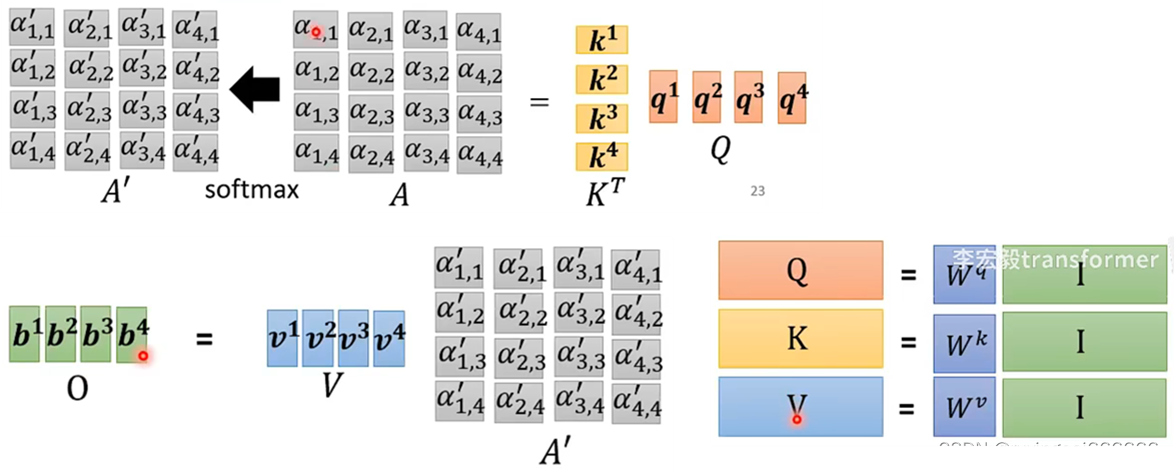
在这里插入图片描述
在这里插入图片描述

self-attention考虑输入之间的关系，关于a1的输出b1的计算方法如上图所示，如此类推计算b2，b3，b4，合并考虑整体计算公式如下图所示，就是找出Wq，Wk和Wv。
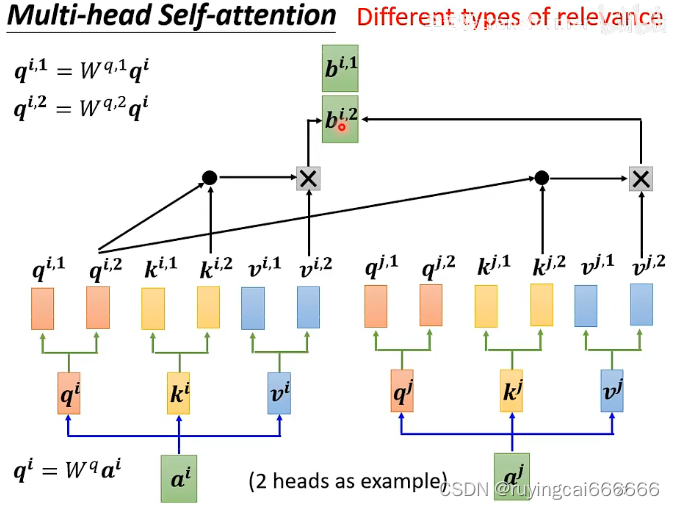
在这里插入图片描述
multi-head attention：
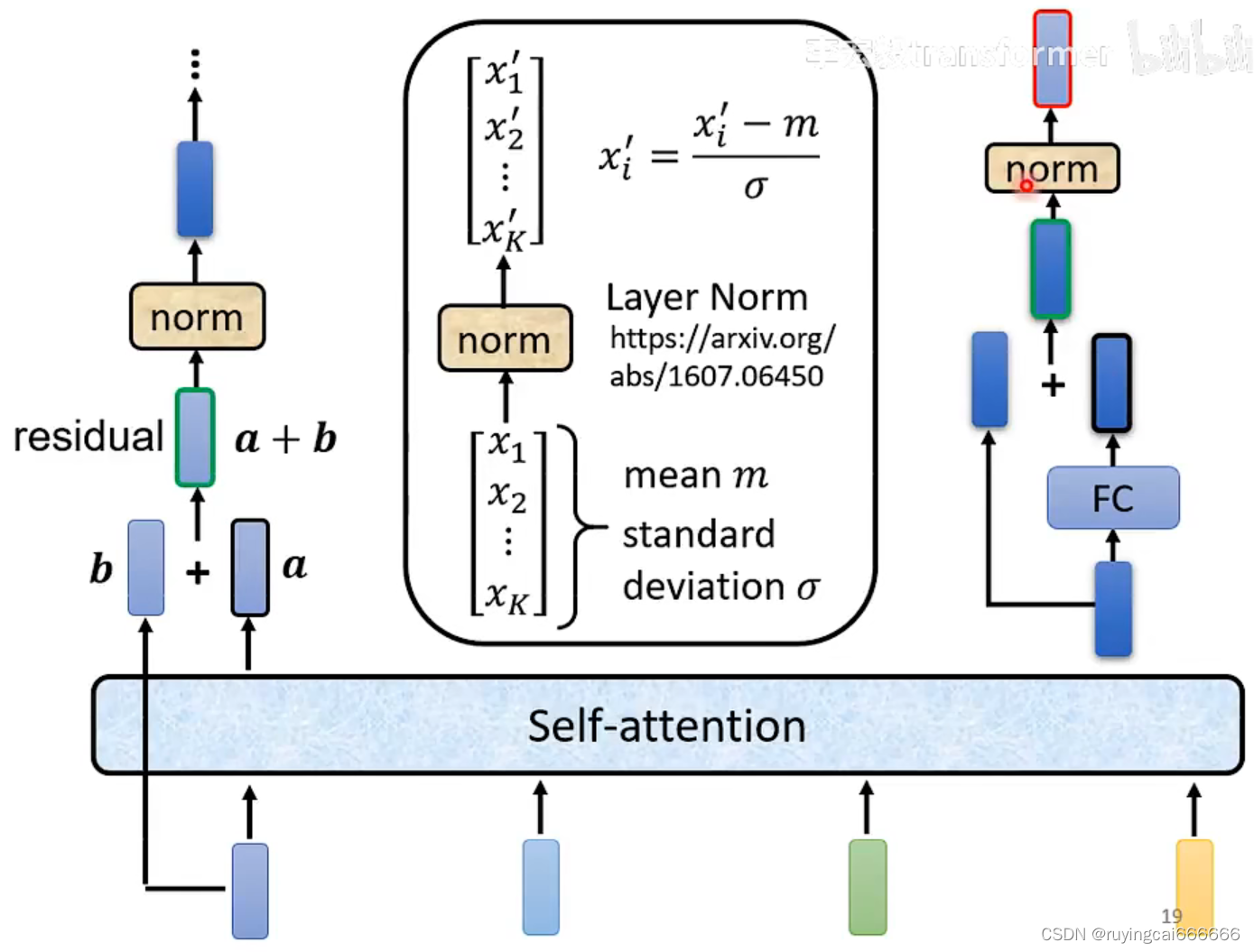
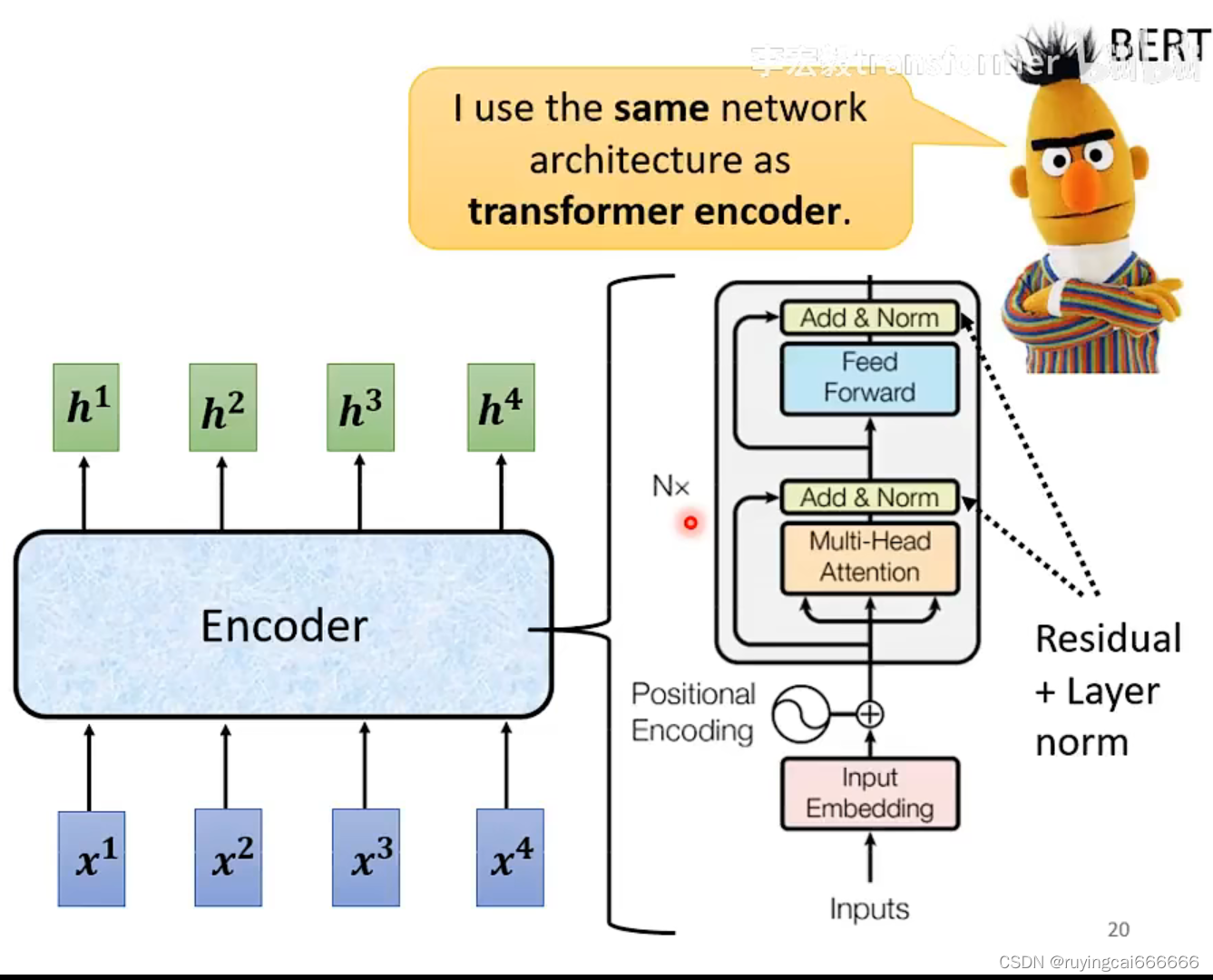
在这里插入图片描述
transformer：
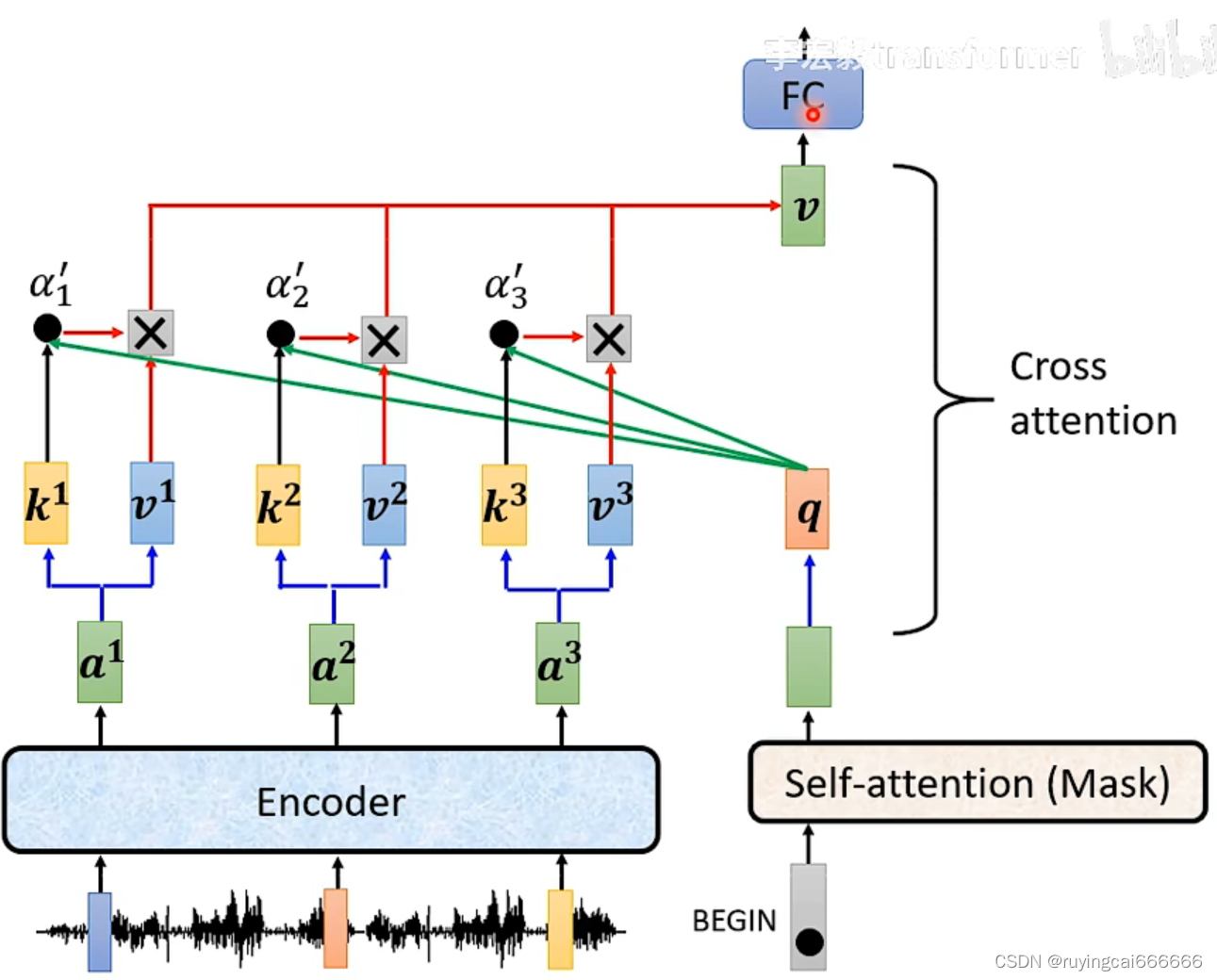
在这里插入图片描述
在这里插入图片描述
cross attention：
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1051078.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

CSS详细基础（三）复合选择器

CSS详细基础（三）复合选择器

前两章介绍了CSS中的基础属性，以及一些基础的选择器，本贴开始介绍复合选择器的内容~ ​ 在 CSS 中，可以根据选择器的类型把选择器分为基础选择器和复合选择器，复合选择器是建立在基础选择器之上，对基本选择器进行组合形…
阅读更多...
c语言练习70:反转两次的数字

c语言练习70:反转两次的数字

反转两次的数字 题⽬描述： 反转 ⼀个整数意味着倒置它的所有位。 例如，反转 2021 得到 1202 。反转 12300 得到 321 ，不保留前导零 。 给你⼀个整数 num ，反转 num 得到 reversed1 ，接着反转 reversed1 得到 revers…
阅读更多...
使用KEIL自带的仿真器仿真遇到问题解决

使用KEIL自带的仿真器仿真遇到问题解决

*** error 65: access violation at 0x40021000 : no read permission 修改debug选项设置为下方内容。
阅读更多...
Java之多线程的生产者消费者问题的详细解析

Java之多线程的生产者消费者问题的详细解析

3.生产者消费者 3.1生产者和消费者模式概述【应用】 概述 生产者消费者模式是一个十分经典的多线程协作的模式，弄懂生产者消费者问题能够让我们对多线程编程的理解更加深刻。 所谓生产者消费者问题，实际上主要是包含了两类线程： 一类是生产者…
阅读更多...
MJ 种的摄影提示词关键字

MJ 种的摄影提示词关键字

景别 Front view photo 正面照 Front view photo of a Boston Terrier with smileSide view photo 侧身照 Side view photo of a Boston Terrier with smileBack view photo 背影照 Back view photo of a Boston TerrierFull body 全身照 Full body photo of a Boston Ter…
阅读更多...
electron之快速上手

electron之快速上手

前一篇文章已经介绍了如何创建一个electron项目，没有看过的小伙伴可以去实操一下。 接下来给大家介绍一下electron项目的架构是什么样的。 electron之快速上手 electron项目一般有两个进程：主进程和渲染进程。 主进程：整个项目的唯一入口&…
阅读更多...
2.物联网射频识别，RFID通信原理，RFID读写器与标签无线交互方式、数据反馈方式，RFID调制与解调、编码方式，不同RFID标签与读写器

2.物联网射频识别，RFID通信原理，RFID读写器与标签无线交互方式、数据反馈方式，RFID调制与解调、编码方式，不同RFID标签与读写器

一。RFID无线识别的原理 1.RFID系统无线通信基本原理 如下图所示，左边是读写器（刷卡器），右边是标签（卡），中间通过无线通信方式。 标签：（卡） 读写器&#xff…
阅读更多...
Sound/播放提示音, Haptics/触觉反馈, LocalNotification/本地通知 的使用

Sound/播放提示音, Haptics/触觉反馈, LocalNotification/本地通知 的使用

1. Sound 播放提示音 1.1 音频文件: tada.mp3， badum.mp3 1.2 文件位置截图: 1.3 实现 import AVKit/// 音频管理器 class SoundManager{// 单例对象 Singletonstatic let instance SoundManager()// 音频播放var player: AVAudioPlayer?enum SoundOption: Stri…
阅读更多...
python二维码识别tesseract

python二维码识别tesseract

window安装tesseract 下载路径： https://digi.bib.uni-mannheim.de/tesseract/ 选择 双击安装在D:\sore\teeseract-OCR后： 配置环境变量 配置环境变量Path：D:\sore\teeseract-OCR 配置语言包的环境变量TESSDATA_PREFIX： D:\s…
阅读更多...
搭建自己的搜索引擎之五

搭建自己的搜索引擎之五

一、前言 接上文 搭建自己的搜索引擎之四，下面继续介绍茴香豆茴字的另外两种写法。 二、Jest Jest是ES的Java Http Rest客户端，它主要是为了弥补以前ES自有API缺少HttpRest接口客户端的不足，但因为现在ES官方已经提供了RestClient ,该项目已…
阅读更多...
Dynamic CRM开发 - 实体窗体（二）主窗体

Dynamic CRM开发 - 实体窗体（二）主窗体

主窗体是功能最丰富，使用场景最多的窗体。 主窗体界面如下图： 下面按照图中的序号，简述一下窗体的主要功能： 0、窗体的主要布局部分，即用户看到的内容，可以拖动右侧的字段到窗体中想要放置的地方。 默认有标题、常规（选项卡）、页脚三部分，常规处于高亮状态，即可以…
阅读更多...
第十二章 类和对象

第十二章 类和对象

C面向对象的三大特性为：封装、继承、多态 C认为万事万物都皆为对象，对象上有其属性和行为 例如： 人可以作为对象，属性有姓名、年龄、身高、体重...，行为有走、跑、跳、吃饭、唱歌... 车也可以作为对象，…
阅读更多...
docker安装apisix全教程包含windows和linux

docker安装apisix全教程包含windows和linux

docker安装apisix 一、Windows安装1、首先需要安装docker和docker compose，如果直接安装docker desktop，会自动安装docker compose。2、重新启动电脑3、访问 Docker 的下载（[https://www.docker.com/products/docker-desktop](https://www.do…
阅读更多...
RocketMQ 版本升级测试

RocketMQ 版本升级测试

一、背景 RocketMQ 版本升级，3.6.4升级到5.1.3。 二、机器资源 应用端： 10.XX.67.249【机器 1】 cd /home/product/logs/dolphin_task_test_logs/ vim info.logMQ 服务端： 旧MQ 10.XX.108.249 broker-001。用于测试升级NameServer【机器 2…
阅读更多...
react库的基础学习

react库的基础学习

React介绍 React.js是前端三大新框架：Angular.js、React.js、Vue.js之一，这三大新框架的很多理念是相同的，但是也有各自的特点。 React起源于Facebook的内部项目，因为该公司对市场上所有 JavaScript MVC 框架，都不满…
阅读更多...
【数据库】形式化关系查询语言（一）：关系代数Relational Algebra

【数据库】形式化关系查询语言（一）：关系代数Relational Algebra

目录 一、关系代数Relational Algebra 1. 基本运算 a. 选择运算（Select Operation） b. 投影运算（Project Operation） 组合 c. 并运算（Union Operation） d. 集合差运算（Set Difference Op…
阅读更多...
【C++】vector基本接口介绍

【C++】vector基本接口介绍

vector接口目录： 一、vector的初步介绍 1.1vector和string的联系与不同 1.2 vector的源码参数 二、vector的四种构造（缺省填充元素迭代器拷贝构造） 三、vecto的扩容操作与机制 3.1resize（老朋友了，不会就去看str…
阅读更多...
Linux文件查找，别名，用户组综合练习

Linux文件查找，别名，用户组综合练习

1.文件查看: 查看/etc/passwd文件的第5行 [rootserver ~]# head -5 /etc/passwd root:x:0:0:root:/root:/bin/bash bin:x:1:1:bin:/bin:/sbin/nologin daemon:x:2:2:daemon:/sbin:/sbin/nologin adm:x:3:4:adm:/var/adm:/sbin/nologin lp:x:4:7:lp:/var/spool/lpd:/sbin/nologi…
阅读更多...
epoll与socket缓冲区的恩恩怨怨

epoll与socket缓冲区的恩恩怨怨

文章目录 前言一、什么是socket缓冲区二、阻塞与非阻塞内核缓冲区1、如果发送缓冲区满了会怎么样阻塞非阻塞 2、如果接受缓冲区为空会怎么样阻塞非阻塞 三、epoll与缓冲区的恩恩怨怨水平触发边缘触发非阻塞阻塞 结论 前言 本文深挖网络编程中的缓冲区，从什么是缓冲…
阅读更多...
排序：基数排序算法分析

排序：基数排序算法分析

1.算法思想 假设长度为n的线性表中每个结点aj的关键字由d元组 ( k j d − 1 , k j d − 2 , k j d − 3 , . . . , k j 1 , k j 0 ) (k_{j}^{d-1},k_{j}^{d-2},k_{j}^{d-3},... ,k_{j}^{1} ,k_{j}^{0}) (kjd−1​,kjd−2​,kjd−3​,...,kj1​,kj0​)组成， 其中&am…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023