目录
- 一、双指针
- 双指针与链表
- 双指针与链表
- 二、前缀和
- 一维
- 二维
- 三、差分
- 一维
- 二维
- 四、深度搜索,dfs
- dfs+数组排列
- dfs+岛屿问题
- dfs+染色法(二分图判定)
- dfs+路径规划
- dfs+拓扑排序
- 五、广度搜索,bfs
- bfs+最优路径规划
- bfs+dijkstra
- 六、单调栈
- 七、滑动窗口
- 八、单调队列
- 九、基础图算法
- 并查集+kruskal
一、双指针
1、双指针与链表
- 链表的合并、链表是否有环、链表的倒数第K个节点都可以用双指针来实现,但不一定是最好的方法。
2、双指针与数组
- 在原数组的基础上剔除一些元素就可以用双指针来实现。
二、前缀和
1、一维
- 前缀和:
S i = a i + a i − 1 + . . . + a 0 S{\tiny i} = a{\tiny i} +a{\tiny i-1}+...+a{\tiny 0} Si=ai+ai−1+...+a0
S n 就被称为 a n 的前缀和,要求 a m 到 a n 之间的和就是 S n − S m S{\tiny n}就被称为a{\tiny n}的前缀和,要求a{\tiny m}到a{\tiny n}之间的和就是S{\tiny n}-S{\tiny m} Sn就被称为an的前缀和,要求am到an之间的和就是Sn−Sm- 题目链接:一维前缀和
#include<iostream> using namespace std; const int N = 100010; int a[N]; long long S[N]; int main() { int n,q; cin >> n >> q; for(int i = 1; i <= n; i++) { cin >> a[i];//数据比较大的话比scanf耗时间 S[i] = S[i-1]+a[i]; } for(int i = 0; i < q; i++) { int l,r; cin >> l >> r; cout << S[r]-S[l-1] << endl; } return 0; }
2、二维
-
上面前缀和是一维数组的情况下,如果是二维数组的话又是另一种情况了。
-
红框元素和 = 蓝框元素和 + 绿框元素和 - 紫框元素和 + 黄色框的元素。这个是构造前缀和,如果你是每次遍历这个矩阵内的元素相加求和的话时间复杂度就会非常高。
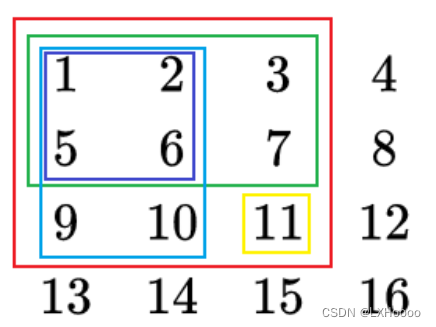
-
构造如上的前缀和数组之后就可以解决下面的问题。我任意从矩阵找了一个范围就如图中红框,要求红框中的元素和。
-
红框元素和 = 黑框元素和 - 蓝框元素和 - 绿框元素和 + 黄框元素和。这就可以用到上面构造好的前缀和数组。
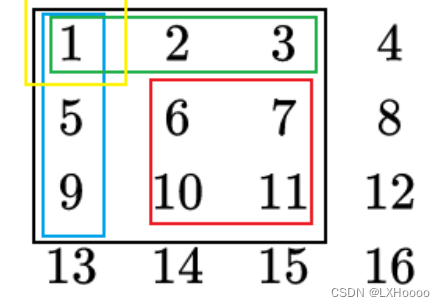
- 题目链接:二维前缀和
#include<iostream> using namespace std; const int N = 1010; long long a[N][N],S[N][N]; int main() { int m,n,q; cin >> m >> n >> q; for(int i = 1; i <= m; i++) { for(int j = 1; j <= n; j++) { cin >> a[i][j]; S[i][j] = S[i][j-1] + S[i-1][j] - S[i-1][j-1] + a[i][j]; } } for(int i = 0; i < q; i++) { int x1,y1,x2,y2; cin >> x1 >> y1 >> x2 >> y2; cout << S[x2][y2] - S[x2][y1-1] - S[x1-1][y2] + S[x1-1][y1-1] << endl; } return 0; }
三、差分
1、一维
- 差分:输入的数组 a n a{\tiny n} an,用 a n a{\tiny n} an数组构造 b n b{\tiny n} bn数组, a n a{\tiny n} an就叫做 b n b{\tiny n} bn的前缀和,相反 b n b{\tiny n} bn就叫做 a n a{\tiny n} an的差分
b = a{\tiny 1}\\
b{\tiny 2} = a{\tiny 2}-a{\tiny 1}\\
...\\
b{\tiny n}=a{\tiny n}-a{\tiny n-1}\\
推得:a{\tiny i}=b{\tiny 1}+b{\tiny 2}+...+b{\tiny i}
- 这种一般用来解决的题型是将
a
l
−
a
r
a{\tiny l}-a{\tiny r}
al−ar这一段元素每个元素加上k,只需要
b
l
+
k
,
b
r
+
1
−
k
b{\tiny l}+k,b{\tiny r+1}-k
bl+k,br+1−k,再将
b
n
b{\tiny n}
bn求前缀和就实现了将
a
n
a{\tiny n}
an数组的l-r这一段上的元素加上k。
- 题目链接:拼车
class Solution { public: bool carPooling(vector<vector<int>>& trips, int capacity) { int b[1001] = {0};//差分数组 for(auto tmp:trips) { int numP = tmp[0]; int from = tmp[1]; int to = tmp[2]; b[from] += numP; b[to] -= numP;//因为在to就下了,所以这一点就要减去而不是to+1减去 } if(b[0] > capacity) { return false; } for(int i = 1; i <= 1000; i++) { b[i] = b[i-1] + b[i]; if(b[i] > capacity) { return false; } } return true; } };
2、二维
-
二维差分和二维前缀和不同,二维前缀和是求任意一块区域内的元素和,而二维差分则是在任意一块区域内加上或者减去某个数。
-
如下图,只在红框的这块区域加上k,则只需将蓝框和绿框的区域减去k,蓝框绿框重叠的部分多减了一次,需要加上K。只需要找到红框的左上角{x1,y1}和右下角{x2,y2}两个点就可以实现。
b [ x 1 ] [ y 1 ] + = c b [ x 2 + 1 ] [ y 1 ] − = c b [ x 1 ] [ y 2 + 1 ] − = c b [ x 2 + 1 ] [ y 2 + 1 ] + = c b[x1][y1]+= c\\ b[x2+1][y1] -= c\\ b[x1][y2+1] -= c\\ b[x2+1][y2+1] += c b[x1][y1]+=cb[x2+1][y1]−=cb[x1][y2+1]−=cb[x2+1][y2+1]+=c
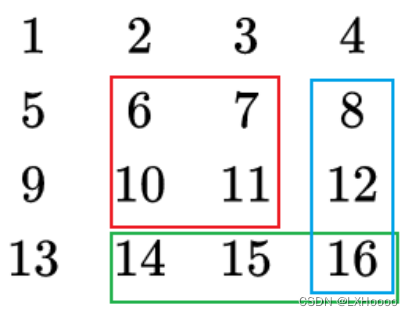
-
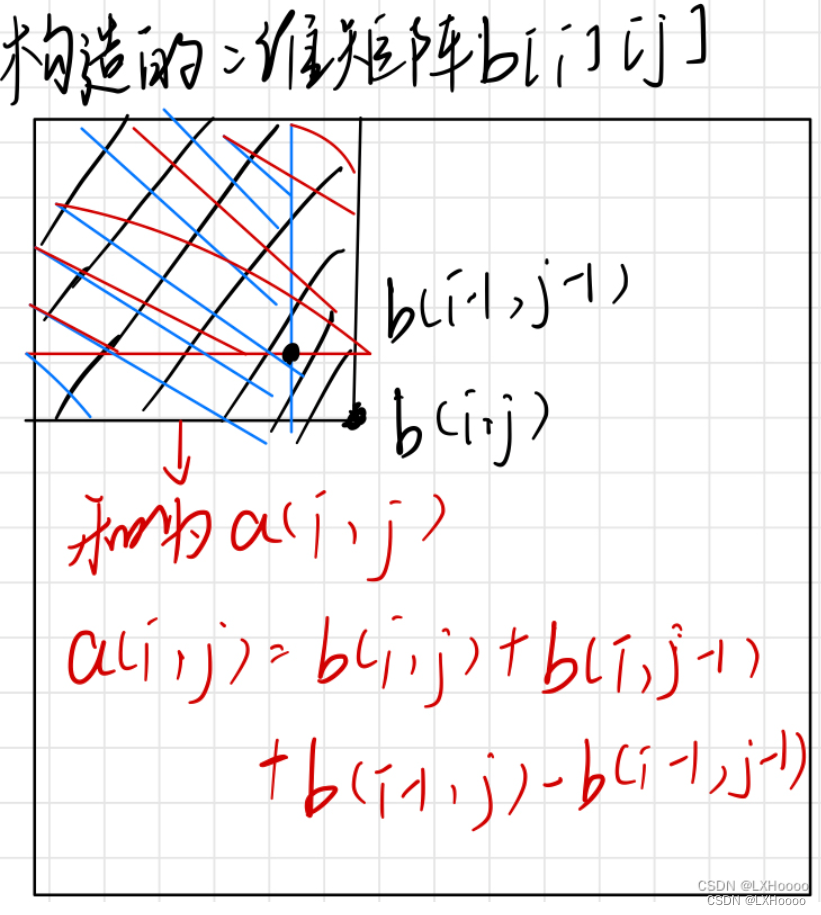
上面构造了差分数组,现在要求出红框区域的和就是按照前缀和来求行了。
-
这个前缀和并不是区域内所有元素的和,而是如下图所示。
四、深度搜索(DFS,空间复杂度比BFS低)
1、dfs+数组
- 组合:元素无重不可复选
nums = [1,2,3] 子集:[ [],[1],[2],[3],[1,2],[1,3],[2,3],[1,2,3] ]- 题目链接:子集
class Solution { public: vector<vector<int>>ret; vector<int>track; vector<vector<int>> subsets(vector<int>& nums) { backtrack(nums,0); return ret; } void backtrack(vector<int>&nums,int start) { ret.push_back(track); //这个i = start是控制不重复的关键 for(int i = start; i < nums.size(); i++) { track.push_back(nums[i]); backtrack(nums,i+1); track.pop_back(); } } }; - 排列:元素无重不可复选
nums = [1,2,3] 全排列: [ [1,2,3],[1,3,2], [2,1,3],[2,3,1], [3,1,2],[3,2,1] ]- 题目链接:全排列
class Solution { public: vector<bool>used;//防止重复选元素 vector<int>tmp; vector<vector<int>>ret; void dfs(vector<int>&nums) { for(int i = 0; i < nums.size(); i++) { if(tmp.size() == nums.size()) { ret.push_back(tmp); return; } if(used[i]) { continue; } tmp.push_back(nums[i]); used[i] = true; dfs(nums); tmp.pop_back(); used[i] = false; } } vector<vector<int>> permute(vector<int>& nums) { int n = nums.size(); used.resize(n,false); dfs(nums); return ret; } };
2、dfs+岛屿问题
- 这种岛屿问题,思路都是找到了一个陆地,然后dfs把和它相连的所有陆地都遍历一遍,遍历完之后并记录已经遍历过,之后不再遍历。
- 题目链接:求岛屿数量
class Solution{ public: int numIslands(vector<vector<char>>&grid) { int m = grid.size(), n = grid[0].size(); int ret = 0; for(int i = 0; i < m; i++) { for(int j = 0; j < n; j++) { //遇到了一个陆地,就要去dfs扩展 if(grid[i][j] == '1') { ret++; dfs(grid,i,j); } } } return ret; } void dfs(vector<vector<char>>&grid,int i,int j) { int m = grid.size(), n = grid[0].size(); if(i < 0 || j < 0 || i >= m || j >= n) { return; } if(grid[i][j] == '0') { return; } grid[i][j] = '0'; //扩展下右上左四个方向 dfs(grid,i+1,j); dfs(grid,i,j+1); dfs(grid,i-1,j); dfs(grid,i,j-1); } };
3、dfs+染色法(二分图判定)
- 二分图就是相邻节点互相矛盾的意思,用染色法来做,就是相邻节点染的颜色要不一样,否则就不是二分图。
- 题目链接:二分图
class Solution{ private: bool ok = true; vector<bool>color; vector<bool>visited; public: bool isBipartite(vector<vector<int>>&graph) { int n = graph.size(); visited.resize(n,false); color.resize(n,false); for(int v = 0; v < n; v++) { if(!visited[v]) { traverse(graph,v); } } return ok; } void traverse(vector<vector<int>>&graph,int v) { if(!ok) { return; } visited[v] = true; for(auto w:graph[v]) { if(!visited[w]) { color[w] = !color[v]; traverse(graph,w); } else { if(color[v] == color[w]) { ok = false; return; } } } } };
4、dfs+路径规划
- 这种和bfs求最优路径不一样,这种一般是中间有障碍物,寻找能够到达目的地的路径,如果是网格带权重的用dfs和bfs都不太合适,这个时候动态规划是比较合适的。
- 题目链接:路径规划
class Solution { public: vector<vector<bool>>visited; vector<vector<int>>tmp; bool arrival = false; void dfs(vector<vector<int>>&obstacleGrid,int x,int y,int m,int n) { if(x < 0 || x >= m || y < 0 || y >= n) { return; } if(arrival || visited[x][y] || obstacleGrid[x][y] == 1) { return; } if(x == m-1 && y == n-1) { tmp.push_back({x,y}); arrival = true; return; } tmp.push_back({x,y}); visited[x][y] = true; dfs(obstacleGrid,x,y+1,m,n);//向右 dfs(obstacleGrid,x+1,y,m,n);//向下 // visited[x][y] = false;//写这个会导致时间超时 if(!arrival) tmp.pop_back(); } vector<vector<int>> pathWithObstacles(vector<vector<int>>& obstacleGrid) { int m = obstacleGrid.size(), n = obstacleGrid[0].size(); visited.resize(m,vector<bool>(n,false)); dfs(obstacleGrid,0,0,m,n); return tmp; } };
4、dfs+拓扑排序
- 拓扑排序:在有向图中所有的指向都是一个方向,如果其中有一个指向方向是反的就会构成环,就不是拓扑排序了。
- 题目链接:课程表
class Solution { public: vector<bool>visited; vector<bool>path; bool hasCycle = false; bool canFinish(int numCourses,vector<vector<int>>&prerequisites) { visited.resize(numCourses,false); path.resize(numCourses); vector<vector<int>>graph = buildgraph(prerequisites,numCourses); //for循环是因为可能可以从其他点出发遍历完图,而不是一个固定的开始点 for(int i = 0; i < numCourses; i++) { transfer(graph,i); } return hasCycle ? false : true; } void transfer(vector<vector<int>>&graph,int n) { if(path[n]) { hasCycle = true; return; } if(visited[n] || hasCycle) { return; } visited[n] = true;//这个是为了不重复每次开始遍历的起始点 path[n] = true; for(auto tmp:graph[n]) { transfer(graph,tmp); } //path是为了在这个路径上不重复遍历同一个点 path[n] = false; } vector<vector<int>>buildgraph(vector<vector<int>>&prerequisites,int numCourses) { vector<vector<int>>graph(numCourses); for(auto tmp:prerequisites) { int from = tmp[1]; int to = tmp[0]; graph[from].push_back(to); } return graph; } };
五、广度搜索(BFS,时间复杂度比DFS低)
1、bfs+最短或最优的路径规划
- 这种一把都是不带权值的,然后路径上会有障碍啥的,问你最优的步骤或者次数,这种就相当于可以当作求树的最小深度。带权值的一般就是用dfs做。
- 题目链接:最优路径
class Solution { public: int minstep = INT_MAX;//先设置一个最大移动步数 typedef pair<int,int>PII; vector<vector<int>>visited;//是否已经走过该点 //上下左右 vector<int>posx{0,0,-1,1}; vector<int>posy{-1,1,0,0}; void bfs(vector<vector<char>>&maze,vector<int>&entrance) { int m = maze.size(), n = maze[0].size(); visited.resize(m,vector<int>(n,0)); queue<PII>q; q.push({entrance[0],entrance[1]});//压入其实坐标 while(!q.empty()) { //弹出该点并扩展它的上下左右四个点 int x = q.front().first; int y = q.front().second; q.pop(); //找到目标点,结束 if((x == 0 && (x != entrance[0] || y != entrance[1])) \ || (x == m-1 && (x != entrance[0] || y != entrance[1]))\ || (y == 0 && (x != entrance[0] || y != entrance[1]))\ || (y == n-1 && (x != entrance[0] || y != entrance[1])) ) { minstep = min(minstep,visited[x][y]); break; } //扩展上下左右四个点 for(int i = 0; i < 4; i++) { int nx = x + posx[i]; int ny = y + posy[i]; //满足if条件的点才能被压入队列 if(nx >= 0 && ny >= 0 && nx < m && ny < n && !visited[nx][ny] && maze[nx][ny] != '+') { q.push({nx,ny}); visited[nx][ny] = visited[x][y]+1; } } } } int nearestExit(vector<vector<char>>& maze, vector<int>& entrance) { bfs(maze,entrance); return minstep == INT_MAX ? -1 : minstep; } }; - 带权重的求权重最小或者最大的路径,可以用动态规划来解决,但同时也是下面bfs+dijkstra算法的目标问题。但权重不能是负的。
2、bfs+dijkstra(求单源最短路径)
- 注意,看到最短路径可能就是bfs了,但bfs求最短路径一般是适用于权重为1的,但权重不为1的话就要考虑迪杰斯特拉了。
- 题目链接:最小路径和
class Solution{ public: struct State{ int x,y,pathFromStart; bool operator>(const State& other) { return pathFromStart > other.pathFromStart; } }; //开始这个&没加上,导致最后一个用例超出时间限制,细节,要不然每次都是值传递,设计拷贝构造函数生成临时拷贝,然后又调用析构函数,很花费时间,但是引用的话就不需要了 vector<vector<int>>adj(vector<vector<int>>&grid,int curX,int curY) { int m = grid.size(), n = grid[0].size(); vector<vector<int>>ret; if(curX < m-1) { ret.push_back({curX+1,curY}); } if(curY < n-1) { ret.push_back({curX,curY+1}); } return ret; } int minPathSum(vector<vector<int>>&grid) { int m = grid.size(), n = grid[0].size(); vector<vector<int>>effortTo(m,vector<int>(n,INT_MAX)); effortTo[0][0] = grid[0][0]; priority_queue<State,vector<State>,greater<State>>pq;//优先队列,使得每次出来的都是距离 pq.push(State{0,0,grid[0][0]}); while(!pq.empty()) { State curState = pq.top(); pq.pop(); int curX = curState.x; int curY = curState.y; int curPathFromStart = curState.pathFromStart; if(curX == m-1 && curY == n-1) { return curPathFromStart; } if(curPathFromStart > effortTo[curX][curY]) { continue; } for(vector<int>&neighbor:adj(grid,curX,curY)) { int nextX = neighbor[0]; int nextY = neighbor[1]; int pathToNextNode = grid[nextX][nextY] + effortTo[curX][curY]; if(effortTo[nextX][nextY] > pathToNextNode) { effortTo[nextX][nextY] = pathToNextNode; pq.push(State{nextX,nextY,pathToNextNode}); } } } return -1; } };
六、单调栈
- 求一组数组里每个元素右边第一个大于它的数
- 题目链接:单调栈
class Solution{ public: stack<int>st; vector<int>ret; vector<int> nextGreaterElement(vector<int>& nums) { int n = nums.size(); ret.resize(n); for(int i = n-1; i >= 0; i--) { while(!st.empty() && nums[i] > st.top()) { st.pop(); } ret[i] = st.empty() ? -1 : st.top(); st.push(nums[i]); } return ret; } };
七、滑动窗口
- 滑动窗口一般用来求解某个字符串里面最长的不重复字符串,或者某个字符串包含某个字符串的排列,这种用滑动窗口来解决。模板基本是固定的,如果不是匹配的话就不需要哈希表。
- 题目链接:判断字符串s1是否包含字符串s2
//在s2中找s1 class Solution{ public: bool checkInclusion(string s1,string s2) { unordered_map<char,int>need,window; for(auto c:s1) { need[c]++; } int left = 0, right = 0;//维护窗口的指针 int valid = 0; int n = s1.size();//相当于固定的窗口大小 while(right < s2.length()) { char s = s2[right]; right++; if(need.count(s)) { window[s]++; if(window[s] == need[s]) { valid++; } } //滑动窗口是否超了范围 while(right - left >= n) { if(valid == need.size()) { return true; } char d = s2[left]; left++; if(need.count(d)) { if(need[d] == window[d]) { valid--; } } window[d]--; } } return false; } };
八、单调队列
- 单调队列一般用来求解一个滑动窗口在数组中滑行,每次滑行窗口中的最值。
- 滑动窗口的最大值
class Maxwindow{ deque<int>dq; void push(int n) { while(!dq.empty() && dq.back() < n) { dq.pop(); } dq.push(n); } int maxnum() { return dq.front(); } void pop(int n) { if(n == dq.front()) { dq.pop_front(); } } }; class Solution{ public: vector<int> maxSlidingWindow(vector<int>& nums, int k) { Maxwindow window; int n = nums.size(); vector<int>res; for(int i = 0; i < n; i++) { if(i < k-1) { window.push(nums[i]); } else { window.push(nums[i]); res.push_back(window.max()); window.pop(nums[i-k]); } } } };
九、基础图算法
1、并查集+kruskal(最小生成树)
- 并查集:一般是查找两个节点的父节点是否相同,不相同的话就可以进行合并。
- 克鲁斯卡尔:按照每条边的权重大小排序,依次用并查集构成整个连通图并且没有环。
- 一般解决的题型是将整个图连通并且使得所有边权重和最小。
- 题目链接:最小生成树
class Solution{ public: static bool cmp(const vector<int>& x,const vector<int>& y) { return x[2] < y[2]; } int find(vector<int>&parent,int x) { if(parent[x] != x) { parent[x] = find(parent,parent[x]); } return parent[x]; } int miniSpanningTree(int n,int m,vector<vector<int>>& cost) { vector<int>parent(n+1); for(int i = 0; i <= n; i++) { parent[i] = i; } sort(cost.begin(),cost.end(),cmp); int res = 0; for(int i = 0; i < m; i++) { int x = cost[i][0]; int y = cost[i][1]; int z = cost[i][2]; int px = find(parent,x); int py = find(parent,y); if(py != px) { res += z; parent[px] = py; } } return res; } };