这篇文章我们来看一下数据结构中的二叉搜索树。
目录
1.概述
2.二叉搜索树的实现
3.总结
1.概述
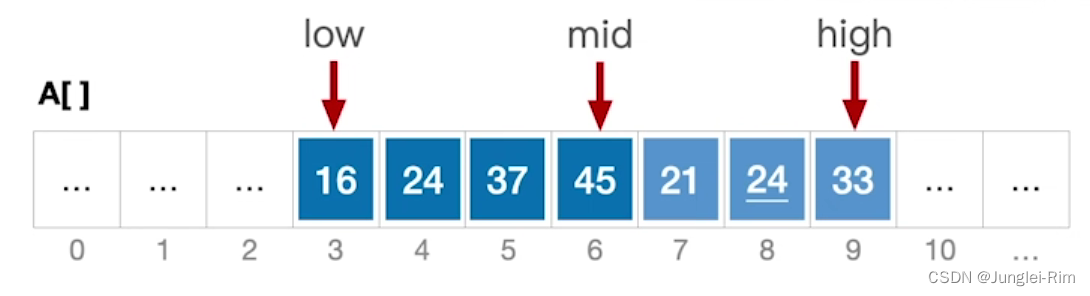
我们前面学到的数据结构,比如:动态数组、链表、队列、栈、堆,这些数据结构存储完数据后,我们要去查找某个数据,它的时间复杂度是O(n),因为这些数据结构的底层实现都是数组或者链表,都是线性的。我们前面有学过二分查找,它的最优时间复杂度为O(lngn)。下面,我们来学习另外一种便于查找的数据结构——二叉搜索树。
二叉搜索树:又被称为二叉查找树。其特点如下:
- 树节点上增加key属性,用来比较谁大谁小,key不可以重复
- 对于任意一个树节点,它的key比它的左子树的key都大,比它的右子树的key都小
下面看一张图:

二叉搜索树的理想查找时间复杂度为O(logn)
2.二叉搜索树的实现
下面来看一下二叉搜索树的实现:
二叉搜索树的根据key值找节点值,找最大,找最小,找前驱和后继都是比较简单的,思路都是很好理解的。
下面重点来讲一下删除的思路(删除的情况很多):
- 删除节点没有左孩子,将右孩子托孤给Parent
- 删除节点没有右孩子,将左孩于托孤给Parent
- 删除节点左右孩子都没有,已经被涵盖在情况1、情况2当中,把null 托孤给Parent
- 删除节点左右孩子都有,可以将它的后继节点(称为S)托孤给Parent,再称S的父亲为SP,又分两种情况:(1)SP就是被删除节点,此时D与S紧邻,只需将S托孤给Parent (2)SP不是被删除节点,此时D与S不相邻,此时需要将S的后代托孤给SP,再将S托孤给Parent
下面来看一下代码的具体实现(代码太长,就不截图展示了):
package Tree;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
/**二叉搜索树*/
public class L2_BSTree1<T extends Comparable<T>> {
/**节点类*/
static class BSTNode<T>{
T key;
Object value;
BSTNode left;
BSTNode right;
public BSTNode(T key) {
this.key = key;
}
public BSTNode(T key, Object value) {
this.key = key;
this.value = value;
}
public BSTNode(T key, Object value, BSTNode left, BSTNode right) {
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
}
BSTNode<T> root;//根节点
/**根据key值得到节点的值*/
public Object get(T key){
BSTNode<T> node = root;
while (node!=null){
/**
* 该值比传入参数大,返回1
* 该值比传入参数小,返回-1
* 该值等于传入参数,返回0
* */
int result = key.compareTo(node.key);
if (result < 0){
node = node.left;
}else if (result > 0){
node = node.right;
}else {
return node.value;
}
}
return null;
}
public Object get1(T key){
return doGet(root,key);
}
private Object doGet(BSTNode<T> node, T key){//递归的函数
int result = key.compareTo(node.key);
if (node == null){
return null;
}
if (result < 0){
return doGet(node.left,key);//向左找
}
else if (result > 0){
return doGet(node.right,key);//向左找
}
else{
return node.value;//返回当前的值
}
}
/**得到最小key值所对应的值*/
public Object min(){//非递归版
return max(root);
}
public Object min(BSTNode node){//非递归版
if (node == null){
return null;
}
BSTNode pre = node;
while (pre.left != null){
pre = pre.left;
}
return pre.value;
}
public Object min1(){//递归版
return doMin(root);
}
private Object doMin(BSTNode node){
if (node == null){
return null;
}
if (node.left == null){
return node.value;
}
return doMin(node.left);
}
/**得到最大key值所对应的值*/
public Object max(){//非递归版
return max(root);
}
private Object max(BSTNode<T> node){
if (node == null){
return null;
}
BSTNode pre = node;
while (pre.right != null){
pre = pre.right;
}
return pre.value;
}
public Object max1(){//递归版
return doMax(root);
}
private Object doMax(BSTNode node){
if (node == null){
return null;
}
if (node.right == null){
return node.value;
}
return doMin(node.right);
}
/**存储key值和节点值*/
public void put(T key,Object value){
//1.如果key存在,更新操作
//1.如果key不存在,新增操作
BSTNode<T> node = root;
BSTNode<T> parent = null;//记录key的前一个值
while (node != null){
parent = node;
int result = key.compareTo(node.key);
if (result < 0){
node = node.left;
}else if (result > 0){
node = node.right;
}else {//找到了
node.value = value;
return;
}
}
//没找到,新增
if (parent == null){
root = new BSTNode<T>(key,value);
}
int result = key.compareTo(parent.key);
if (result < 0){
parent.left = new BSTNode<T>(key,value);
}else if(result > 0){
parent.right = new BSTNode<T>(key,value);
}
}
/**找到某一个key的前驱值*/
public Object predecessor(T key){
BSTNode<T> p = root;
BSTNode<T> ancestorFromLeft = null;
while (p != null){
int result = key.compareTo(p.key);
if (result < 0){
p = p.left;
}else if (result > 0){
ancestorFromLeft = p;
p = p.right;
}else {
break;
}
}
if (p == null){//没找到节点的情况
return null;
}
if (p.left != null){//找到节点,有左子树
return max(p.left);
}
return ancestorFromLeft != null ?
ancestorFromLeft.value :null;
}
/**找到某一个key的后继值*/
public Object successor(T key){
BSTNode<T> p = root;
BSTNode<T> ancestorFromRight = null;
while (p != null){
int result = key.compareTo(p.key);
if (result < 0){
ancestorFromRight = p;
p = p.left;
}else if (result > 0){
p = p.right;
}else {
break;
}
}
if (p == null){//没找到节点的情况
return null;
}
if (p.right != null){//找到节点,有左子树
return min(p.right);
}
return ancestorFromRight != null ?
ancestorFromRight.value :null;
}
/**根据key值删除对应的节点*/
public Object delete(T key){
BSTNode<T> p = root;
BSTNode<T> parent = null;
while (p != null){
int result = key.compareTo(p.key);
if (result < 0){
parent = p;//记录当前节点的父节点
p = p.left;
}else if (result > 0){
parent = p;
p = p.right;
}else {
break;
}
}
if (p == null){
return null;
}
//删除操作
if (p.left == null ){
//情况1
shift(parent,p,p.right);
} else if(p.right == null ){
//情况2
shift(parent,p,p.left);
} else {
//情况4
BSTNode<T> s = p.right;
BSTNode<T> sParent = p;//后继结点的父亲
while (s.left != null){
sParent = s;
s = s.left;
}
if (sParent != p){//不相邻
shift(sParent,s,s.right);
s.right = p.right;
}
shift(parent ,p,s);
s.left = p.left;
}
return p.value;
}
/**
* 托孤方法
* parent:被删除节点的父亲
* deleted:被删除节点
* child:被上去的结点
* */
private void shift(BSTNode<T> parent,BSTNode<T> deleted,BSTNode<T> child){
if (parent == null){
root = child;
} else if (deleted == parent.left){
parent.left = child;
}else {
parent.right = child;
}
}
public Object delete1(T key){
ArrayList<Object> Aresult = new ArrayList<>();//保存被删除节点的值
root = doDelete(root,key,Aresult);
return Aresult.isEmpty()? null:Aresult.get(0);
}
private BSTNode<T> doDelete(BSTNode<T> node,T key,ArrayList<Object> Aresult){
//node:递归删除的起点
//返回值:删剩下的孩子节点
if (node == null){
return null;
}
int result = key.compareTo(node.key);
if (result < 0){
node.left = doDelete(node.left,key,Aresult);
return node;
}
if (result > 0){
node.right = doDelete(node.right,key,Aresult);
return node;
}
Aresult.add(node.value);
if (node.left == null){
return node.right;
}
if(node.right == null){
return node.left;
}
BSTNode<T> s = node.right;
while (s.left != null){
s = s.left;
}
s.right = doDelete(node.right,s.key,new ArrayList<>());
s.left = node.left;
return s;
}
/*找比指定key小的所有节点的value值*/
public List<Object> less(T key){
ArrayList<Object> list = new ArrayList<>();
BSTNode<T> p = root;
LinkedList<BSTNode<T>> stack = new LinkedList<>();
while (p != null || !stack.isEmpty()){
if (p != null){
stack.push(p);
p = p.left;
}else {
BSTNode<T> pop = stack.pop();
int result = key.compareTo( pop.key);
if (result < 0 ){
list.add(pop.value);
} else {
break;
}
p = pop.right;
}
}
return list;
}
/*找比指定key小的所有节点的value值*/
public List<Object> greater(T key){
ArrayList<Object> list = new ArrayList<>();
BSTNode<T> p = root;
LinkedList<BSTNode<T>> stack = new LinkedList<>();
while (p != null || !stack.isEmpty()){
if (p != null){
stack.push(p);
p = p.left;
}else {
BSTNode<T> pop = stack.pop();
int result = key.compareTo( pop.key);
if (result > 0 ){
list.add(pop.value);
}
p = pop.right;
}
}
return list;
}
/*找比指定key小的所有节点的value值*/
public List<Object> between(T key1,T key2){
ArrayList<Object> list = new ArrayList<>();
BSTNode<T> p = root;
LinkedList<BSTNode<T>> stack = new LinkedList<>();
while (p != null || !stack.isEmpty()){
if (p != null){
stack.push(p);
p = p.left;
}else {
BSTNode<T> pop = stack.pop();
int result1 = key1.compareTo( pop.key);
int result2 = key2.compareTo( pop.key);
if (result1 > 0 && result2 < 0){
list.add(pop.value);
}else if (result2 > 0){
break;
}
p = pop.right;
}
}
return list;
}
}
3.总结
怎么说呢,二叉搜索树对比前面的二叉树来说,难度确实是上了一个档次。但是,越学数据结构与算法你越会有这样一种感觉:他们的套路都大差不差!二叉搜索树是用链表来实现的,只要心中有图,多画画图,然后熟悉链表的一些操作,熟悉一些循环流程的判断,那么那些操作都能实现出来。如果实现不了,那就再多结合其他的数据结构来想一想。链表的操作主要就是看一些循环流程的控制。其余的没啥难的。对于数组,数组的一些操作要比链表难,因为数组太死了。
我之前的代码的注释比较多,因为刚接触,不熟悉,但现在代码中的注释并不多,那是因为一些操作都写了很多遍了。虽然不至于能默写下来,但是可以自己推导着写出来。思路有了,也练了几遍手,那么再遇见这个问题自己就能推导了。所以数据结构与算法学到后面主要就是学思路了。