1.归并操作

归并:把两个或多个已经有序的序列合并成一个。

1. 2路归并：二合一
2. k路归并：k合一
3. 结论:m路归并，每选出一个元素需要对比关键字m-1次。

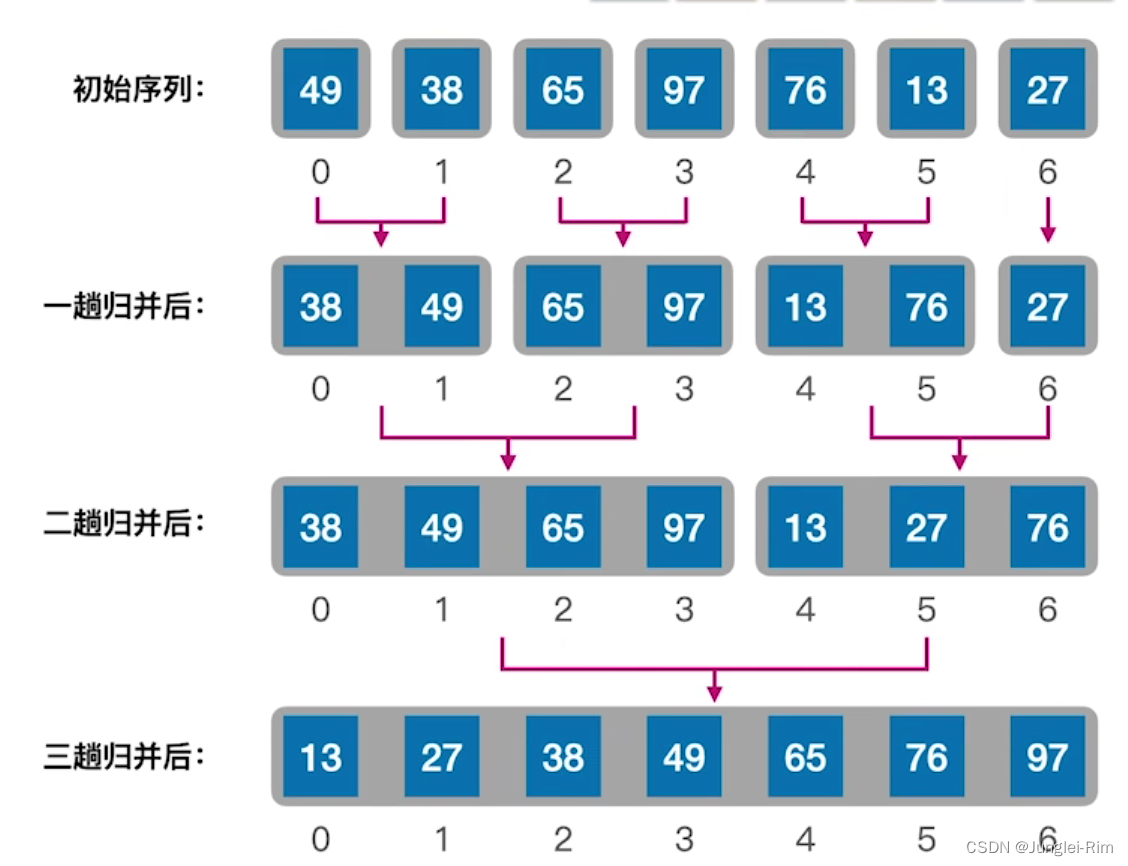
2.算法思想

核心操作:把数组内的两个有序序列归并为一个。
例如：

3.代码实现

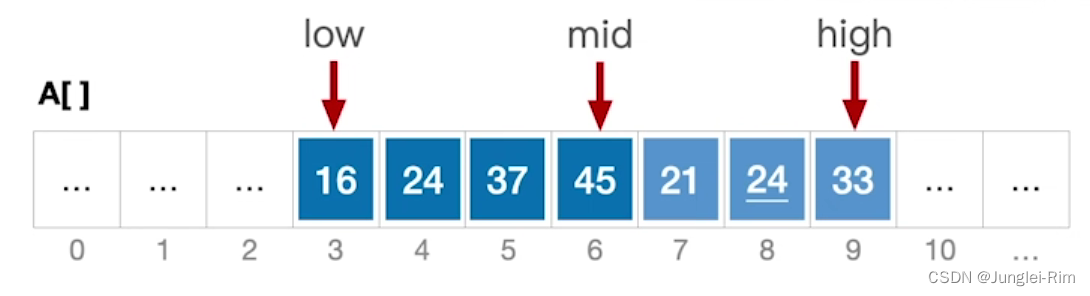
将一个数组分为两个有序序列：

• low指针指向第一个序列的首位元素，
• mid指针指向第一个序列的末位元素，
• high指针指向第二个序列的末位元素。

1.排序过程

1. 若low<high，则将序列分从中间mid=(low+high)/2分开
2. 对左半部分[low, mid]递归地进行归并排序
3. 对右半部分[mid+1, high]递归地进行归并排序
4. 将左右两个有序子序列Merge为一个
   

2.具体代码

int *B = (int *) malloc(n * sizeof(int)); //辅助数组B

//A[ low...mid ]和A[ mid+1...high]各自有序，将两个部分归并
void Merge(int A[], int low, int mid, int high) {
    int i, j, k;
    for (k = low; k <= high; k++)
        B[k] = A[k];//将A中所有元素复制到B中
    for (i = low, j = mid + 1, k = i; i <= mid && j <= high; k++) {
        if (B[i] <= B[j])
            A[k] = B[i++];//将较小值复制到A中
        else
            A[k] = B[j++];
    }
    while (i <= mid)A[k++] = B[i++];
    while (j <= high)A[k++] = B[j++];
}

void MergeSort(int A[], int low, int high) {
    if (low < high) {
        int mid = (low + high) / 2;//从中间划分
        MergeSort(A, low, mid);//对左半部分归并排序
        MergeSort(A, mid + 1, high);//对右半部分归方p序
        Merge(A, low, mid, high); //归并
    }
}

4.算法效率分析

2路归并的“归并树”：形态上就是一棵倒立的二叉树。

1.时间复杂度

• 二叉树的第h层最多有$2^h-1$个结点若树高为h，则应满足$n<=2^h-1$。
• 即$h-1=[lo{g}_{2}n](向上取整)$
• 结论:n个元素进行2路归并排序，归并趟数=$[lo{g}_{2}n](向上取整)$
• 每趟归并时间复杂度为O(n)，则算法时间复杂度为$O(nlo{g}_{2}n)$。

2.空间复杂度

空间复杂度=O(n)，来自于辅助数组B.

3.稳定性

当左右两边的关键字相同是，优先让靠左边的关键字归并，所有说是稳定的。